深入求解2019年高考全国卷中的两道解三角形题
2020-04-01 04:15甘志国
数理化解题研究 2020年10期
甘志国
(北京市丰台二中 100071)
解三角形问题,往往需要用正弦定理“边化角”或“角化边”,而在很多时候并不是两条路都行得通,但如果做深入思考,两条路都是行得通的.解三角形问题,难点是对求得的结果进行检验(舍取),比如2013年高考北京卷理科数学第15(2)题.
下面将深入求解2019年高考全国卷中的两道解三角形题,领略解三角形的神秘莫测.
题1 (2019年高考全国卷Ⅰ理科第17题)△ABC的内角A,B,C的对边分别为a,b,c,设(sinB-sinC)2=sin2A-sinBsinC.
(1)求A;
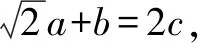
解(1)由题设可得sin2B+sin2C-sin2A=sinBsinC,再由正弦定理可得b2+c2-a2=bc.
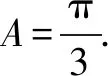
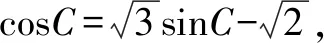
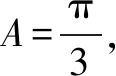
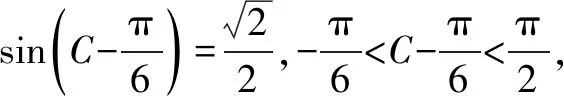
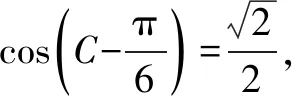
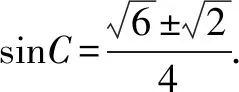
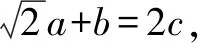
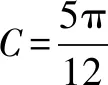
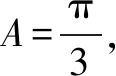
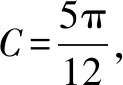
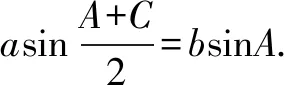
(1)求B;
(2)若△ABC为锐角三角形,且c=1,求△ABC面积的取值范围.
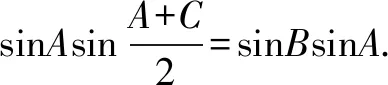
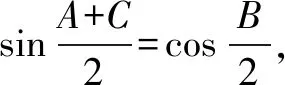
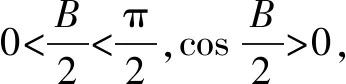
(2)由题设及(1)的答案可得△ABC的面积
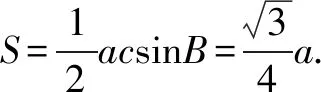
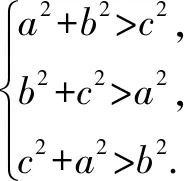
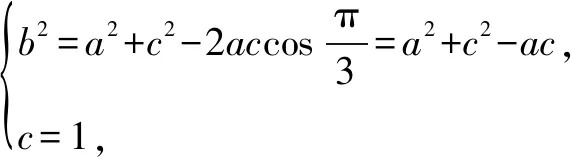
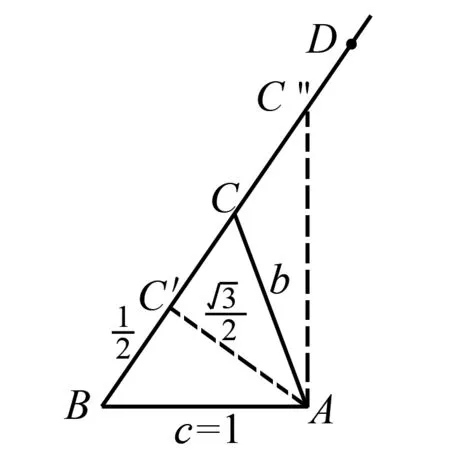
图1
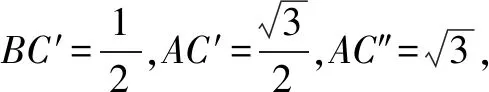
猜你喜欢
风流一代·青春(2022年3期)2022-03-19
中等数学(2021年9期)2021-11-22
中等数学(2021年8期)2021-11-22
北方人(2021年8期)2021-09-03
北方人(2021年15期)2021-08-26
河北理科教学研究(2021年1期)2021-06-07
语数外学习·初中版(2020年6期)2020-09-10
数理化解题研究(2020年4期)2020-03-02
新高考·英语基础(高一)(2019年1期)2019-06-25
新高考·高二数学(2018年1期)2018-11-20

