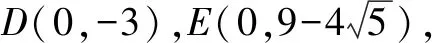由含参二次函数零点分布引发的二元范围问题的思考

沈海全

(浙江省绍兴市越州中学 312000)

一、问题呈现

问题(2017浙江高考样卷)已知函数f(x)=x2+ax+b在x∈(-1,2)上有两个不同的零点，则a+b的取值范围.

本题以含参二次函数为背景，通过在给定范围内的零点问题来限定参数的范围.背景简单，起点低，视角宽，思想丰富，可探究性强，具有很好的学习、观摩、研究的价值.

二、问题解法

视角一(规划问题视角)记z=a+b.

根据零点分布可得以下约束条件

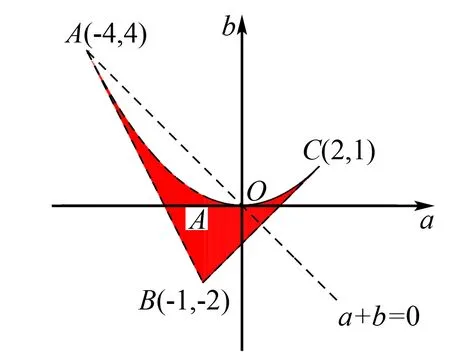
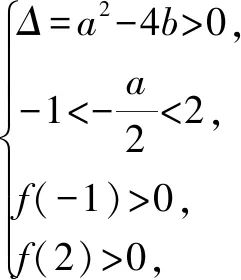
评注根据二次函数根的分布写出约束条件作出可行域，进而从规划的视角解决此类问题是通法，学生容易想到，而且可以解决更一般的线性目标函数如z=ma+nb的最值问题.

视角二(函数值视角)

因为f(x)=x2+ax+b=(x-x1)(x-x2)，且x1,x2∈(-1,2)，又a+b=f(1)-1，而f(1)=(1-x1)(1-x2)∈(-2,4)，则a+b∈(-3,3).

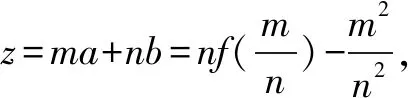
视角三(根与系数视角)

因为x1+x2=-a,x1·x2=b，则a+b=-(x1+x2)+x1·x2=(x1-1)(x2-1)-1，后面同上.

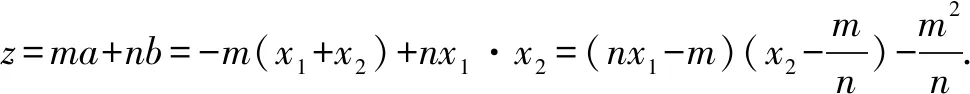
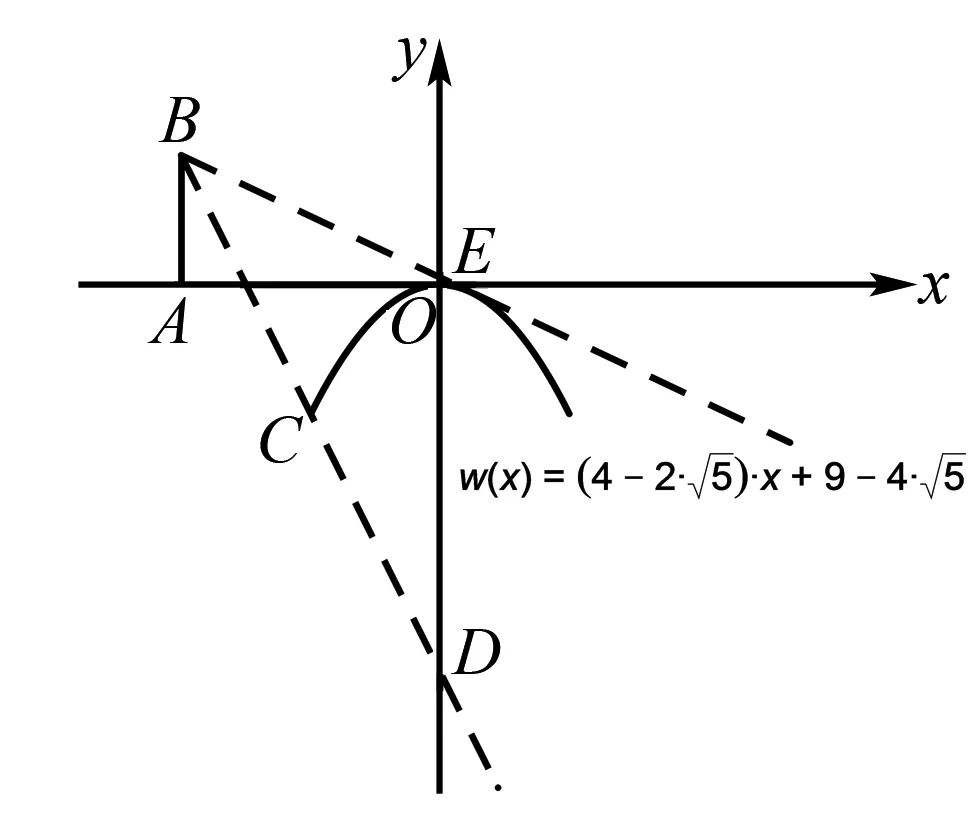
视角四(函数拆分数形结合视角)

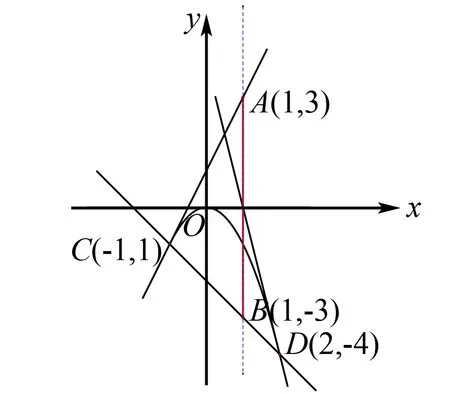
函数f(x)=x2+ax+b在x∈(-1,2)上有个不同的零点⟺方程-x2=ax+b在x∈(-1,2)上有两解⟺函数g(x)=-x2与函数h(x)=ax+b图象有两个交点. 而a+b=h(1).结合图象分析当h(x)过C(-1,-1)，D(2,-4)时h(1)取到最小值，当h(x)与f(x)相切于C(-1,-1)时h(1)取到最大值.综上h(1)为线段AB上的点的纵坐标，可得a+b=h(1)∈(-3,3).

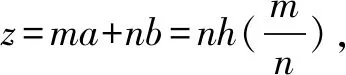
三、变式拓展

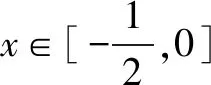
视角一(规划问题视角)

限于篇幅不再给出解答，但变式为有零点问题后约束条件需分一个零点和两个零点讨论，显得稍麻烦，但仍是解决线性目标函数的通法.

视角二(函数值视角)

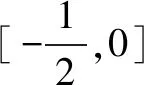
综上a-2b∈[0,1].

评注在上题视角二的基础上进行了改进，巧妙地将a,b用f(1)和r来表示，再利用f(1)和r范围求出a-2b的取值范围，同样可以解决更为一般的线性目标函数.

视角三(根与系数视角)

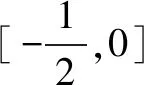
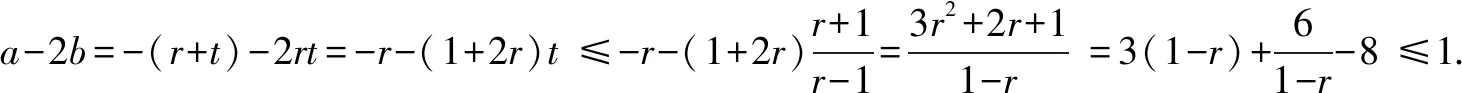
综上a-2b∈[0,1].

评注在上题视角三的基础上进行了改进，利用根与系数的关系，再结合a+b的范围，表示出r,t间的不等关系，再利用r范围求出a-2b的取值范围，同样可以解决更为一般的线性目标函数.

视角四(函数拆分数形结合视角)

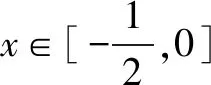
评注函数拆分数形结合的视角将约束条件0≤a+b≤1转化为h(x)=ax+b必须与线段AB有交点，且与g(x)=-x2有交点即可，数形结合显得非常经典，简洁又易懂.

四、链接高考

(2015浙江文科最后压轴题第20题)设函数f(x)=x2+ax+b.

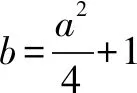
(2)已知函数f(x)在[-1,1]上存在零点，0≤b-2a≤1，求b的取值范围.

解(1)略.函数f(x)=x2+ax+b.

(2)仅从函数拆分数形结合视角入手.