取对数与去对数符号显威力
2020-04-01 04:15杜红全
数理化解题研究 2020年10期
杜红全
(甘肃省康县教育局教研室 746500)
所谓取对数就是把不含对数符号的等式转化为含有对数符号的等式,即设x、y、a均为正数,且a≠1,若x=y,则logax=logay;所谓去对数就是把同底数的两个相等的对数式子转化为不含对数符号的等式,即设x、y、a均为正数,且a≠1,若logax=logay,则x=y.在化简、计算、求值、证明中,若能巧妙地运用取对数与去对数符号的方法,则使问题简单化.现举例说明.
一、取对数
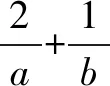
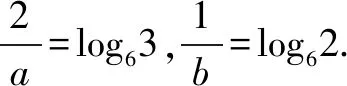
例2 解方程6x+2=2x+3·33x.
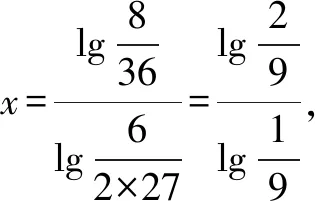
二、去对数符号
例3 解方程lg(x2+11x+8)-lg(x+1)=1.
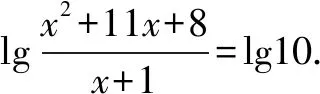
检验:x=-2时,x+1<0,负数的对数无意义,所以x=-2不是原方程的根;x=1时,原方程左边=lg20-lg2=lg10=1=右边.
所以x=1是原方程的根.
例4 已知a、b、c是△ABC的三条边,且方程x2-2x+lg(c2-b2)-2lga+1=0有等根,求证:△ABC是直角三角形.
证明因为方程x2-2x+lg(c2-b2)-2lga+1=0有等根,所以△=4-4lg(c2-b2)+8lga-4=0,即lg(c2-b2)=lga2.
所以c2-b2=a2,即a2+b2=c2.
所以△ABC是直角三角形.
三、取对数与去对数符号同时应用
例5 设ax=by=cz,且x-1+y-1=z-1,求证:ab=c.
分析应该把指数式转化为对数式,将x、y、z分离出来.
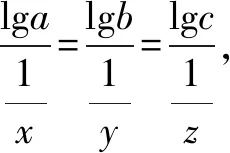
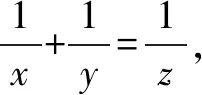
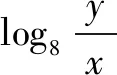
解根据对数的运算法则,原等式可化为
loga[(x2+4)·(y2+1)]=loga[5(2xy-1)],所以(x2+4)(y2+1)=5(2xy-1).
整理,得x2y2+x2+4y2-10xy+9=0.
配方得(xy-3)2+(x-2y)2=0.
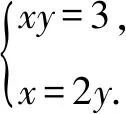
猜你喜欢
小学生学习指导(高年级)(2022年10期)2022-11-04
中学生数理化·中考版(2021年9期)2021-11-20
小学生学习指导(高年级)(2021年10期)2021-11-02
中学生数理化·七年级数学人教版(2020年11期)2020-12-14
中学生数理化·七年级数学人教版(2019年9期)2019-11-25
中学生数理化·七年级数学人教版(2017年3期)2018-01-20
中学生数理化·中考版(2017年9期)2017-12-20
中学生数理化·七年级数学人教版(2017年12期)2017-02-15
中学生数理化·七年级数学人教版(2017年12期)2017-02-15
中学生数理化·七年级数学人教版(2016年8期)2016-12-07

