基于车头时距与行程时间的排队长度算法*

龚方徽 朱海峰 温熙华 刘彦斌

(中电海康集团研究院 杭州 310012)

信号交叉口排队长度是城市交通信号控制的重要参数之一，也是评估交叉口放行效率的重要依据。传统排队长度建模方法一般基于交通波理论、排队论方法，以及累积曲线理论等。交通系统是一个非线性、不连续、时变的复杂系统，无论是传统模型还是基于传统模型的优化模型均无法实时地对排队长度进行准确计算。此类算法不可避免地存在一些不足，例如，模型适用范围受限、部分参数在实际工程应用中难以获得等问题。

随着科技的进步，交通检测数据日益多元化，近年来学者们以数据为新角度提出一系列排队长度算法。通过实时道路监控视频图像序列，利用帧间差判断车辆是否排队，从而计算排队长度[1]。采用线圈检测数据确定排队队尾车辆[2]，以及利用浮动车数据估算交叉口排队长度[3-4]。一般情况下使用浮动车数据的算法精度依赖于浮动车所占比例大小。基于地磁传感器，利用车辆通过传感器时间及车尾时距的动态变化规律，进行排队长度估计[5]，但此方法无法适用于排队过饱和的情况。利用视频检测数据提出基于车辆延误时间的交叉口交通状态判别划分，并设计欠饱和及饱和状态下的交叉口排队长度算法，该方法在2种交通状态下均需使用上下游过车时间[6-7]。

基于电警过车数据，本文通过分析车辆通过进口道检测器的车头时距动态变化规律，分析本周期最大排队长度。同时，针对多次排队、交叉口间绿波协调情况，结合驶离车辆行程时间，设计相应计算方法对排队长度值进行修正。

1 排队长度计算

排队长度指绿灯初始时刻，进口道停车线与最后一辆停止车辆间的距离，可用排队车辆数与有效车辆长度的乘积代替。当绿灯启亮后，排队车辆通过停车线时，两辆车之间的车头时距存在规律性，即排队车辆一般以稳定、紧凑的车头时距通过交叉口，而非排队车辆之间的车头时距为非紧凑、离散的状态。故可以通过车头时距数值的变化来识别排队车辆，发生离散的数值对应的车辆即为非排队车辆首车。

截取绿灯时长范围[Tstart，Tend]内过车数据集合{Noi，Timei}，其中：Noi为车牌号；Timei为车辆Noi通过本车道的时间,s。根据各个车辆过车时刻计算车头时距值集合{ht,i}，其中

ht,1=Time1-Tstart

(1)

ht,i=Timei-Timei-1,i>1

(2)

最基础的排队模型为：遍历车头时距集合{ht,i}，若存在某车头时距值ht,i大于车头时距阈值δ，则此车头时距对应的车辆Noi为非排队通行车辆的首车，早于车辆Noi驶离的车辆均为本周期本车道排队车辆。排队车辆与通行车辆间的车头时距关系图见图1。

实心圆-排队车辆；空心圆-通行车辆；2圆形之间的距离-车头时距。

若考虑驾驶人员的驾驶习惯等情况，可能会出现某辆排队车辆Nop与上一辆排队车辆的车头时距值较大的情况。此类情况若仅适用上述基础模型会将排队车辆误判为非排队通行车辆。此时应对再下一驶离车辆进行分析，判断该车是否为排队车辆。若下一车头时距值较小，则认为车辆为排队车辆，继续向后搜寻排队尾车；否则认为车辆为非排队车辆。设置多个车头时距阈值δ1,δ2,δ3用以区分排队车辆与非排队通行车辆。其中：δ1>δ2>δ3，依据对历史数据的分析对3个参数赋予经验值。车头时距阈值单位均为s。

遍历车头时距，若车头时距ht,p>δ1，可直接区分排队与非排队通行车辆，车辆Nop为非排队车辆的首车，见图2；若车头时距δ1>ht,p>δ2，则观察下一个车头时距值ht,p+1，若下一车头时距较大，即ht,p+1>δ2，则车辆Nop为非排队车辆的首车，后面车辆均为非排队通行车辆，见图3。

图2 排队情况一

图3 排队情况二

若排队车辆数p-1小于本周期驶离的车辆总数，则排队长度为

Lqueue=Leff×(p-1)

(3)

式中：Leff为有效车辆长度，7 m；Lqueue为排队长度，m。

2 二次排队长度修正

上一节的计算方法仅能计算出欠饱和状态下的排队长度。车道过饱和状态下，路段上会出现车辆进行二次排队的情况，本周期过车数小于排队车辆总数，此时需要进行排队长度修正。

首先，判断是否存在车辆进行二次排队。若存在二次排队车辆，则本周期排队车辆数大于驶离车辆数，且驶离车辆均为排队车辆数。即按上一节算法识别出本周期所有过车均为排队车辆，则可能存在二次排队车辆。二次排队车辆图见图4。图4中第一行表示上一周期排队情况，第二行表示本周期排队情况。虚线前的圆表示本周期放行车辆，方框内实心圆表示经过二次排队放行的车辆。

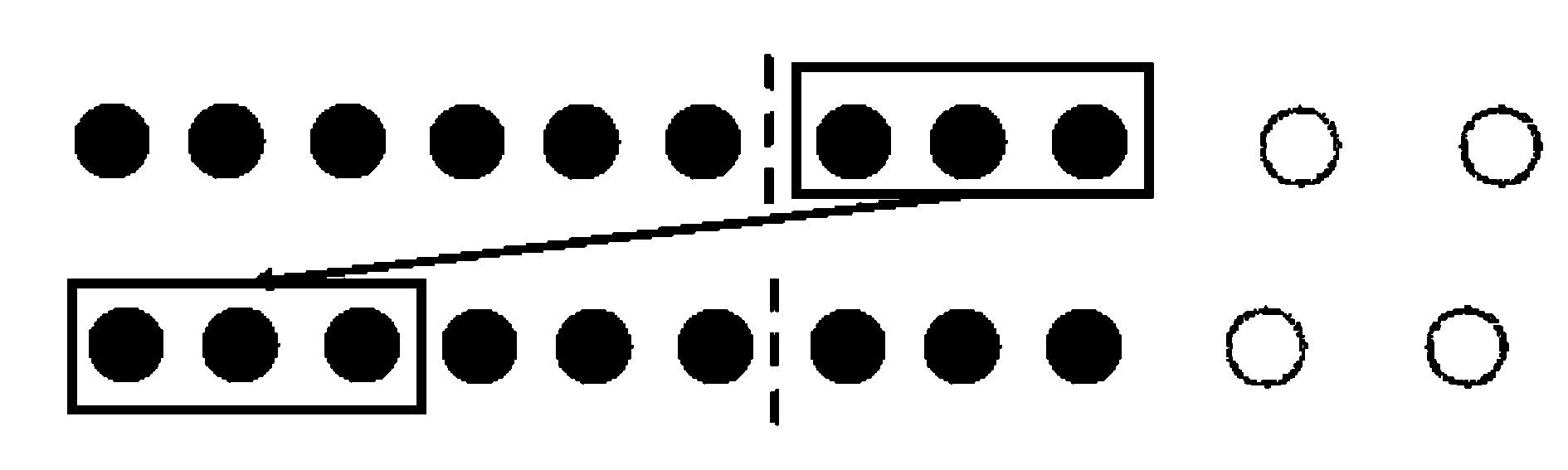
图4 二次排队示意

统计本周期内驶离车辆从上游交叉口至本交叉口的行程时间集合{Tt,i}。分析本周期驶离车辆中仅等待1次红灯的车辆数以及占所有驶离车辆数的比例。若车辆为二次排队车辆，等待时间必大于一周期红灯时长，故车辆行程时间应大于自由流行程时间与红灯时长之和。

设置阈值Ttra用以判断车辆是否进行二次排队。

Ttra=r+Lroad/vfree

(4)

式中：r为本车道对应放行相位的红灯时长，s；Lroad为路段长度，m；vfree为车辆在路段上的自由流速度，m/s。若某车辆Nop的行程时间满足Tt,p>Ttra，则车辆Nop为多次排队车辆。

行程时间集合{Tt,p}中元素个数为N，其中小于Ttra的元素个数为N′，则本周期内一次排队车辆数占总放行车辆数的比例为

η=N′/N

(5)

过饱和情况下相邻2个周期排队车辆总数相距不大，驶离车辆数差距极小。假设上一周期放行车辆数与本周期放行车辆数相同，上一周期排队车辆数为放行车辆数与本周期识别为二次排队车辆数之和。相邻个2周期均为过饱和状态，用上一周期排队车辆数近似本周期排队车辆数。

故本周期本车道排队车辆总数

Qqueue=N+(1-η)N=(2-η)N

(6)

本周期相应的车辆排队长度为

Lqueue=Leff×Qqueue

(7)

对于车辆多次排队的情况，可利用式(8)近似得到本周期排队车辆数。

Qqueue=(m+1-η′)N

(8)

式中：m为放行车辆中最少排队次数；η′为最小排队次数车辆占放行车辆数的比例。

3 绿波路段排队长度修正

若本交叉口与上游交叉口间有绿波协调，则采用本小节方法进行排队长度计算。绿波的目的是使得行驶车辆能够不遇红灯或少遇红灯通过各交叉口。假设车道本周期红灯时间内暂无排队车辆，上游车辆在绿波的作用下到达本交叉口时处于绿灯状态，车辆无需停车驶离本交叉口，此时驶离车辆车头时距序列呈现出与排队车辆车头时距相似的稳定、不离散特征。若车道本周期红灯时间内存在若干排队车辆，绿灯启动，排队车辆消散完时，上游车辆在绿波的作用下正好到达本交叉口，此时所有驶离车辆车头时距与排队车辆呈现相同特征。

若交叉口具有绿波效果，从车头时距数据层面分析，未排队驶离车辆可能会被误判为排队车辆。故需要利用车辆行程时间对暂时计算出来的排队车辆数预估值进行修正。

遍历车头时距集合{ht,i}，当p>1时，若存在某车头时距值ht,p大于阈值δ2(定义同上)，则此车头时距对应的车辆为非排队通行车辆的首车，排队车辆数预估值为p-1。若车头时距值ht,p均小于阈值δ2，则排队车辆预估值为驶离车辆总数。

若车辆未等待红灯，直接通行，则所需要的行程时间为

Tfreepass=Lroad/vfree

(9)

在本周期内排队车辆对应的行程时间集合中，小于等于Tfreepass的元素比例ηfreepass若大于0，则说明至少存在部分的车辆未进行排队，此时可能对排队车辆数误判，需进行排队车辆数修正。

预估排队车辆数应乘以排队通行车辆比例(1-ηfreepass)，得到排队车辆数如式(10)

Qqueue=(1-ηfreepass)×Qqueue

(10)

本周期相应的车辆排队长度为

Lqueue=Leff×Qqueue

(11)

4 算法验证

为验证本算法在真实工程环境的可行性与准确性，通过桐乡市庆丰路沿路各交叉口电警数据对本文方法进行验证，利用视频记录现场排队情况，作为本文算法结果的对比依据。在试验过程中，将小客车、小型货车、公共汽车等各类机动车数量按一定的折算系数换算为标准小汽车当量数。实验结果见表1，表中罗列上游交叉口、下游交叉口、路段实际排队长度、排队长度算法计算值及误差。16组数据中包含绿波协调、车辆二次排队等情况。当车道车辆仅存在一次排队车辆时，实际排队长度值与算法计算值的实际误差在7 m以内，即排队车辆数误差仅为1。存在二次排队车辆情况时，实际排队长度值与算法计算法的相对误差在9.1%左右。

表1 实验结果 m

5 结语

本文提出了一种基于车头时距变化规律的实时计算路段排队长度值的算法。针对车道多次排队、交叉口间绿波协调情况，结合车辆行程时间设计相应计算方法。通过实时监控视频对比计算结果，证明本算法具有较高准确性与实用性。研究成果便于工程实践，可以为优化城市交通信号控制策略提供数据支撑。