考虑斜拉索抗弯刚度的矮塔斜拉桥索导管安装角度修正方法

邓同生 石守鹏

(1.重庆交通大学土木工程学院 重庆 400074； 2.中交二航局第三工程有限公司 镇江 212000)

斜拉索是斜拉桥中的重要受力构件，其耐久性越来越受到人们的重视。影响斜拉索耐久性的因素很多，施工时斜拉索的安装质量对其耐久性的影响很大，若斜拉索安装不当，造成斜拉索与索导管距离太近，则斜拉索在后期极有可能与索导管管壁发生摩擦，使得斜拉索受损，影响斜拉索的使用寿命。

在混凝土斜拉桥中，需要通过预埋索导管为斜拉索预留管道，索导管为直线形，一般由设计图纸说明索导管的安装角度，但该角度是根据塔和梁上的2个锚固点按直线确定的角度，而实际情况下，斜拉索是1条悬链线，其真实线形图见图1。由于这2种线形的差异，所以斜拉索在索导管中无法完全居中，考虑到索导管出口处还需要安装减振装置，因此通常保证在索导管出口处斜拉索居中，而在锚固点处斜拉索并不居中，梁端预埋索导管示意图见图2。

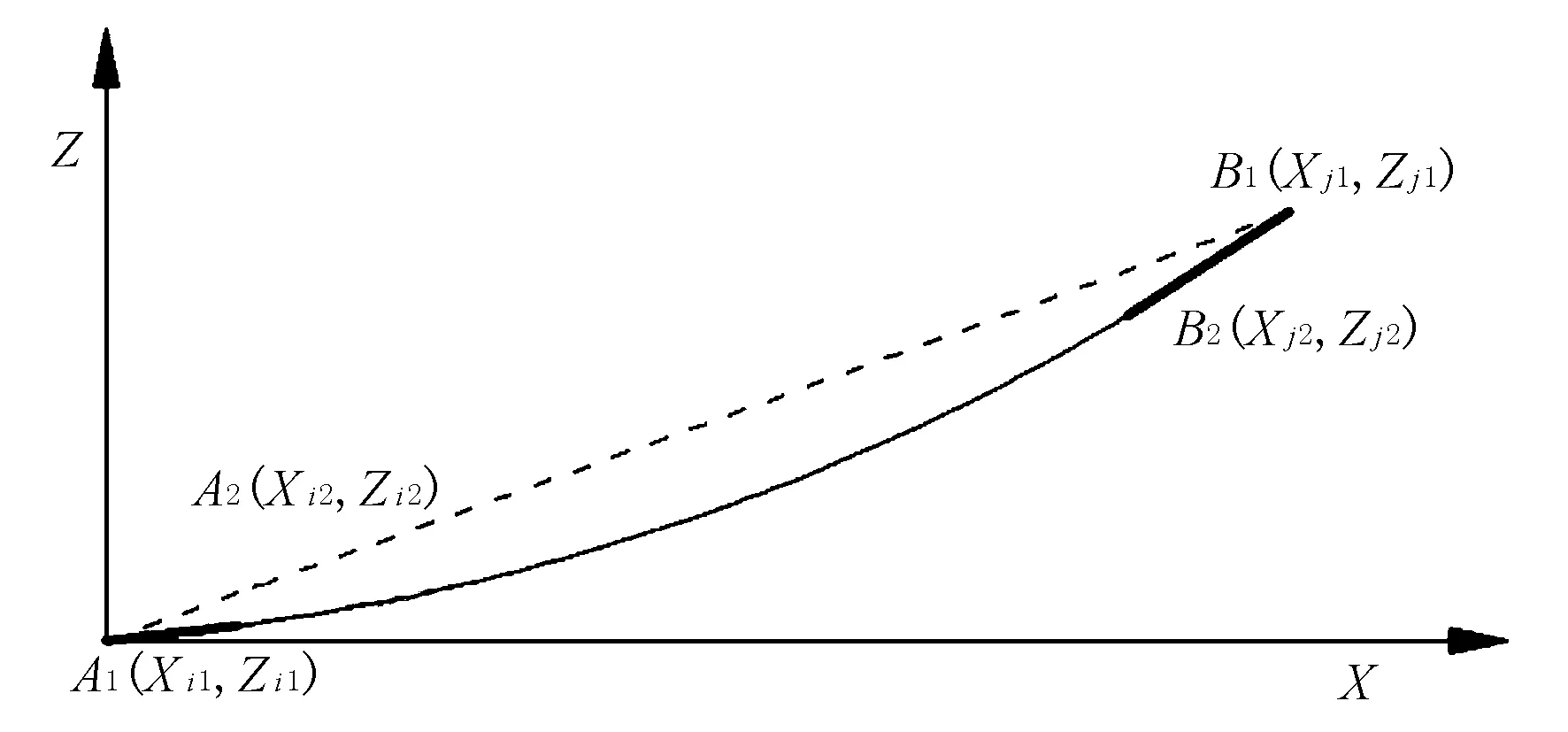
图1 斜拉索自重作用下线形图

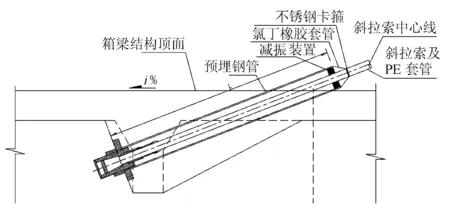
图2 梁端预埋索导管示意图

一般情况下，当索导管长度不长时，2种线形引起的差别并不十分突出，但在矮塔斜拉桥中，主梁高度较大，索导管的长度也较长，此时2种线形之间的差别则较大，在索导管预埋时必须考虑此问题，对预埋索导管安装角度进行修正，避免索导管与斜拉索间发生摩擦。已有学者进行了不少研究，并提出了相应的计算方法。目前提出的计算方法中，通常都将斜拉索看做完全柔性的拉索，进而推导得出相应的计算方法。但矮塔斜拉桥的拉索相对较短，在巨大索力下其横向抗弯刚度不能忽略。本文拟将斜拉索看作1根杆件，考虑斜拉索抗弯刚度，推导拉索两端水平倾角计算方法，并将该方法应用于阿蓬江特大桥以进行验证。

1 常规索导管安装角度修正方法

依据文献[1-2]介绍的整体分析方法，在拉索索力和自重作用下拉索各截面弯矩为0。关心拉索两端约束情况和自重产生的支反力，将斜拉索作为一个整体分析。文献[1]中，在推导拉索塔柱端和主梁端切向角时，拉索两端受力分析采用三角形原理并建立整体平衡方程；文献[2]中则利用对拉索一端取矩建立平衡方程。两者都是将拉索整体分析来建立平衡方程，求解拉索两端切向角。

整体分析方法在实际工程中存在一些误差，施工测定的索力与计算公式所用的设计索力两者虽然数值相同，代表意义却不同，施工实际测定的是斜拉索端部切向索力。以文献[1]为例加以说明，拉索受力分析见图3。

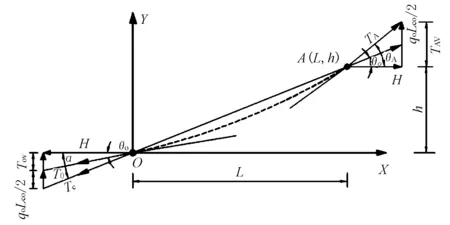
图3 拉索受力分析图

由图3模型推导得到塔柱端和主梁端拉索计算切向角θO、θA为式(1)和(2)[1]。

(1)

(2)

式中：α为弦切线倾角，即拉索设计倾角；qo为斜拉索无应力下自重集度；Lco为斜拉索的原始长度；TO为施工测定斜拉索实际索力；TC为斜拉索弦向力。

实际施工时已知的是与θO有关的TO，然而θO又由TC计算得出。因此，要得到真实TC必须对其进行迭代计算，具体迭代计算这里不做详细说明。

文献[3-4]中介绍了斜拉索微元分析方法，即悬链线理论计算方法。在推导拉索塔柱端和主梁端切向角时取拉索微段进行受力分析，建立平衡微分方程求解斜拉索实际线性。该方法较整体分析方法计算结果略准确。当然，随着计算机的快速发展，也可建立斜拉索有限元模型进行计算分析，这样得到的斜拉索两端切线倾角更加精确。

文献[5]中介绍的计算方法则是将索导管出口中心处与塔端锚固点、梁端锚固点间的拉索看成一条直线，将该直线作为索导管安装方向。安装角度修正计算时，取索导管出口中心处到锚固点长度的拉索进行局部分析，对索导管出口处的拉索中心取距并建立平衡方程，求出索导管出口处拉索偏移量。该方法虽然在建立局部平衡方程上的思路与本文相似，但同样未考虑拉索横向刚度，将拉索各截面弯矩视为0，并且未得到拉索在自重和索力共同作用下的实际线形。

2 考虑斜拉索抗弯刚度的索导管安装角度

由矮塔斜拉桥特点可知，其斜拉索长度较短，自重轻，自重和索力作用下变形较小，在巨大的索力下自身横向抗弯刚度不能忽略，因此，可以将斜拉索看作杆件进行受力分析，考虑拉索各截面弯矩值并建立局部平衡微分方程，求解斜拉索在自重和索力共同作用下的变形。

斜拉索索梁锚固端为坐标原点O，其X轴平行于弦切线指向塔端为正，Y轴以垂直于X轴向下为正，斜拉索局部受力分析见图4。假定①斜拉索抗弯刚度按实际截面计算所得抗弯刚度的2/3取值[6]；②拉索自重作为外力，沿拉索均匀分布；③斜拉索约束视为两端固定铰；④斜拉索弹性模量不考虑垂度和施工中索力变化的影响，不做修正；⑤拉索变形前后重心位置只在竖向发生移动，水平方向坐标不变[7-10]。

硫酸铜溶液在浓缩结晶槽内完成蒸发、冷却结晶之后，边搅拌边用气动双隔膜泵抽取至真空带式过滤机进料口；硫酸铜晶体在带式过滤机上过滤、洗涤、吸干［1］，然后通过埋刮板给料运输机输送至流化床受料斗，进入干燥包装工序。实验数据表明过滤后的硫酸铜含水率在5%～10%，与原过滤器含水5%～9%基本一致，可满足后段工序流化床干燥设备的工艺要求。

(3)

式中：T为斜拉索弦向力，kN；x为斜拉索的原始长度，m；θ为斜拉索弦切线与主梁夹角，(°)；q′ 为变形后拉索自重集度，kN/m；x′为拉索原始长度x变形后的长度，m；E为斜拉索弹性模量，kN/m2；I为斜拉索截面惯性矩，m4。

假设自重和索力共同作用下拉索长度为S,并且变形前后自重集度、单位索长伸长量与拉索变形前后长度的比值呈线性关系，则可得式(4)。

(4)

(5)

结合式(4)、(5)对微分方程(3)进行整理得

B·y″(x)+T·y(x)+C·x2+Dx=0

(6)

(7)

对y(x)关于x求导得

(8)

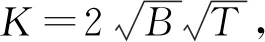
(9)

(10)

当x=L时，同样可以得到斜拉索与主塔形成的夹角β，其中γ=90°-θ。

(11)

3 工程应用

3.1 工程概况

阿蓬江特大桥为客、货两用铁路桥，桥址位于重庆市黔江区舟白镇县坝村，跨越S202省道。其主桥为跨度135 m+240 m+135 m的矮塔斜拉桥，主塔高度为桥面以上34 m，H形结构。斜拉索采用双索面扇形布置，布置在主梁的两侧，全桥设置44对共88根拉索，梁上拉索水平间距7.0 m，塔端斜拉索竖向间距1.2 m，安装时在塔端锚固、主梁端张拉。全桥总体布置图见图5。

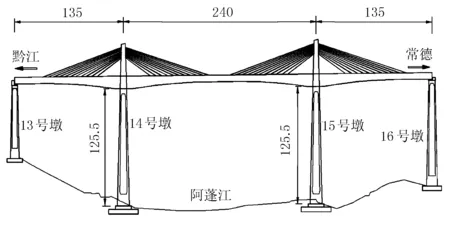
图5 总体布置图(单位：m)

3.2 安装角度修正结果

阿蓬江特大桥主桥的14号、15号塔上各布置22对斜拉索，2塔斜拉索对称布置，其形式和各参数完全相同。以14号塔左侧最短索A1、中间长度索A6、最长索A11及设计索力最大索A94对索为例，根据设计索力对重力作用下垂度引起的斜拉索两端锚固处水平倾角进行修正，变化值计算结果见表1。

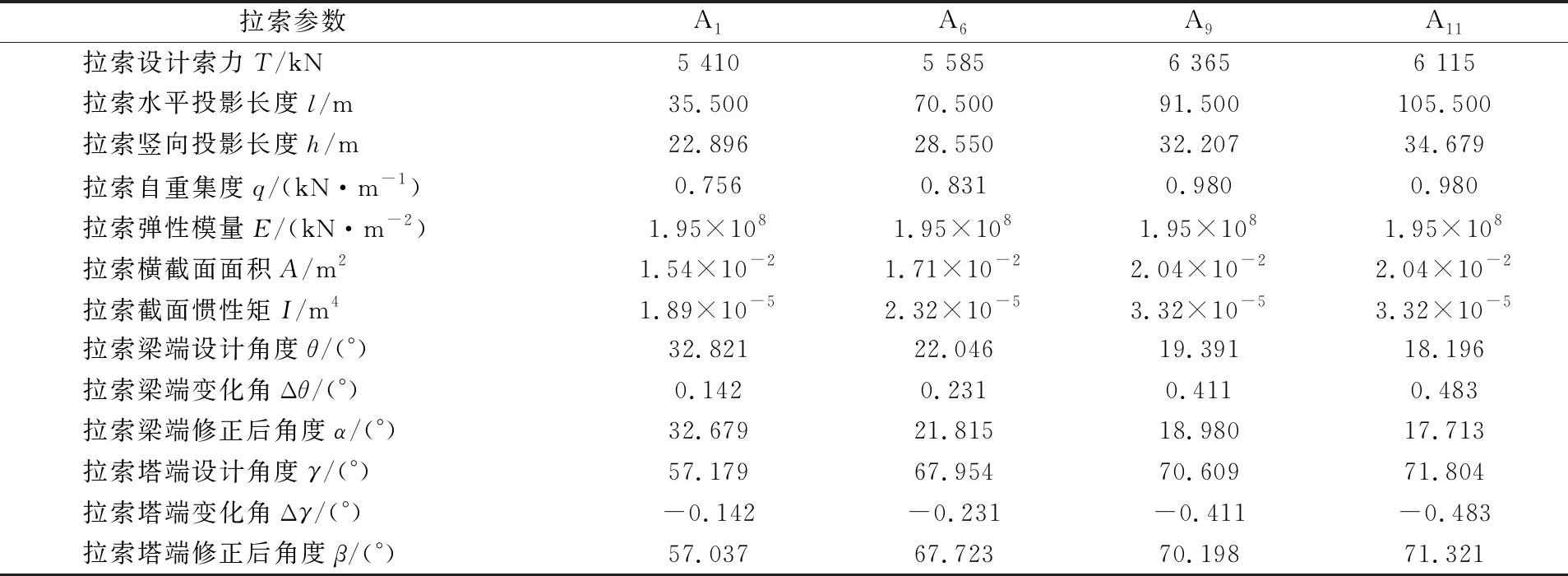
表1 垂度引起的斜拉索水平倾角修正对比

注：θ为斜拉索与主梁形成的夹角；γ为斜拉索与主塔形成的夹角。

由表1可见，垂度引起的斜拉索角度变化值随着索长的增加而变大，其中索A11最大，塔端与梁端均为0.483°。塔端预埋索导管长度为6.899 m，直径为37.7 cm；梁端预埋索导管长度为5.444 m，直径为45 cm。计算出塔端和梁端管口偏移量分别为5.816，4.589 cm，由于索A11直径为16.13 cm，得到垂度影响下斜拉索外缘与索导管内壁的距离分别为4.969，9.846 cm。显然，塔端比梁端更易出现碰管，但是梁端索导管内须安装减震装置，因此，对两端索导管预埋角度进行修正是必要的。

4 各修正方法计算结果对比

为验证本文推导公式的正确性并得到与其他计算方法的差异大小，利用上述不同计算方法对本工程中最短索A1、最长索A11进行索导管安装角度修正计算；同时，为了得到本文计算公式的适用范围，假设一对150 m长的拉索A12，其余各项参数与A11相同。

第2节中介绍了4种常规索导管安装角度修正方法，有限元电算方法在这里不作比较。为了在表达上清晰、方便，将整体计算法、悬链线法、视拉索截面弯矩为0的局部分析法、本文所述方法依次命名为方法一、二、三、四，计算结果对比见表2。

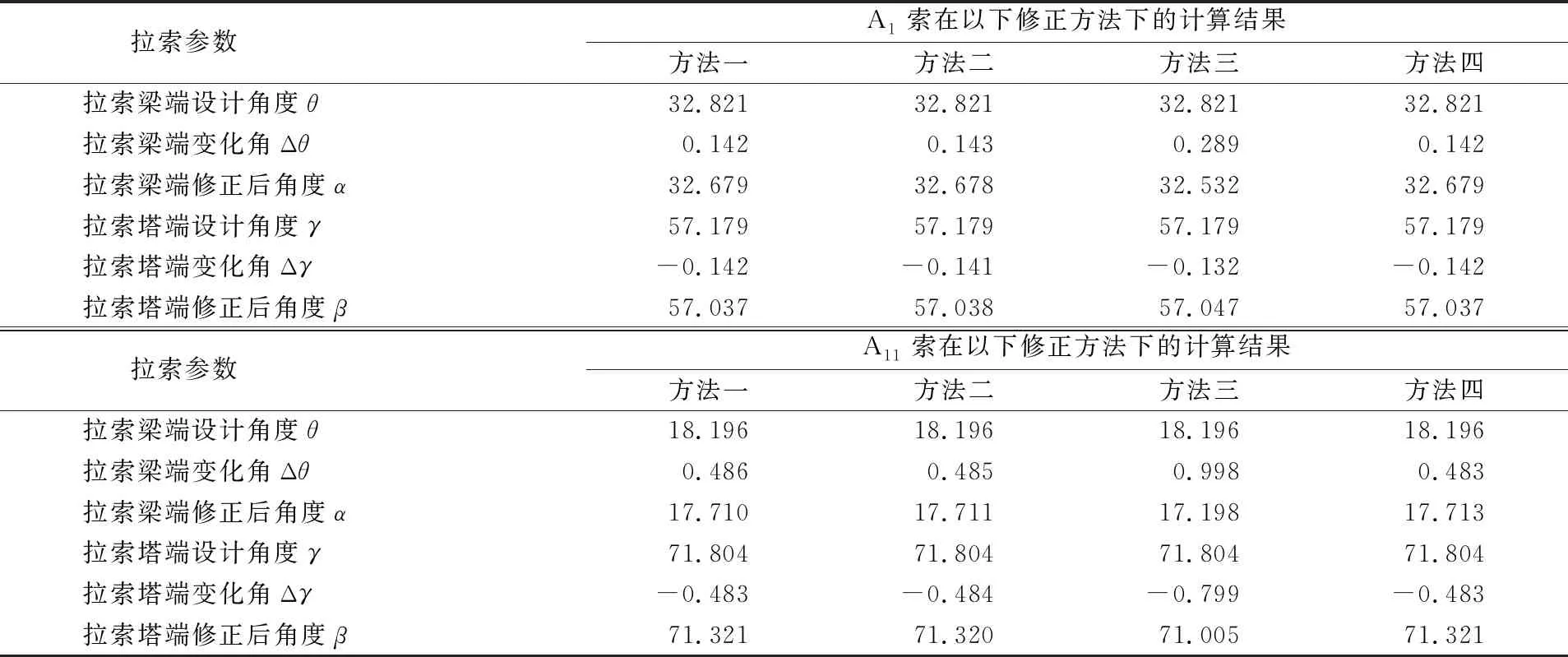
表2 各修正方法计算结果对比 (°)

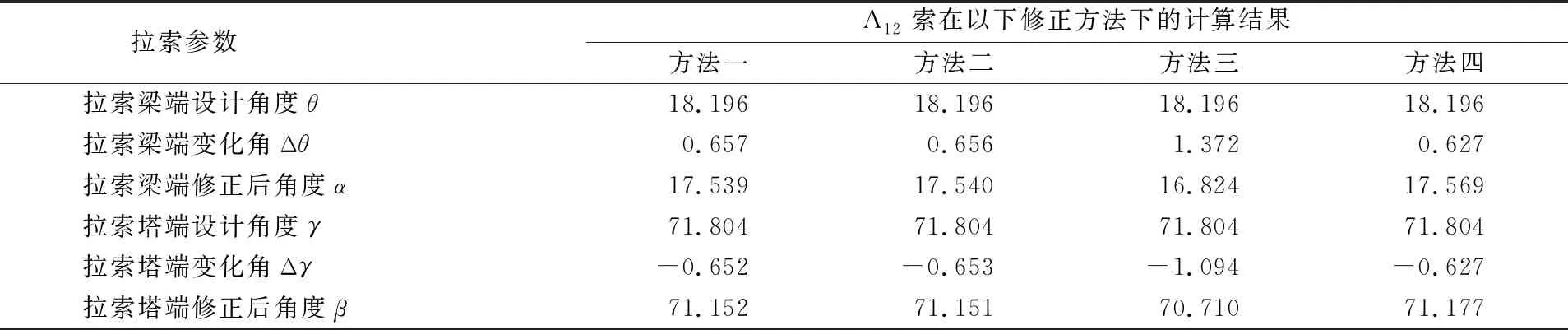
续表2

分析表2可知。

1) 本文所述修正方法计算结果与整体分析、悬链线法计算结果符合度极高。这说明考虑拉索抗弯刚度对短索索导管安装角度修正的方法符合工程要求，并具有较高的准确性。

2) 从假设的A12号拉索计算结果可知，本文公式在拉索长度达到150 m时适用性仍较高。

3) 方法三计算的修正角度误差随索长的增加而增加，显然该方法不适用于常规斜拉桥高塔长柔索的角度修正计算。

5 结论

斜拉索预埋导管的安装精度主要由测量放样和定位施工两部分决定，在施工之前根据现场施工情况对预埋导管安装角度做理论上的修正是精确放样的重要前提。本文针对短斜拉索，考虑拉索抗弯刚度的影响，推导得到了考虑斜拉索自身抗弯刚度时索导管安装角度的修正计算公式，并将该公式应用于实际工程中。主要结论如下。

1) 实际应用结果及与其他方法计算结果表明，本文所推导的计算公式能较好地满足工程需求，并且具有较高的准确性。

2) 从塔端、梁端变化角计算公式可以看出，斜拉索两端切线倾角与斜拉索索力、弹性模量、截面特性、自重集度、索长等众多因素有关。若想得到更加精确的解，必须对这些物理量进行合理的修正。

3) 本文所述修正方法计算得到塔端与梁端拉索倾角变化值相同，符合杆件在对称荷载下变形规律，进一步验证了公式推导的正确性。

4) 计算结果表明，当索长达到150 m时，本文计算公式仍然适用，但随着索长不断增加，斜拉索自身抗弯刚度将快速降低，此时斜拉索可视为理想柔性体，只承受拉力，这时本文推导公式将不再适用，应根据拉索实际情况，选择合理的修正方法。

5) 几种方法计算结果对比表明。视拉索截面弯矩为0的局部分析法与本文所述方法适用于矮塔斜拉桥刚度较大的粗短斜拉索，整体计算法、悬链线法、有限元计算法则对于矮塔斜拉桥与常规斜拉桥都适用。