基于ALGOR的桥梁锚固块应力分析及配筋设计研究
张世冀
(贵州省交通规划勘察设计院股份有限公司 贵阳 550001)
在公路和城市道路的桥梁中,多跨连续梁、连续刚构中支点附近弯矩较大,往往以锚固块作为锚固方式增加负弯矩束以抵消此处的拉应力,锚固块是预应力混凝土桥梁的关键构造之一,直接关系到预应力效果好坏。由于关于锚固块受力分析和配筋的资料较少,JTG 3362-2018《公路钢筋混凝土及预应力混凝土桥涵设计规范》(下称《18版规范》)中对锚固块锚固D区的应力分析也缺少完整的指导,给出的5个受拉部位的拉力值也不利于直接指导设计[1],导致部分工程设计人员在锚固块分析方面认识不足,概念模糊,加之施工质量控制不到位,锚固块开裂现象时有发生,严重影响预应力的有效性。而预应力有效值的降低,会造成桥梁下挠的进一步扩大,加大了预应力桥梁长期挠度值,对桥梁长期使用的安全性和耐久性造成重大影响。
1 工程概况及分析对象
分析对象为某城市桥梁37.5 m+65 m+37.5 m预应力混凝土变高连续箱梁的支点负弯矩束锚固区,根据圣维南原理,取锚固块长5 m,锚固块前后各2.5 m长的半箱梁段进行分析,由于尺寸取值较大,可忽略局部边界对锚固块本身的影响。
该箱梁采用C50混凝土,单箱单室断面,顶板宽13 m,底板宽7 m,两侧悬臂翼缘板宽3 m;箱梁根部腹板外侧梁高H根=3.5 m,跨中及边跨现浇段腹板外侧梁高H中=1.8 m,箱梁梁高按1.8次抛物线变化,锚固块的具体尺寸及与箱梁的预应力对应关系见图1。
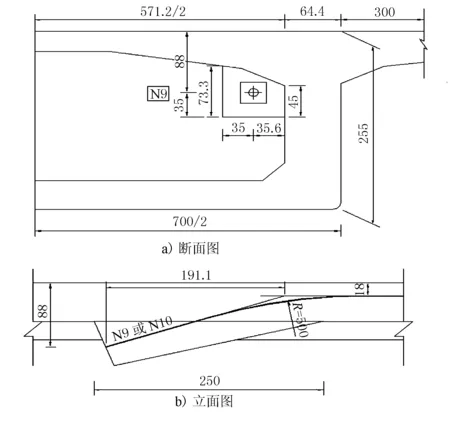
图1 锚固块结构示意(尺寸单位:cm)
2 规范锚固区计算方法
后张预应力三角齿块锚固区存在集中锚固力的作用、几何形体上的突变,以及预应力钢束弯起引起的径向力作用,是一个十分复杂的典型应力扰动区。
三角齿块锚固区内有5个受拉部位的拉力设计值,规范中给出相应的计算方法[1]。
1) 锚下劈裂力设计值
式中:Pd预应力锚固力设计值,取1.2倍张拉控制力,kN;a为锚垫板宽度,m;d为锚固力中心至齿板上边缘的垂直距离,m。
2) 齿块端面拉力设计值
Ts,d=0.04Pd
3) 锚后牵拉设计值
Ttb,d=0.2Pd
4) 边缘局部弯起引起的拉力设计值
式中:d为锚固力作用点至壁板中心距离,m;e为锚固力作用点至壁板中心距离,m。
5) 边缘局部弯起引起的拉力设计值
TR,d=Pdα
式中:α为预应力钢筋转向前后的切线夹角,rad。
JTG D62-2004《公路钢筋混凝土及预应力混凝土桥涵设计规范》没有对齿板局部受力做出说明,《18版规范》对锚固区5个主要力的数值给出了计算方法,但对根据计算出的力值如何设计配筋没有提出相应条款,规范中的公式使用起来仍然不够方便。
齿块局部尺寸较小,只能通过实体计算的方法计算局部应力的大小。规范提出的5个主要应力的思路是正确的,所以沿用规范里提出的思路,按照18版规范的方法,采用有限元计算仍然是可行的。
3 有限元法及有限元模型建立
锚固块尺寸较小,必须建立三维有限元实体模型进行局部应力分析,由于压浆后应力会随受压面积的增加而降低,所以该计算模型只考虑张拉时锚固区的应力状态,不注重预应力传递和锚垫板的应力扩散,将预应力管道从实体模型中扣除[2],施加的预应力荷载为张拉力经锚垫板扩散后的面力。
模型前后端面边界为固定约束,约束3个方向的自由度。取横向1/2作为研究对象,在对称面上施加对称约束,约束1个方向自由度。划分网格时,主要以六面体单元为主控制单元划分,最小单元尺寸控制在0.1 m,在锚固块与箱梁的相交位置,对网格进行细化,以提高锚固块作为最终研究对象的计算精度[3-4]。
通用的有限元分析CAE软件ALGOR块体分析方面功能强大,操作简单,特别在网格划分方面有较大的优势。计算采用ALGOR建立有限元模型划分网格后的实体模型见图2。

图2 结构三维离散有限元模型
4 锚固区应力分析
研究的锚固块长度5 m,钢束弯折角度为14.9°,锚固端面钢束距离外侧边距35 cm,距离内侧距离为30 cm,预应力束距离径向锚固块边缘37 cm。
齿块受力受到梁体整体受力的影响较小,主要受到自身重力及锚固力的作用。锚固块钢束为Φs15.2-19,张拉控制应力为1 395 MPa,考虑1.2倍的安全储备系数[5],经锚垫板应力扩散后,施加在锚固块锚垫板下的预应力为80.86 MPa。
锚固块为梁体的外部构件,梁体本身的受力影响较小,主要为预应力束的张拉控制应力。通过对锚固块进行实体单元应力分析,得到锚固块局部主应力图见图3。
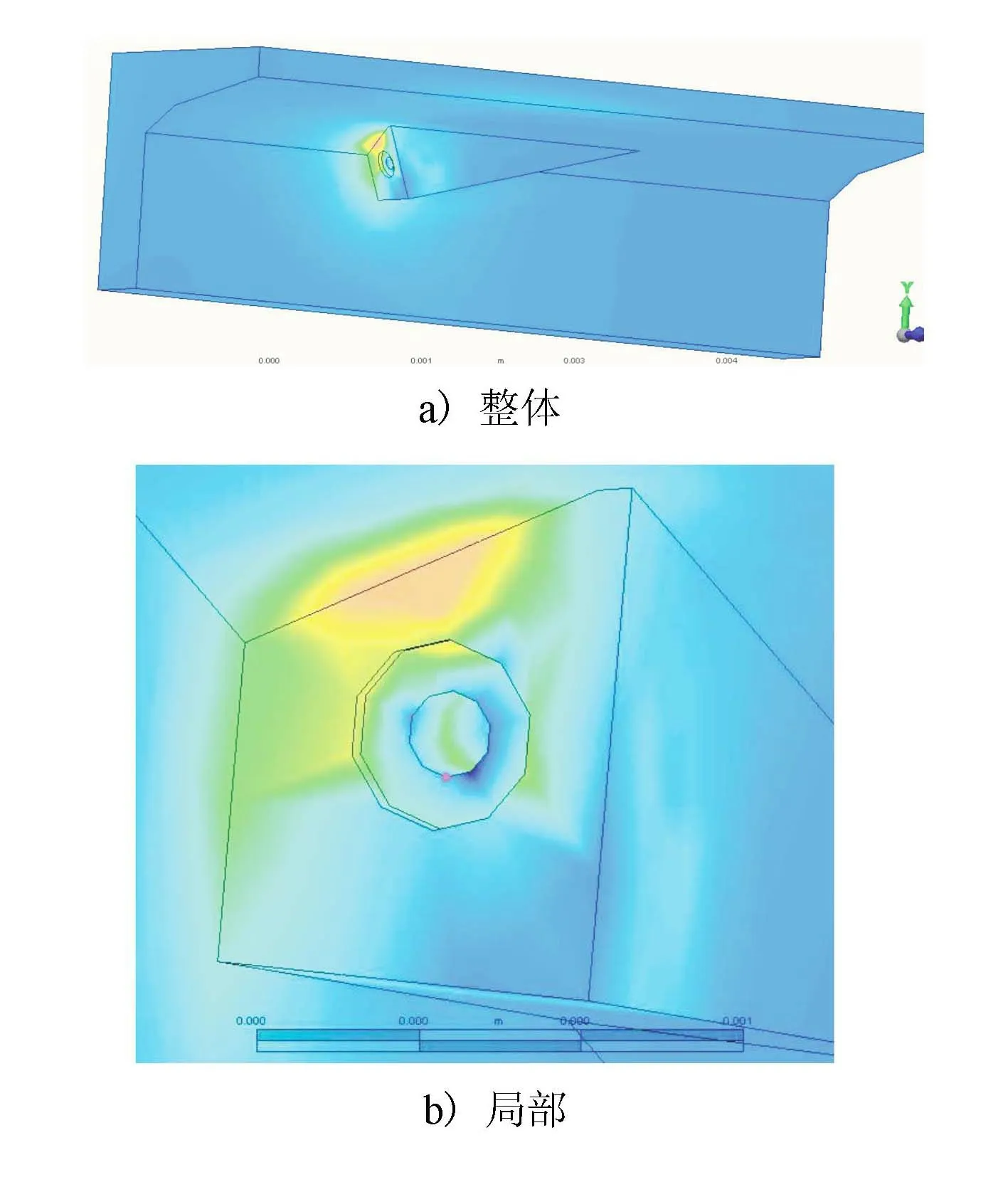
图3 锚固应力云图
由图3可知,在锚固块预应力束锚固区范围,除了《18版规范》中所论述的局部承压外,还存在其他4处应力集中区域[6]:①锚块下横向拉应力分布,称为“锚下劈裂应力”;②锚块端面根部凹角区的拉应力集中,称为“悬臂根拉应力”; ③锚后拉应力集中现象,称为“锚后牵拉效应”;④箱梁底板下缘拉应力区,称为“局部弯曲效应”;⑤预应力钢束转向区域拉应力集中,称为“径向力效应”。采用有限元计算方法,计算结构显示与《18版规范》中5个主要力的思路基本一致,基本上囊括了锚固块开裂的主要原因。
5 结果分析
根据设计经验,锚固块预应力钢束的弯折角度通常取 12°~15°,由于钢束弯折角度较大,锚固块长度较长,锚固块区域预应力水平分量减小,从而削弱了锚后牵拉效应,并随着预应力距离顶板距离的增加,刚度变大,局部弯曲效应也随之减小,同时预应力的垂直分量增加了锚固块与箱梁底板、腹板交接悬臂根部的拉应力;由于锚固端面钢束距离外侧边距和预应力束距离径向锚固块边缘距离较大,钢束外侧混凝土厚度较大,抵抗径向力效应的能力提高,径向力引起的锚固区拉应力也有效的减小。
下面通过在锚固块端面建立闭合路径,通过主应力的大小分布来研究锚固块锚下劈裂力和悬臂根部拉应力的情况。端面路径1的节点号依次为25→713→726→491→492→752→778→31→845→813→32→925→900→507→515→508→513→509→440→34→489→505→550→506→57→65→24→77→332;锚下内边缘路径2的节点号依次为49→991→50→976→2→961→936→35→36→921→90→6→37→955→38→3→47→930→48。
绘制路径1主应力分布见图4。
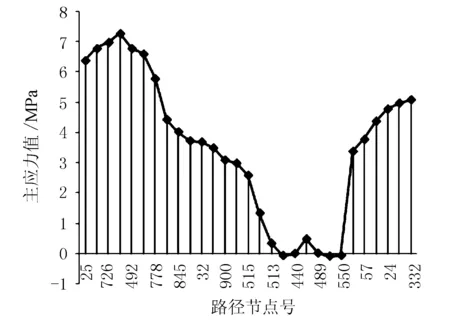
图4 路径1主应力分布
由图4可知,由于预应力束的空间效应,在锚固块与混凝土箱梁的2个接触面上锚块悬臂根部拉应力较大,其中锚固块与顶板的接触面较明显,与腹板的接触面次之,在剩下2个自由边上应力明显变小,应力集中现象更是加剧了这种应力的分布。根据计算结果来看,顶板接触面上应力集中点应力值最大可达到7.68 MPa,而腹板接触面最大应力也可以达到5.77 MPa。锚垫板对预应力的扩散作用使得锚下应力得到了极大的改善,但由于锚固块局部尺寸的作用,局部应力还是得到了加强。
绘制路径2主应力分布见图5。
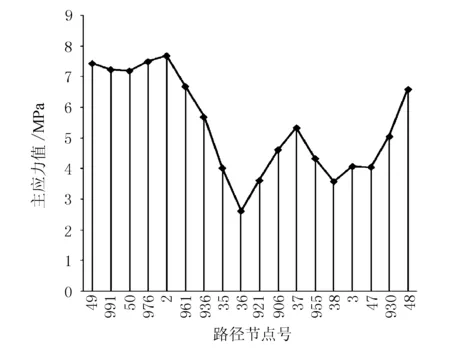
图5 路径2主应力分布
由图5可知,在锚垫板以下应力主要表现为锚下劈裂应力,同时在2个与箱梁的接触面上,劈裂应力与悬臂根部拉应力产生叠加效应,使合成应力变大,应力分布也更加复杂,另外2个自由边上则是表现为较为简单的锚下劈裂应力。根据计算结果,锚下劈裂应力为2.7~5.4 MPa,悬臂根部拉应力的叠加可使合成应力达到7.68 MPa。
根据以上5种应力的大小和分布情况,采用的锚固块配筋形式见图6。
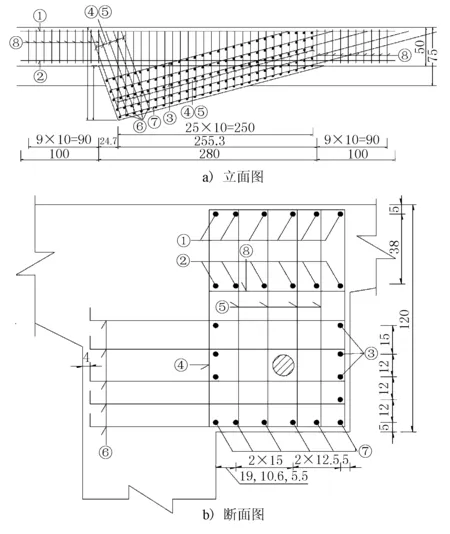
图6 锚固块配筋(尺寸单位:cm)
由图6可见,在采用较长的锚固块长度、较大的钢束弯折角度和较厚边距的情况下,应着重加强锚固块与箱梁接触面上的锚固钢筋(4,5,6号钢筋)和锚下(3,4,6号钢筋)的防劈裂分布钢筋网,以克服悬臂根部拉应力和锚下劈裂应力。
在锚固块的应力水平和图6配筋水平下,37.5 m+65 m+37.5 m预应力混凝土变高连续箱梁锚固块裂缝宽度为0.11 mm,总体锚固块应力水平较低,满足规范裂缝宽度验算要求[7]。
6 结论
通过对某箱梁锚固块进行三维有限元实体分析,并研究锚固块的结构尺寸特点及受力大小和分布,得出以下结论。
1) 预应力钢筋混凝土锚固区主要的应力有5种:锚下劈裂力、悬臂根拉应力、锚后牵拉效应、局部弯曲效应和径向力效应。这5种应力受到应力集中、空洞消弱、耦合叠加等因素影响,使得最终的应力分布更加复杂,在设计中必须引起足够的重视,直接关系到预应力的质量。即使采用有限元实体计算的方法,延续这5种力的思路仍然是可取的。
2) 由于锚固块关系到预应力的有效性,建议设计中应该考虑较大的安全富余度。从设计便利方面考虑,采用合理的锚固块结构尺寸和预应力弯折角度可以有效降低锚后牵拉效应、局部弯曲效应和径向力效应,若同时采用有效的钢筋布置加强锚下和牛腿抵抗锚下劈裂应力和悬臂根部拉应力,这种方法在设计中非常实用且安全性较高。
3) 锚下劈裂应力和悬臂根部拉应力无法避免,应力集中和叠加现象也使得这2种应力变大和更加复杂,因此,建议在设计中加强对锚固块与箱梁接触面上的锚固钢筋和锚下的防劈裂分布钢筋网的设计,尽量增加这2种钢筋的配筋率。现实中箱梁接触面和锚下也是发生问题常见的地方。
4) 出于锚固块应力状态较高和受力复杂状况的考虑,锚固块设计配筋率往往较高,这有利于提高锚固块的抗裂性能,但对混凝土施工造成一定困难,后期应加强施工质量管理,务必保证锚固块混凝土的密实。

