基于FRFT的多重分形海面小目标检测

邵夫驰，行鸿彦

(1.南京信息工程大学气象灾害预防预警与评估协同创新中心，江苏 南京 210044;2.南京信息工程大学江苏省气象探测与信息处理重点实验室，江苏 南京 210044)

0 引言

海杂波是海洋表面对雷达信号的后向反射回波，受到海上复杂海情的影响，对待检测海面上小目标有着巨大的阻碍。20世纪80年代，分形理论的提出给海杂波背景下的目标检测创造了契机[1]，分形是事物局部和整体有相似性的体系，现在利用分形理论研究海杂波依旧是雷达信号处理领域的热点。

对海杂波进行统计建模[2]往往建立在海平面平稳的条件下，但是海杂波具有强烈的非平稳性，海杂波复杂的物理特性无法靠单一的统计特性进行表示，当海情变换且信杂比较低时，基于统计模型的检测效果基本失效。1990年，Haykin等[3]证实海杂波并非属于随机过程而是混沌系统。随后相关研究者[4-5]在此基础上提出了混沌相空间重构法、支持向量机(SVM)、径向基函数(RBF)等与神经网络相结合的方法来检测小目标，但是训练时间长，结果泛化性差，不能满足实际需求。Lo等[6]提出单尺度分形维数分析海杂波，利用存在目标区域的海杂波分形维数与周边无目标区域的海杂波分形维数的差异进行目标检测。文献[7]提出了在时域中基于单尺度分形特性，利用Hurst指数的分形差量进行小目标检测，较好在时域上实现对目标的检测。文献[8—11]提出了在FRFT域上采用变阶数的多重分形去势波动分析方法检测湮没在复杂海情中的小目标。分数阶Fourier变换(FRFT)[12-13]是经典Fourier变换(FT)的广义推广，能够对运动的目标进行能量聚集，提高信号的SCR，海杂波信号属于SCR较低的信号，为将FRFT应用于海杂波数据的处理提供了依据。针对海杂波背景下复杂海情对小目标检测的影响，上述方法未考虑海杂波信杂比低的特性，本文提出了基于FRFT的多重分形海面小目标检测方法。

1 基本理论

1.1 分数布朗运动建模

假设某一随机连续信号是自相似信号，自相似信号的定义式为：

(1)

1968年，Mandebrot等[14]从布朗运动中推广得到分数布朗运动，定义式为：

(2)

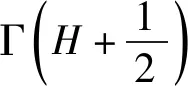
(3)

式(3)中，H为Hurst指数，表征数据间的相似性关系，自相似分数维数D与H存在线性关系：

H=2-D

(4)

由(4)式可知，Hurst指数与分数维D成反比，H和D选用一个表征分形特性即可。

分数布朗运动本身不是平稳过程，具有自相似性，但是它的增量是满足高斯分布的平稳随机过程，其分布满足N(0,δ2)，其中δ是非零值。所以有：

BH(t+1)-BH(t)～N(0,δ2)

(5)

Var(BH(t+τ)-BH(t))=δ2τ2H

(6)

式中，τ为时间延迟，Var为方差函数,分数布朗运动选用H作为表征数据分形特性的参数。文献[15]采用分数布朗运动对海杂波进行建模，与Hurst指数相结合，实现了在同一种海情下小目标的检测,证明利用分数布朗运动对海杂波进行建模的可行性。

1.2 海杂波FRFT的分形理论

1.2.1自相似过程FRFT的自相似特性分析

分数阶Fourier变换(FRFT)由传统Fourier变换的广义推广[16]得到，时域函数x(t)的p阶FRFT是一个线性积分运算，定义式：

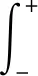
(7)

式(7)中，Kp(t,u)是FRFT中的核函数。

(8)

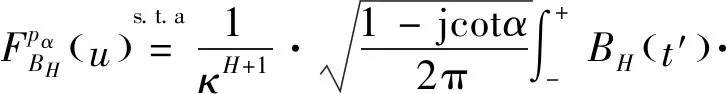
(9)

(10)

对式(10)进行取模得：

(11)

由式(11)可知，在同一变换阶数下，BH(t)的FRFT谱的幅度值不是尺度不变的，而是随着尺度参数κ改变，变换阶数pβ也随着改变。因此，当尺度发生改变的时候，变换阶数也需要随着改变，才能起到放大分形差异的效果。尺度参数和变换阶数同时改变，给数据的处理带了较大的不确定性，描述FRFT谱的分形特性采用单一分形参数可能会带来误差，使多重分形分析成为可能。

1.2.2计算多重分形参数

2002年，Kantelhardt等[17]提出了多重分形去势波动法(MF-DFA)，可以消去局部趋势对时间序列的影响，是当前研究非平稳有限长时间序列的主要方法，能够研究序列在不同标度下的分形特性。采用MF-DFA对Hurst指数进行估计。MF-DFA计算分形参数，主要分为如下5步：

1) 对时间序列是否满足随机游走序列特性进行判断，如果时间序列满足，则跳过本步骤；不满足，则构造去均值求和序列：

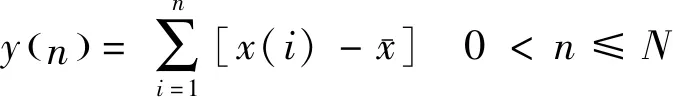
(12)

3) 对子序列按式(13)、式(14)求均方差，即为子序列的局部震荡，yi,fit(n)为子序列最小二乘拟合多项式。当时间序列长度较长时，则只要计算式(13)：

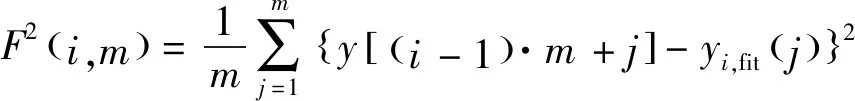
(13)

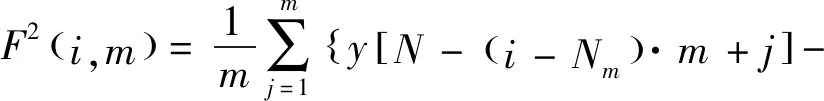
(14)

4) 计算q阶波动函数

(15)

Fq(m)是关于分形阶数q和子序列长度m的函数，q为非零实数；

5) 根据关系式Fq(m)～mH(q)，利用最小二乘法，对关系式的双对数曲线进行线性拟合，斜率即为分形参数，所以可以通过改变分形阶数q，得到不同尺度下的分形参数H(q):

(16)

如果H(q)与q不相关，则表示Fq(m)与q也不相关，代表时间序列的局部结构满足一致性，时间序列具有单分形特性；如果H(q)与q有关，代表时间序列的局部结构不满足一致性，是非均匀的、不一致的，时间序列具有多重分形特性。当q=2时，H(q)是Hurst指数。

2 基于海杂波FRFT的多重分形特性小目标检测

本文选用麦克马斯特大学IPIX雷达的实测海杂波数据，实测数据包含392组数据，每组数据长度为131 072，每组数据代表某种海情下雷达工作在某一个极化方式下的某个距离门的数据，一共有2个极化方式，14种海情和14个距离门，并且标明了纯海杂波和主、次目标所在的距离门。IPIX雷达发射频率为9.39 GHz，脉冲重复频率为1 kHz。海面上需要检测的小目标，是一个直径为1 m的塑料小球，外围包裹着金属网。

2.1 海杂波数据的FRFT谱

图1是HH极化和VV极化#17海情下，第九距离门海杂波时间序列在各阶变换阶数的FRFT幅度谱图。如图所示，不同的变换阶数,幅值起伏较大，只根据幅值无法判断纯海杂波和小目标，原因是小目标和海情自身均有加速度和速度，FRFT难以针对性的对小目标信号进行补偿。

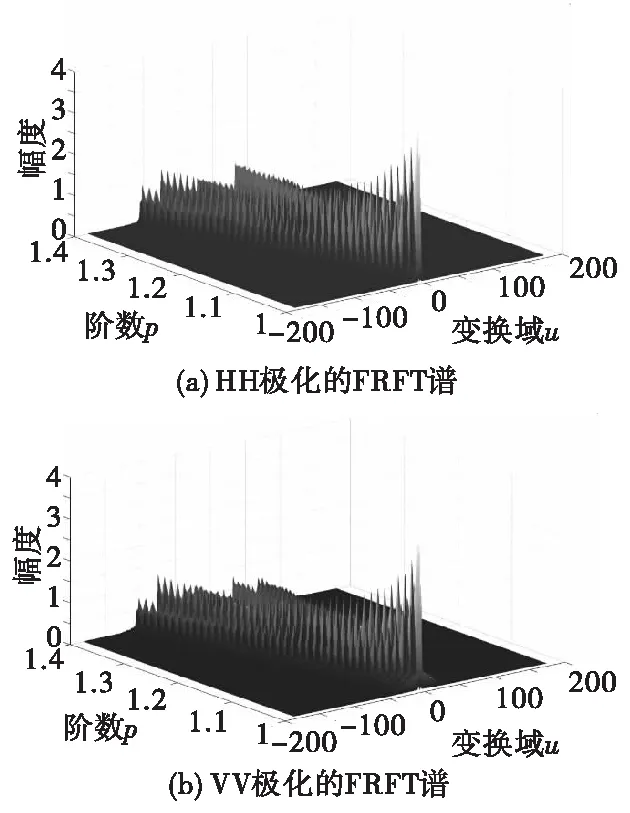
图1 不同极化的FRFT幅度谱Fig.1 FRFT Amplitude spectrum with different polarization

文献[8]中假设FRFT域的海杂波增量是遍历的，实验结果增量分布大致符合高斯分布，将增量分成几个相互不重叠的子集，发现方差几乎不随时间改变，与FBM模型的性质相同，可以用FBM对海杂波FRFT域进行建模。

2.2 选取最佳FRFT阶数的理论

分形维数是表征物体不规则性和复杂性的参数，本文所用数据观测的小目标为人造包裹金属网的塑料小球，表面光滑，海面则比较“粗糙”。假设在观测时长T内，雷达回波的模型[18]表示为：

x(t)=s(t)+w(t)=Aejπ(2f0t+μ0t2)+w(t)

(17)

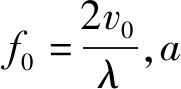
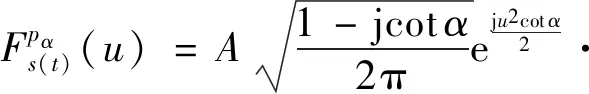
(18)

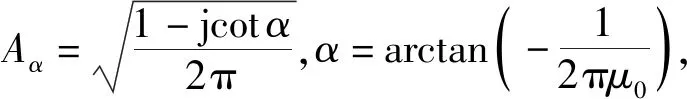
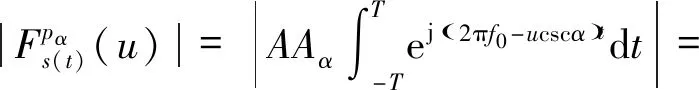
(19)

由式(19)可知，当|Sa(α)|求最大值时，即最佳旋转角度与目标速度状态相匹配，得：

(20)

此时回波能量最佳聚集，为一冲击函数，目标回波与纯海杂波的分形特征差异最大。

3 基于FRFT域的多重分形特性小目标检测验证

MF-DFA对海杂波FRFT域的不同海情与不同极化的数据进行处理，基于海杂波自身的多重分形特征进行分析。图2是#17海情在雷达系统HH极化下第一距离门实测数据的最佳变化阶数的FRFT值的多尺度Fm(q)-m的双对数图。图中的纯虚经的尺度为正值，带星虚线的尺度为负值，图中曲线自上而下对应的尺度q=30,25，…,1,-1,-5,…，-30。

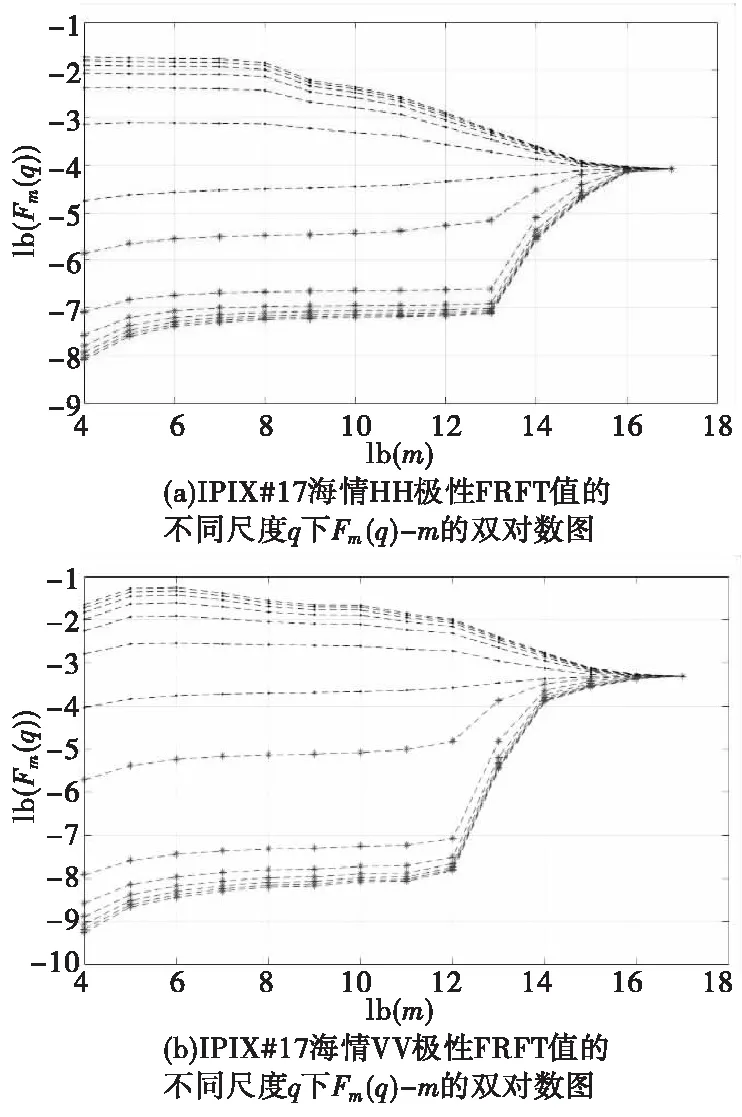
图2 FRFT值的Fm(q)-m的双对数图 Fig.2 The double logarithmic diagram of Fm(q)-m of FRFT value

观察图2，在高尺度下，曲线都表现出一定的聚集性，说明在高尺度下波动曲线相似。HH极化，区间4～15表现出一定的线性关系；VV极化，区间4～12表现出线性关系，可认为是多重分形区间。

由图3可知在高尺度情况下时间序列同样表现出一定的聚集特性，HH极化，区间4～14表现出一定的线性关系；VV极化，区间5～12表现出较好的线性关系，最佳变换阶数的FRFT域与时间域相比，线性区间得到了拓展，HH极化线性区间提高了10%，VV极化线性区间提高了14.29%，为检测小目标的准确性提供了帮助。

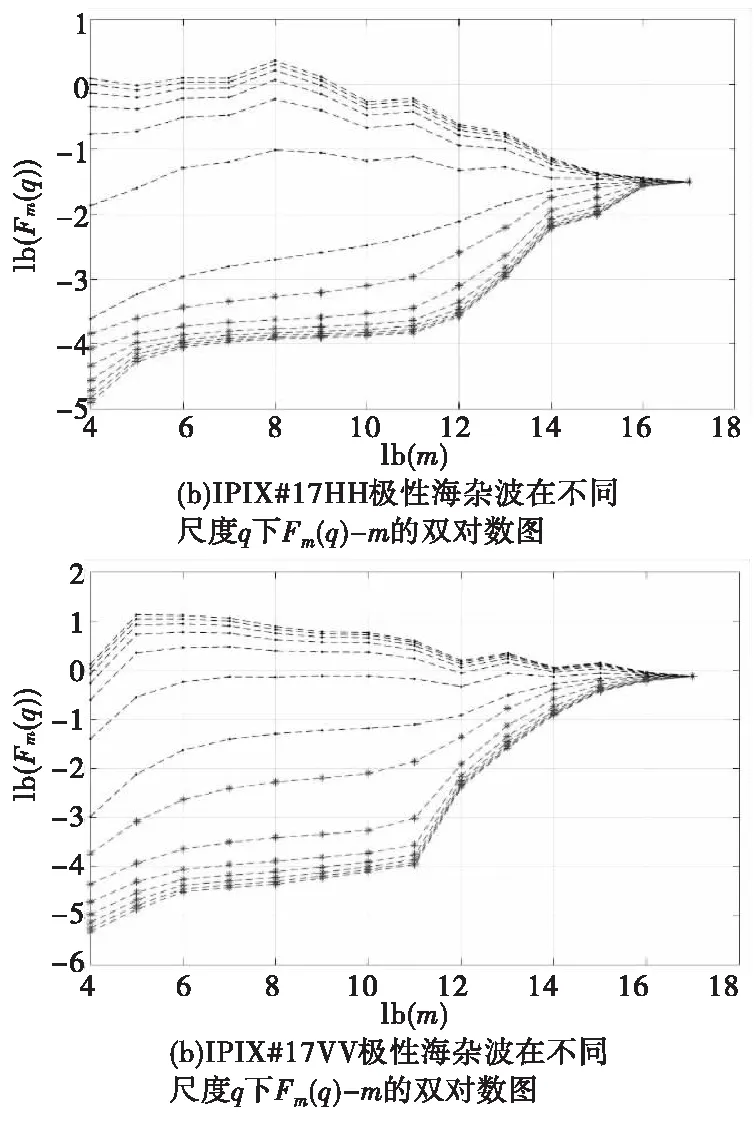
图3 时间序列的Fm(q)-m的双对数图Fig.3 The double logarithmic diagram of Fm(q)-m of time series

选取不同极化、不同海情的实测数据，对不同情况下海杂波多重分形参数H(q)进行分析。如图4在HH极化和VV极化下分别选择了#31和#311海情的最佳阶数的FRFT域数据，纯海杂波选择它们共同的第二距离门数据，小目标信号选择各自海情主目标所在的距离门单元。如图4所知，不同极化和不同海清的海杂波数据均满足多重分形特性，在高尺度时有着稳定的多重分形参数。可采用高尺度多重分形参数H(q)的差值，对小目标进行判定。在负高尺度HH极化的多重分形参数H(q)的差值略高于VV极化，在正高尺度HH极化的多重分形参数H(q)的差值略低于VV极化。

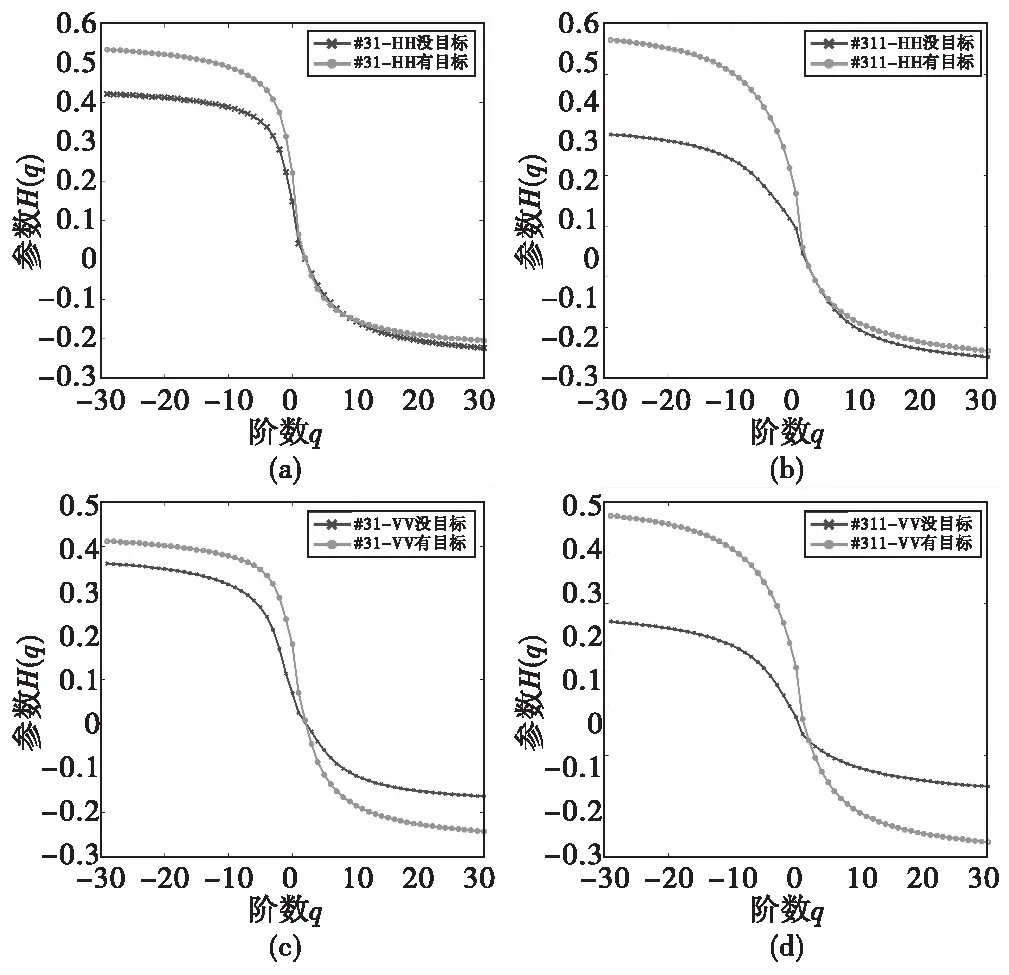
图4 高尺度多重分形参数H(q)的变换情况Fig.4 Transform of high scale multi-fractal parameter H(q)

同时分析同种海情下不同距离门的最佳阶数FRFT域的多重分形参数，选用HH极化和VV极化的#17海情，如图5，发现在负高尺度时，不同距离门的纯海杂波多重分形参数在HH极化时比较集中，在正高尺度时，不同距离门的纯海杂波多重分形参数在VV极化时比较集中，说明同一种海情下，纯海杂波的高尺度多重分形特性基本一致。

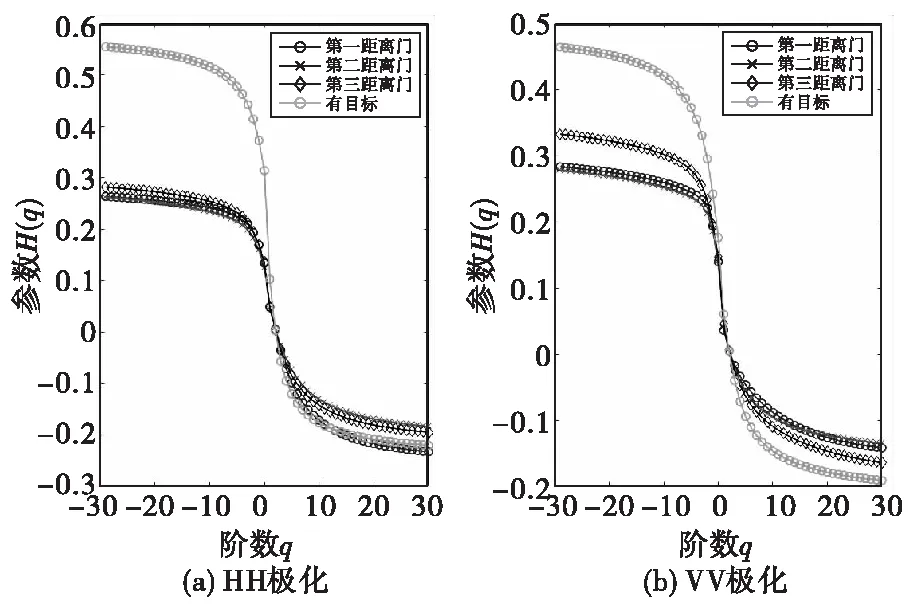
图5 高尺度多重分形参数H(q)的变换情况Fig.5 Transform of high scale multi-fractal Pparameter H(q)

由图4和图5得到，可利用有目标的高尺度分形参数H(q)与无目标的高尺度分形参数检测小目标。在雷达工作在HH极化时，选择负高尺度对小目标进行检测；在雷达工作在VV极化时，可选择正高尺度对小目标进行检测。

图6所示为各距离门在高尺度下分形参数H(q)的值。当距离门有小目标存在，会发生跳变，实现了同种海情下对小目标检测的需求。但是不同的海情下，很难统一一个门限值，难以准确的分辨有无小目标，可对各个海情高尺度分形参数分别进行归一化，结果如图7所示。

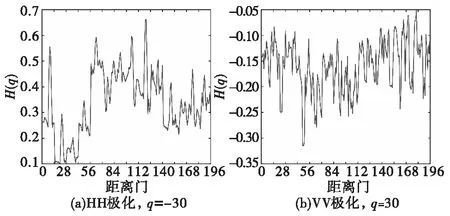
图6 高尺度各距离门H(q)值Fig.6 H(q) Values of high-scale distance gates

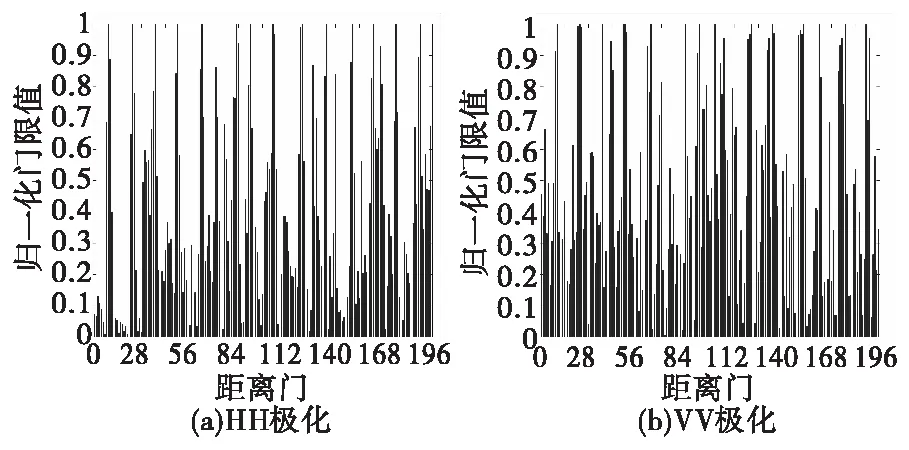
图7 高尺度各距离门归一化后H(q)值Fig.7 Normalized H(q) values of high-scale distance gates

如图7所示，在主目标检测时，在HH极化，可设置归一化后的门限值为0.65，当达到0.65，判定为有目标，正确检测率为84.69%，主目标检测正确率为92.86%，#30海情主目标未检测到，其他13种海情均能检测出主目标；在VV极化，可设置归一化后的门限值为0.9，当达到0.9，判定为有目标，正确检测率为85.20%，主目标检测正确率为78.57%。实验发现，HH极化的检测效果高于VV极化，同时发现次要目标所在距离门与主目标距离门相聚越远，信杂比越小，检测到目标的难度越大。本方法易于实现，计算量小，能够快速检测目标信号。

4 结论

本文提出了基于FRFT的高阶多重分形海面小目标参数检测方法。该方法选用分数布朗运动(FBM)建模，将海杂波数据代入FRFT变换，发现不再具有严格的自相识性，除了FRFT变换阶数，还与尺度系数有关，再利用多重分形去势波动法确定多重分形参数H(q),研究海杂波实测数据在不同组合下的多重分形参数。海杂波序列在FRFT域相比时域，延拓了多重分形区间，HH极化提高了10%，VV极化提高了14.29%。雷达系统工作在HH极化下，负高尺度检测效果优于正高尺度；雷达系统工作在VV极化下，负高尺度检测效果略差于正高尺度。并且同一海情下，不同距离门纯海杂波的多重分形特性基本一致。对高尺度分形参数进行归一化，设置门限值，HH极化设立门限值为0.65,VV极化设立的门限值为0.9，检测正确率为84.69%和85.20%，主目标检测正确率为92.86%和78.57%。检测实验为海杂波在FRFT域上检测小目标提供了依据，比传统时域分形检测方法和单一分形参数检测方法具有更好的检测效果。