共享频谱雷达恒模发射波形设计方法

张令浩，张剑云，周青松

(国防科技大学电子对抗学院，安徽 合肥 230037)

0 引言

射频资源是宝贵的自然资源，近年来，众多服务包括雷达、通信围绕这一资源的争夺愈发激烈。特别是最近5年来，民用通信技术迅猛发展，5G通信技术也即将进入日常生活。在C波段频谱资源争夺表现地十分明显，在这一波段雷达与通信的用户地位随着通信的发展产生易位，这说明，雷达在这一波段与通信重合的射频频段必须作为“第二用户”工作。 另一方面，从雷达的角度来看，雷达发射探测信号追求高距离分辨率，而信号的带宽决定了分辨率，所以雷达系统追求占据更大带宽。实际上，不仅是通信、雷达，还有无线电定位、卫星导航、广播等领域都在迅猛发展，积极扩大自身占据的射频资源，导致射频资源紧张，交叠现象日趋严重。因此提高频谱利用效率，实现频谱资源合理共享具有深刻的现实意义。

针对当前雷达在占用频谱资源上面临一部分挑战，文献[1]作了客观分析并描述这些挑战来自于持续的频谱相互侵占，而且认为这需要增强对干扰的鲁棒性和波形多样性。文献[2—7]为实现频谱共享提供了一些波形设计技术，以使雷达信号具有某些期望的谱槽(凹槽)。与以上频谱中直接设计凹陷的思路不同，文献[8]则提出了一种利用循环方法设计具有低自相关旁瓣水平和频谱特定频率凹陷的算法。除了考虑以上这些设计波形思路，Augusto.Aubry等人在文献[9-10]中利用凸优化理论提出了一种经典方法，该算法针对时域和频域施加约束，建立凸优化问题模型，将非凸问题松弛求解，然后结合秩一分解理论[11]进行求解，并指出设计恒模波形具有更大的实际价值。文献[12]利用凸优化模型对MIMO雷达设计恒模信号，并且将发射和接收端联合考虑，进行优化，但并未对设计的波形考虑频谱兼容性。此后该团队在文献[13]提出了一种迭代算法研究了连续和有限相位字母表情况时恒模和相似约束下二次优化问题，算法复杂度较低。本文针对射频频谱环境日益拥挤、频谱利用率不高的问题，提出了利用凸优化结合迭代算法设计恒模波形的方法。

1 共享频谱恒模波形设计模型构建

本节将对恒模波形设计实现频谱共享的思想进行数学抽象，分析问题背景并建立信号、共享频谱的模型。主要考虑基于凸优化确立目标函数，添加约束条件，最终得到建立共享频谱优化波形的非凸问题模型。

假设s∈CM′×1为离散时间信号，用以表征雷达发射的探测信号波形，M′代表信号的长度。令接收信号为y，且y是M′维的快时间维列向量，从接收端分析，可以建立模型如下：

y=βs+n′

(1)

式(1)中，β代表着从已知的目标距离方向角范围内的信道传播和后向散射效应的一个复参数，n′代表着独立的信号干扰，接收机内部热噪声、干扰信号、交叠频段干扰都认为是可能的独立干扰源。总之，将n′建模为一个M维协方差矩阵，均值为零的复高斯随机向量。

众所周知，为获得较高的距离分辨率，雷达发射的探测信号需要具有良好的自相关特性。通过控制信号与参考信号的相似程度从而能够很好地控制信号的变化，这种约束方法也被称为添加相似性约束。而线性调频信号是具有良好自相关特性的雷达常用信号，通常作为相似对象。用数学表示为：‖s-s0‖2≤κ，其中κ≥0，s0为参考信号。

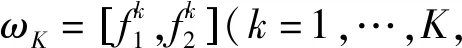
s†RIs≤EI

(2)

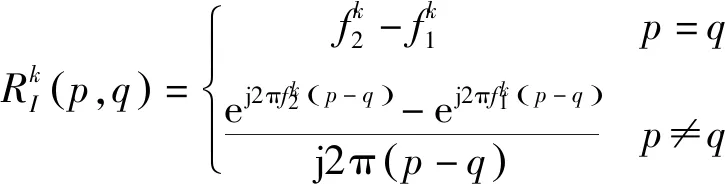
(3)

以雷达系统的检测性能为优化指标，选择输出信干噪比作为优化对象。假设信号通过线性系统，ω作为系统系数，由式(1)知，yout=βω†s+ω†n′，则输出信干噪比：

因为M1/2M-1/2=I,则有

对上式利用Schwartz不等式可以得到如下结果：

令R=M-1,希望最大化信干比，有

(4)

为实现频谱共享，文献[9]重点针对能量约束寻找优化波形做了全面的分析，本文进一步考虑贴近工程实践，改进文献[9]中的模型，寻求解决恒模波形设计的算法。

同样假设信号能量为1，信号不再为任意序列而是约束为恒模序列，考虑频谱兼容性约束及相似性约束得到：

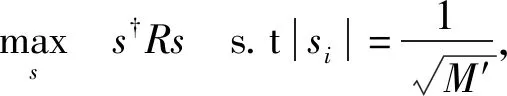
(5)

很明显模型(5)的约束条件中恒模约束是非凸集合，另一方面，除了恒模约束以外的两个约束条件会使得可行集合压缩，甚至相互矛盾导致空集。仿照Aubry等人在文献[9]对能量约束的阐述。本文对于模型(5)，仍利用凸优化方法解决。

2 非凸问题松弛结合迭代算法求解

上一小节中，利用凸优化手段建立了设计恒模发射波形实现雷达与其他服务共享频谱的数学模型，本节将讨论对建立的模型的求解问题，对非凸问题进行松弛，然后结合迭代算法寻找优化解。

首先对模型(5)进行分析，一方面讨论模型(5)的松弛求解，另一方面分析在松弛后问题的可行集区域。同时利用高斯随机化方法生成优化信号。

本文为叙述完整，下面针对模型(5)进行分析。将式(5)写成如下形式：

(6)

进一步得

(7)

(8)

式中，σ=(1-κ/2)2,S=ss†，而且‖s-s0‖2显然满足

‖s-s0‖2=[2-2Re(s†s0)]

(9)

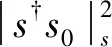
将式(6)恒模约束抛掉，将目标函数和约束条件写成迹的形式，并且只对S=ss†的主对角线元素作约束，松弛成可解的SDP问题，可以得到Q′，其中S0=s0s0†。Q′是对(6)的较大的松弛，二者并不等价，但仍然需要先给出Q′的解，然后结合迭代算法控制波形，得到效果更好的优化波形

(10)

式(10)中，S0表示S为半正定矩阵。在求解该问题之前，需要分析约束条件所构成的可行区域问题。由q1中约束条件分析，EI的取值范围应为得到式(11)的解，同时取构成可行集。其中表示问题的优化值。

(11)

进一步等效为：

(12)

如同式(6)写成式(7)，将式(11)可以写为

(13)

在这里，利用高斯随机化方法[12]寻找优化解，并令s″=s′ejarg(s′†s0)。使用该方法，选取生成的随机化次数越高，便能够越好地得到高度近似解。

由于在松弛过程中，抛掉恒模约束，使得优化解偏离最优解很多，得到信号在指定的频段能量谱密度会有所降低，但降低幅度较小，因此进一步考虑将此优化解作为相似对象，继续寻找效果更优的信号序列。

文献[13]提出一种迭代算法，可以用来在常模与相似约束下寻找频谱能量降低的信号。为保证本文结构的完整性，本文将对文献文献[13]中方法的思想进行概述，以下简称连续相位迭代算法(IA-CPC)。

首先，在上面的模型构建中，相似性约束都是利用数学表达式‖s-s0‖2≤κ，其中κ≥0，s0为参考信号。此时，考虑换另一种表述，利用m无穷范数‖s-s0‖m≤ξ，ξ≥0表示。

那么对于恒模约束和相似性约束，可以建立模型为：

(14)

进一步转化得到

(15)

式(15)中，γi=args0(i)-arccos(1-ξ2/2)，而且δ=2arccos(1-ξ2/2) 。迭代求解目标函数值，主要的思想是将信号s中M′-1个元素固定，优化剩下的一个元素，然后以此方法优化所有元素，得到一个优化信号，然后以此信号作为相似信号，重复以上步骤，当信号满足设定条件或者循环次数结束，则输出信号，具体见文献[13]。

结合上述迭代算法，便可以很好地解决设计恒模波形实现共享频谱的问题。大体思路如下：利用凸优化工具箱求解模型(10)，再用高斯随机化方法，随机生成X组零均值协方差矩阵为S的高斯随机向量，即ξi∈CM′×1,i=1,…X，并且同时满足ξi～N(0,S) ，每生成一组随机向量ξi代入目标函数表达式中得到相应的信干噪比(SINR),选取使得SINR最大的随机向量作为输出的信号s″。

然后再将s″作为相似对象, 控制相似性参数，这里取较小的参数，使优化解在较小的范围内变化，求解以下问题：

(16)

式(16)中，γi=args″(i)-arccos(1-ξ2/2) ，而且δ=2arccos(1-ξ2/2) 。

根据以上思路，本文提出的高斯随机化方法结合IA-CPC算法步骤如下：

1) 利用凸优化工具求解Q′(10)模型并得到复矩阵S′，同时计算S′的秩；

2) 若rank(S′)=1,直接对S′进行特征值分解即得到最优解，跳到步骤5)；

3) 若rank(S′)>1，以均值为零，协方差矩阵为S′随机生成X组随机向量，同时代入信噪比表达式；

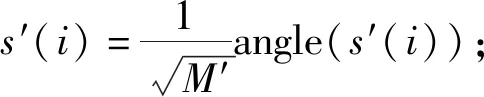
5) 取s″=s′ejarg(s′†s0)；

6) 利用连续相位迭代算法(IA-CPC)求解模型(16)；

7) 输出信号s。

3 实验仿真

本节将添加相关数值并进行仿真。需要说明的是，仿真过程中为更好地体现算法一的有效性，将先对算法一中步骤5的输出结果进行分析，然后对步骤7输出的信号作仿真。

假设相似对象为线性调频信号满足：

(17)

假设在归一化频带上，存在以下几个重叠频带，

对于干扰，假设干扰有窄带敌对干扰、白噪声以及交叠频段合法的发射器产生的干扰，各干扰源相互独立。干扰信号的协方差矩阵建模为[9]：

(18)

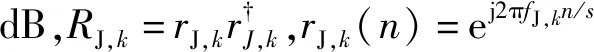
下面对模型(5)进行实验数据仿真，根据式κ≥v((Q)′EI)与式(12)、式(13)画出可行集区域(注意：在仿真图中使用E代表公式中EI)，见图1。

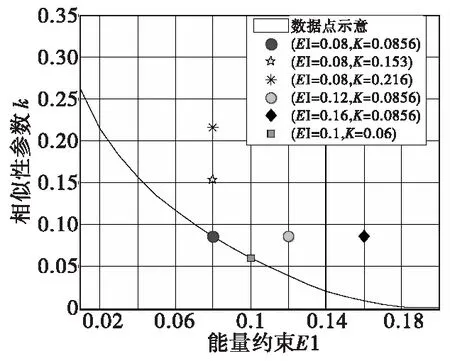
图1 干扰相似性区域Fig.1 Interference and similarity achievable region

根据图5中标注出的其中几个点的数据进行仿真(E1=0.08，K1=0.085 6)、(E2=0.08，K2=0.153)、(E3=0.08,K3=0.216)。

选择(E1=0.08，K1=0.085 6)解决问题模型(10)，利用高斯随机化方法生成信号，随机化次数选择为20 000次，并取恒模得到信号s′,仿真其自相关函数(ACF)和能量谱密度(ESD)效果如图2。

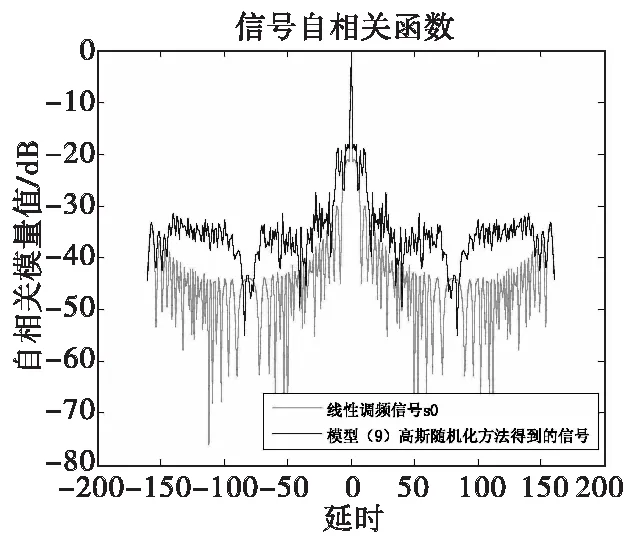
图2 高斯随机化方法自相关仿真结果Fig.2 ACF simulation results of Gauss randomization method

执行步骤5后ESD比较图如图3。

执行步骤6)、7)得到的信号自相关函数及能量谱密度结果如图4、图5。

从图2、图4中可以看出，在求解模型(10)时，利用高斯随机化方法得到的信号自相关特相较而言，高斯随机化方法得到的信号自相关特性比较好，并且图3也可以看出符合在指定的频段信号谱能量降低的恒模信号要求，说明该模型(10)在求解频谱共享恒模波形设计时是有效的。但是这样得到的信号在指定频段能量谱密度下降5～10 dB，因此考虑以此信号组为相似对象，牺牲部分的自相关特性，得到更明显的信号频谱兼容特性。所以看到图3中红色线，自相关特性变得稍差，但图5中，可以看到信号在指定频段能量谱密度降低明显。

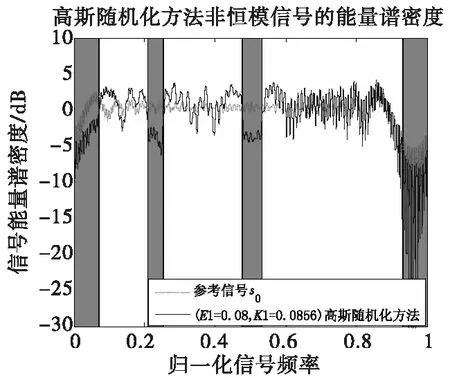
图3 能量谱密度比较效果图Fig.3 Comparison of ESD

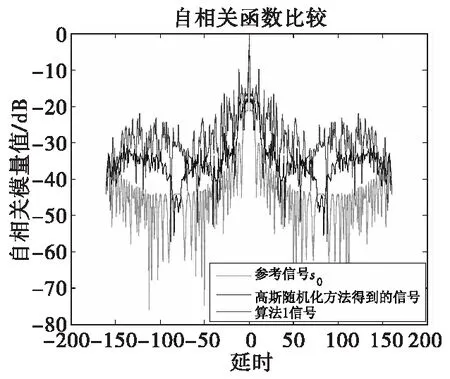
图4 自相关仿真结果Fig.4 Simulation results of ACF

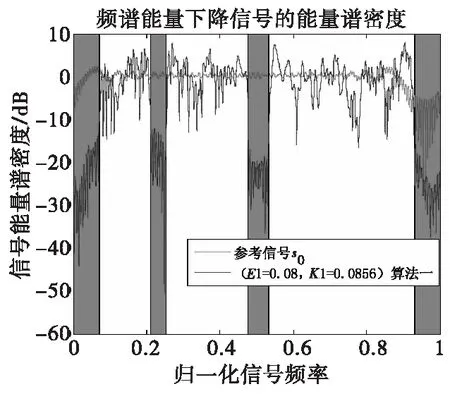
图5 能量谱密度比较效果图Fig.5 Comparison of ESD of signals

图6给出了利用本文的方法得到的信号的幅度为恒定的，利用其他数据点得到的信号幅度都是如此，后面不再重复绘制。

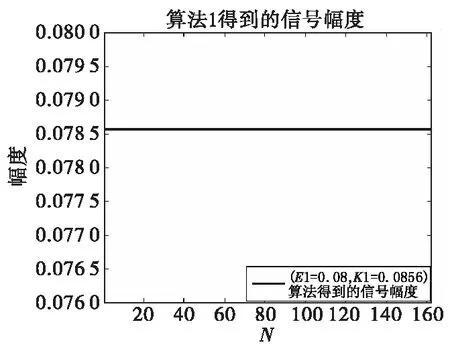
图6 信号幅度Fig.6 Amplitude of signal

下面，考虑将图1中不同的点利用本文提出的方法得到的信号进行仿真比较。图7给出了得到的信号自相关函数仿真结果，可以看到，相对于参考信号(图中绿色线)，信号的旁瓣水平虽然有所升高，但信号整体的自相关函数特性仍然得到了有效控制，换句话说，牺牲部分自相关特性换取信号的恒包络特性是有效的。

取频谱兼容性参数固定的情况下，相似性参数不同，利用图1的数据得到的信号能量谱密度结果如图8所示。

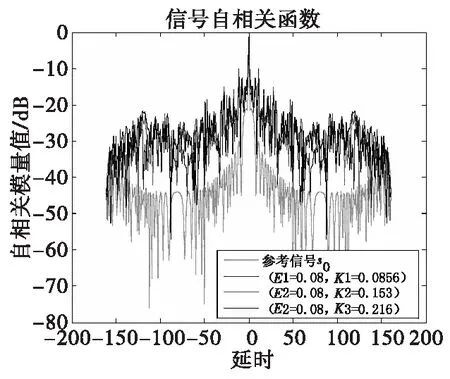
图7 信号的自相关函数仿真结果Fig.7 Simulation results of signal autocorrelation function

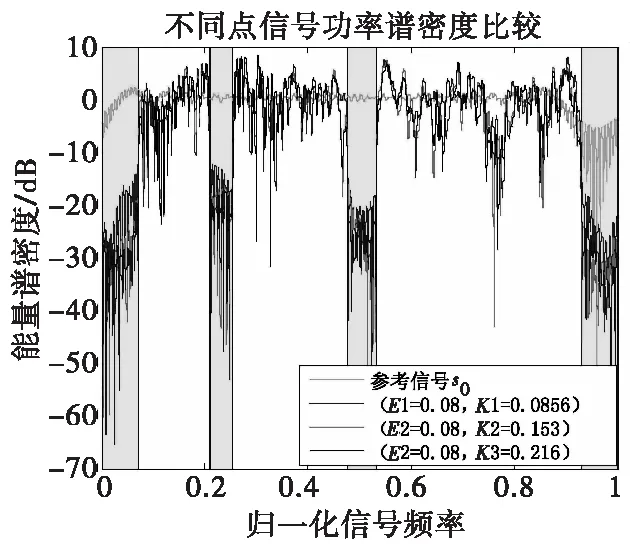
图8 能量谱密度比较效果图Fig.8 Comparison of ESD

除此之外，也对该方法得到的信号信干噪比进行仿真，给出信干噪比在E=0.08时，随着相似性参数k的变化趋势，如图9所示。

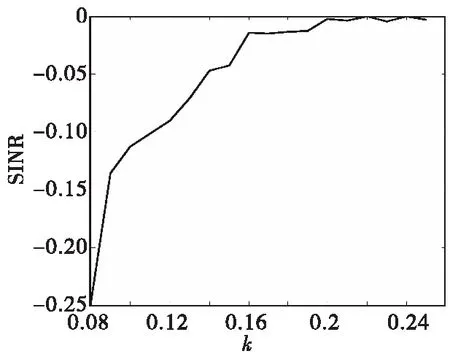
图9 E=0.08时信号信噪比随k变化曲线 Fig.9 Change curve of SINR with k when E=0.08

同理，根据图5中标注出的其余几个点的数据进行仿真(E1=0.08，K1=0.085 6)(E4=0.121;K4=0.085 6)(E5=0.16,K5=0.085 6)，信号自相关函数与能量谱密度对比图如图10、图11。

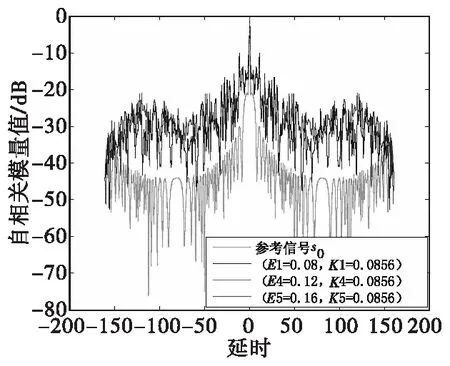
图10 信号的自相关函数仿真结果Fig.10 Simulation results of signal autocorrelation function

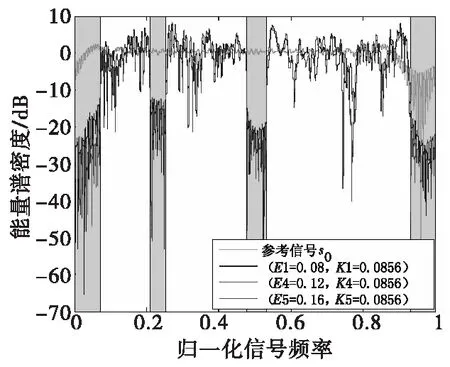
图11 能量谱密度比较效果图Fig.11 Comparison of ESD

从仿真图7—图11可以看出利用本文方法可以在指定的频段给出了一个很好的“频谱凹陷”，即能够有效地实现在该凹陷的频率范围实现与其他服务的共享，但仿真结果也说明，良好的频谱兼容特性是牺牲信号的自相关特性换取的。尽管如此，我们仍可以在一个合理的范围内，利用该方法找到频谱兼容特性和自相关特性尽可能好的恒模信号，图9显示，该方法得到的信噪比在E=0.08时图1给定的可行集区域内呈现上升趋势，进一步说明的该方法的有效性，曲线之所以不是十分平滑，是因为在该方法在具体执行过程中利用高斯随机化方法生成信号具有随机性造成的。在计算复杂度方面，该方法既涉及求解SDP问题，同时也涉及迭代算法，而求解SDP问题复杂度要远高于后者复杂度，此外计算复杂度也与高斯随机化方法生成信号的次数有关。

4 结论

本文提出了共享频谱雷达恒模发射波形设计方法。该方法的主要思想是针对恒模要求等约束条件利用凸优化手段建立数学模型，分析可行集并将非凸问题松弛成为可解的SDP问题。然后利用高斯随机化方法生成优化信号，但是由于松弛之后的问题模型偏离初问题比较明显，得到的解在指定的频段频谱密度仅下降10 dB左右，进一步利用迭代算法(IA-CPC)控制相似性参数得到频谱兼容特性更好的信号。仿真结果表明，利用本文提出的方法得到的优化信号在指定频段频谱能量下降明显，效果理想，能够很好地实现雷达与通信共享频谱。该方法涉及的计算复杂度仍较高，下一步研究方向是对现有方法进行改进、优化，以降低算法复杂度。