基于三次样条插值实现无人机高动态运动轨迹插值
高晓,杨志强,库新勃,郑蓉
(1.长安大学 地质工程与测绘学院,陕西 西安 710054;2.中国电力工程顾问集团西北电力设计院有限公司,陕西 西安 710032)
0 引 言
传统高分辨率航空摄影测量存在两个难以解决的问题,一是原始数据时效性差,二是新测数据耗时较长,难以满足工程进度需求[1].作为新型航空摄影测量技术,无人机航摄技术具有机动性好、灵敏度高、作业成本低、生产周期短等特点[2-4],在小区域或飞行困难地区高分辨率影像快速获取方面具有显著优势[5-6],已成为航空遥感领域的崭新发展方向.
无人机高精度航摄的基础是高精度的空中三角测量,即利用一定数量、分布密度的地面控制点实现影像元素的绝对定位[7].但在环境复杂区域,地面控制点难以布设或分布不均匀,导致无人机航摄影像数据处理的质量难以满足要求[8].随着定位定向系统(POS)的不断完善,无人机机载POS的条件已经成熟,用户可基于机载POS的差分全球卫星导航系统(GNSS)模块进行高动态、高精度定位,辅助影像空三加密,实现少像控或免像控的高精度影像处理[9-10].无人机机载POS中GNSS模块的采样频率一般为20~50 Hz,更高的采样频率对GNSS模块的软硬件要求过高,进而导致其市场价格激增,不利于无人机航摄系统的应用推广.因此,针对GNSS模块采样频率有限的问题,本文基于三次样条函数实现无人机高动态定位的高精度插值,并通过实测数据检验不同三次样条插值函数的异同,确定适用于无人机高动态定位的三次样条插值函数.
1 三次样条插值算法
为了保证插值算法的效率,同时避免无人机运动轨迹细节的缺失,可采用分段低次多项式代替单一多项式,其基本做法是将整个插值区间划分为若干个子区间,在每个子区间作低次插值多项式,然后将所有的子多项式拼接为一个整体多项式[11].分段低次插值算法的优点在于公式简单、运算速度快、稳定性好,但缺点在于节点处的导数不连续,导致插值函数失去光滑性.为此,三次样条插值函数应运而生[12-13].
1.1 三次样条插值
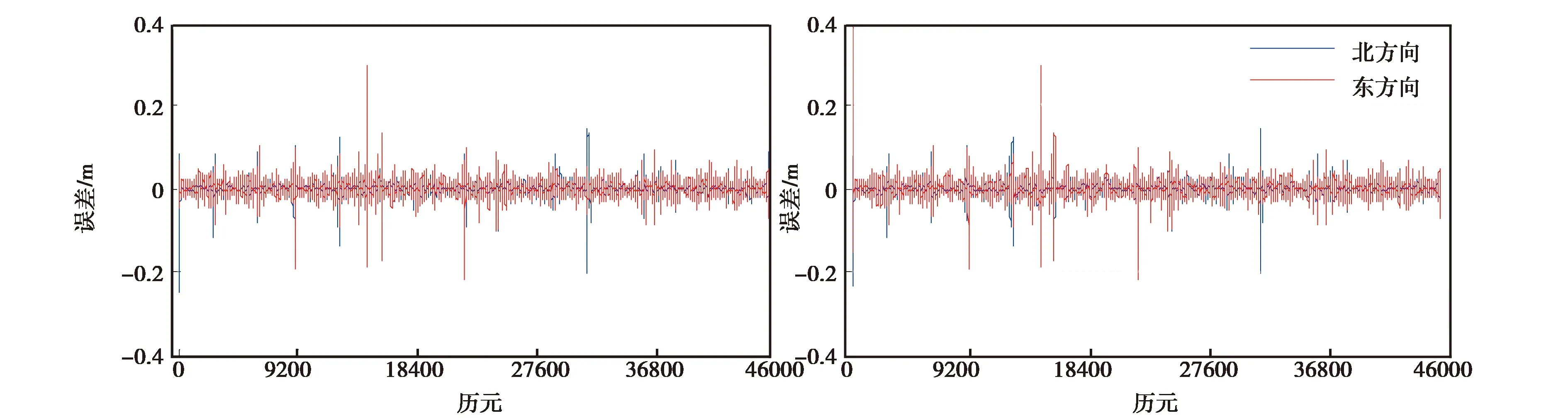
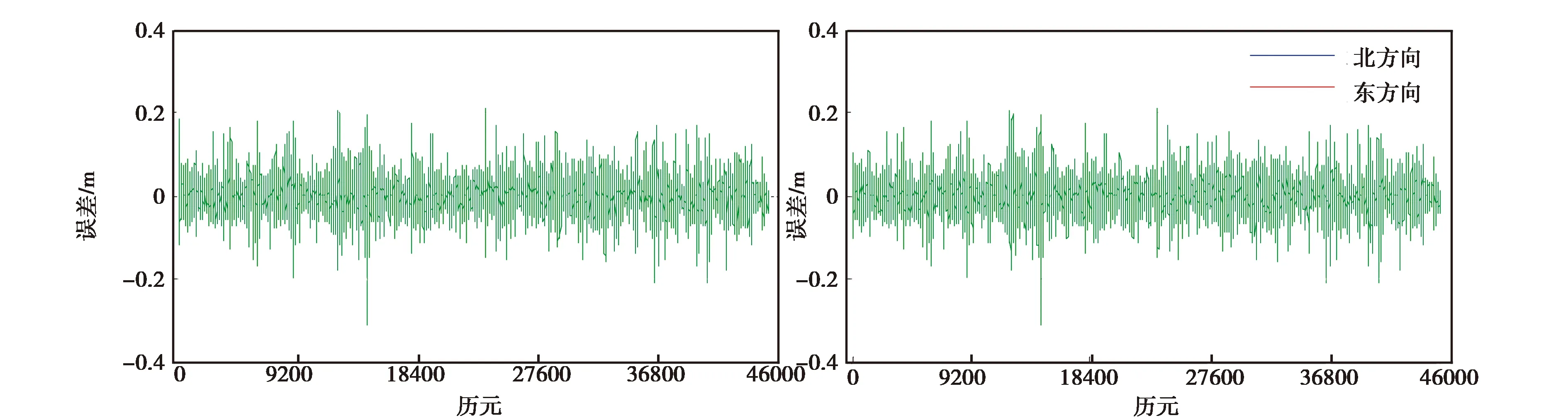
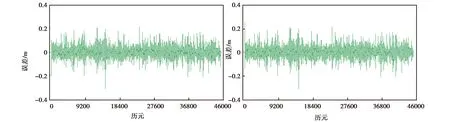
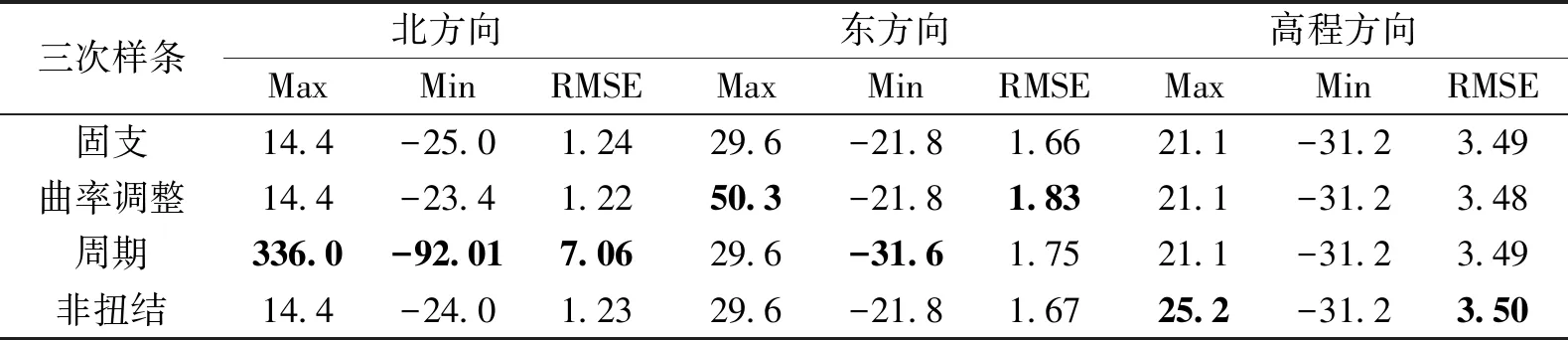
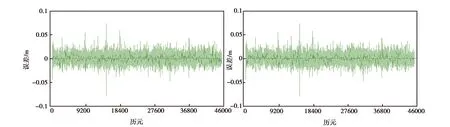
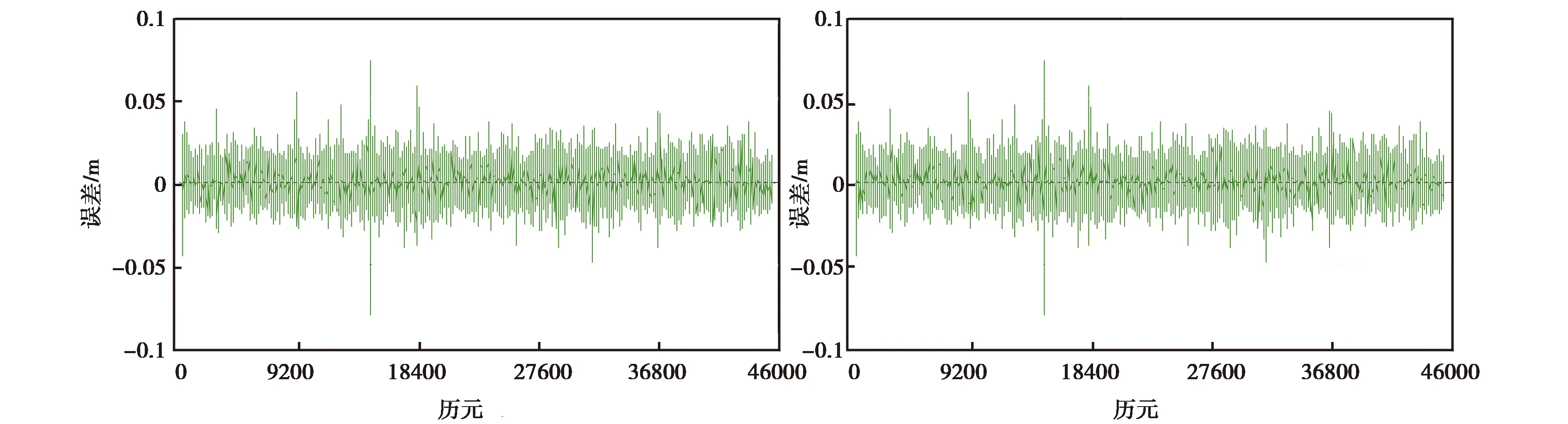
设区间[a,b]内给定一个节点划分:a=x0 s(xj)=yj,i=0,1,…,n. (1) 则称这个三次样条函数s(x)为三次样条插值函数. 如果s(x)是原始函数的三次样条插值函数,还需满足以下条件: s(xi-0)=s(xi+0), (2) s′(xi-0)=s′(xi+0), (3) s″(xi-0)=s″(xi+0). (4) 式中,i=1,2,…,n-1.式(2)~(4)则为三次样条函数需满足的连续性条件.三次样条插值函数是基于分段低次插值思想进行数据插值,由于插值次数较低,待定系数容易求解,插值速度较快.同时,分段插值可有效避免Runge现象发生,可较好地描述大部分光顺曲线,在工程中具有广泛的应用. 由于s(x)在每个子区间都是不大于三次的插值多项式,则每个子区间有4个未知参数.子区间数量为n,即未知参数总数为4n.由公式(1)~(4)可知,插值条件与样条条件仅提供4n-2个条件,因此,需要增加2个已知条件才能解算未知参数.通常采用端点约束的方式增加已知条件,即边界条件[14].根据边界条件的不同,三次样条函数可分为以下四类. 1.2.1 固支样条 固支样条的边界条件是已知首末端点的一阶导数,即 (5) 1.2.2 曲率调整样条 该样条函数的边界条件是已知首末端点的二阶导数,即 (6) 曲率调整样条的特殊情况为端点处的二阶导数恒为零,又称为自然样条函数,即 (7) 1.2.3 周期样条 周期样条要求样条函数及其导数是以端点区间长度为周期的函数,即 (8) 1.2.4 非扭结样条 该样条函数的边界条件要求样条在开始与结束两个子区间三阶导数相同,即 (9) 采用飞马固定翼无人机(F200)在陕西省渭南市东北部进行航空摄影测量,时间为2018年9月6日,飞行范围为4 km2(2 km×2 km),平均航高350 m,飞行时长58 min(GPST:04:39-05:37),数据处理时忽略无人机起降阶段.飞控平台GNSS模块自动采集动态GNSS观测数据,地面固定基准站同步采集GNSS静态观测数据,采样频率20 Hz,卫星截止高度角为10°,采用天宝数据处理软件(Trimble Business Center 4.0)进行GNSS动态后处理,共计45 420历元. 为对比不同样条函数的异同,对GNSS动态解算结果进行数据抽稀处理(抽稀后数据频率1 Hz,共计2 271历元).分别采用不同的三次样条函数对抽稀后的三维坐标值进行数据插值(插值间隔0.05 s),插值后数据量与原始动态解数量一致.以原始定位解坐标为真值,通过计算插值结果与真值的差值获取不同样条插值函数的误差序列. 图1为不同样条函数平面方向插值结果的误差序列图,图1(a)、(b)、(c)、(d)分别为固支样条、曲率调整样条、周期样条与非扭结样条的插值误差图.由图1可知,由于四种插值函数均为三次样条函数,插值思想基本一致,四种函数的平面误差序列具有很高的一致性,仅在部分历元有细微差别,最显著的区别在端点处.由于边界条件选取的不同,其端点处的插值结果有明显差异,尤其是曲率调整样条与周期样条,其端点插值误差大于0.4 m.分析原因,曲率调整样条要求函数在端点处二阶连续,周期样条要求函数以端点间距为周期,这两项要求与无人机实际运行轨迹难以相符,导致其平面插值误差在端点处显著增大.需要注意的是,由于飞行当天有阵风影响,部分历元无人机抖动异常,当数据间隔抽稀至1 s时,插值函数难以精确地反映该异常轨迹,导致部分历元的插值误差有所增加,但其数值一般小于0.2 m. (a)固支样条 (b)曲率调整样条 (c)周期样条 (d)非扭结样条 (a)固支样条 (b)曲率调整样条 (c)周期样条 (d)非扭结样条 图2为不同样条函数高程方向插值结果误差序列图.同样,由于四种插值函数均为样条函数,其插值的高程误差序列具有明显的一致性,除端点处有显著差异外,仅在少数历元有细微差别.同样,由于阵风影响,部分历元误差值明显增大.对图1、2的误差序列进行统计,结果如表1所示. 表1 不同三次样条函数插值序列误差统计结果 cm 三次样条北方向东方向高程方向 MaxMinRMSEMaxMinRMSEMaxMinRMSE 固支14.4-25.01.2429.6-21.81.6621.1-31.23.49 曲率调整14.4-23.41.2250.3-21.81.8321.1-31.23.48 周期336.0-92.017.0629.6-31.61.7521.1-31.23.49 非扭结14.4-24.01.2329.6-21.81.6725.2-31.23.50 表1示出了不同三次样条函数三维方向误差统计结果,包括误差极值(极大值和极小值)与均方根误差(RMSE).由表可知,周期样条在平面方向有异常误差,联系图1可知,由于端点处要求满足周期性边界条件,而实际飞行轨迹不满足周期性特征,导致其端点插值结果明显有偏.同样,曲率调整函数要求函数在端点处二阶连续,亦不符合飞行轨迹的实际特性,在端点处东方向有异常误差.由于端点处误差值明显偏大,导致RMSE值有所增加.固支样条与非扭结样条结果基本一致,无明显差别,水平方向RMSE值优于1.8 cm,高程方向RMSE值优于3.5 cm. (a)固支样条 (b)曲率调整样条 (c)周期样条 (d)非扭结样条 (a)固支样条 (b)曲率调整样条 (c)周期样条 (d)非扭结样条 为研究采样频率对三次样条插值的影响,对原始GNSS动态解再次进行抽稀处理(抽稀后数据频率5 Hz),同样采用不同样条函数对抽稀后的三维坐标序列进行插值(插值间隔0.05 s),以原始定位解为真值,计算不同插值结果与真值的差值,平面误差序列与高程误差序列分别如图3与图4所示. 由图3和图4可知,当给定数据频率为5 Hz,要求插值频率为20 Hz时,三次样条函数插值结果三维方向的精度均明显提高,除端点处存在异常误差外,其他历元平面插值误差一般小于2 cm,高程方向插值误差一般小于5 cm.由误差序列统计结果可知,水平方向插值误差RMSE值优于0.33 cm,高程方向插值误差RMSE值优于0.72 cm.以“三倍中误差”作为极限误差,固支样条与非扭结样条的平面插值精度优于1.0 cm,高程插值精度优于2.2 cm,其插值精度优于周期样条和曲率调整样条函数. 对比图1~2与图3~4,随着初始数据采样频率的增加,三维方向插值精度显著提升.由于插值思想基本一致,不同样条函数插值结果基本一致,差别主要集中于端点处,其主要原因在于不同样条函数对应的边界条件不同.由于曲率调整样条与周期样条的边界条件明显不符合无人机飞行轨迹特性,固支样条与非扭结样条插值精度优于前两者.鉴于非扭结样条要求起始子区间函数有三阶导数,该边界条件的实现难度明显高于固支样条的边界条件,因此,固支样条更适用于无人机高动态定位数据插值. 差分GNSS辅助空中三角测量技术可实现无人机影像元素的高精度绝对定位.由于无人机GNSS模块采样频率有限,更高频率的数据采集对GNSS模块软硬件提出更高的要求,不利于无人机的推广使用,因此,数据插值成为无人机高动态定位数据处理的重要环节.鉴于无人机飞行轨迹的特点,分段低次插值函数成为首选.本文研究了三次样条插值函数的基本原理,并对不同的三次样条插值函数进行了对比分析.采用无人机实测数据进行数据处理,对比不同样条函数插值结果与原始动态解的差异,结果表明,固支样条与非扭结样条函数的插值精度优于曲率调整样条和周期样条.由于非扭结样条的边界条件要求更高,无人机实际应用中建议采用固支样条.同时,样条函数的插值精度随原始数据采样频率的增加而提高,当原始数据采样频率高于5 Hz时,平面插值精度优于1.0 cm,高程插值精度优于2.2 cm,可满足无人机高动态定位的精度需求.1.2 边界条件
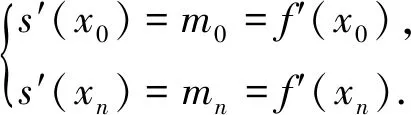
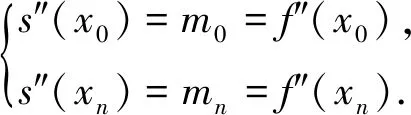
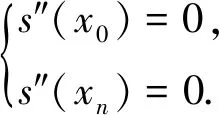
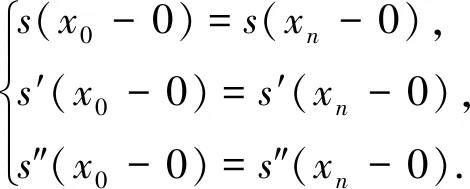
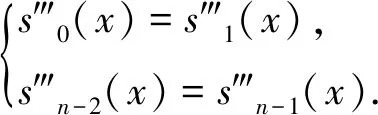
2 数据处理与结果分析


3 结束语

