载波相位平滑时间常数对GBAS精度增强的影响

倪育德,陈楚佳

(1. 中国民航大学 电子信息与自动化学院,天津 300300;2. 民航航空器适航审定技术重点实验室,天津 300300)

0 引 言

载波相位平滑伪距算法常被用来改善伪距差分定位的精度. 在实际应用中,载波相位平滑伪距多采用基于Hatch滤波的递推模型[1],平滑时间常数决定了滤波总误差的相对权重,是影响陆基增强系统(GBAS)定位精度的重要参数. 尽管Hatch平滑滤波器可以改善伪距的精度,减少噪声影响,但由于电离层和多径的影响,滤波后的误差存在发散现象[2]

为了减小电离层和多径引起的误差,提高GBAS的定位精度,许多研究人员一直致力于提高传统Hatch滤波器的性能. McGraw[3-4]设计了两种双频滤波方法,分别为无发散(D-free)滤波方法和无电离层(I-free)滤波方法. 然而Konno[5]指出,这两种方法均存在不同程度的缺陷,无法消除严重电离层的影响. McGraw等[6]又提出一种具有柔性平滑窗口的Hatch滤波方法,但该方法也会面临着严重电离层风暴的影响.

国际民航组织(ICAO)2018年颁布的第七版“附件10”中明确规定[7],I类及II/III类GBAS精密进近所要求的载波相位平滑时间常数分别为100 s和30 s. 但是ICAO推荐的平滑时间常数综合考虑了多种影响GBAS精度的因素,其中包括滤波、伪距测量精度、大气误差等. 关于这些因素对GBAS定位精度影响的专项分析“附件10”并没有给出. 本文结合 “附件10”和美国航空无线电技术委员会(RTCA)的相关标准[7-9],分析研究不同载波相位平滑时间对电离层时空梯度的影响,在不改变Hatch滤波结构的前提下,从所构造的滤波总误差方差出发,推导出同时降低电离层和多径影响的加权因子,进而推出最优的自适应平滑时间,并与ICAO规定的精密进近平滑时间进行比较,分析不同平滑时间给定位精度带来的影响.

1 GBAS载波相位平滑伪距差分修正算法

GBAS定位所使用的关键技术之一是载波相位平滑伪距差分技术,是一种提高定位精度的重要手段. 接收机通过载波相位观测量定位比通过伪距观测量能获得更高的测量精度,但这种方法的最大缺陷之一是无法获得载波相位中所包含的整周数,通常称之为“整周模糊度”. 为了平衡两种方法,利用载波相位测量值辅助码相位测量从而提高测距精度[10]. 差分修正过程如图1所示.

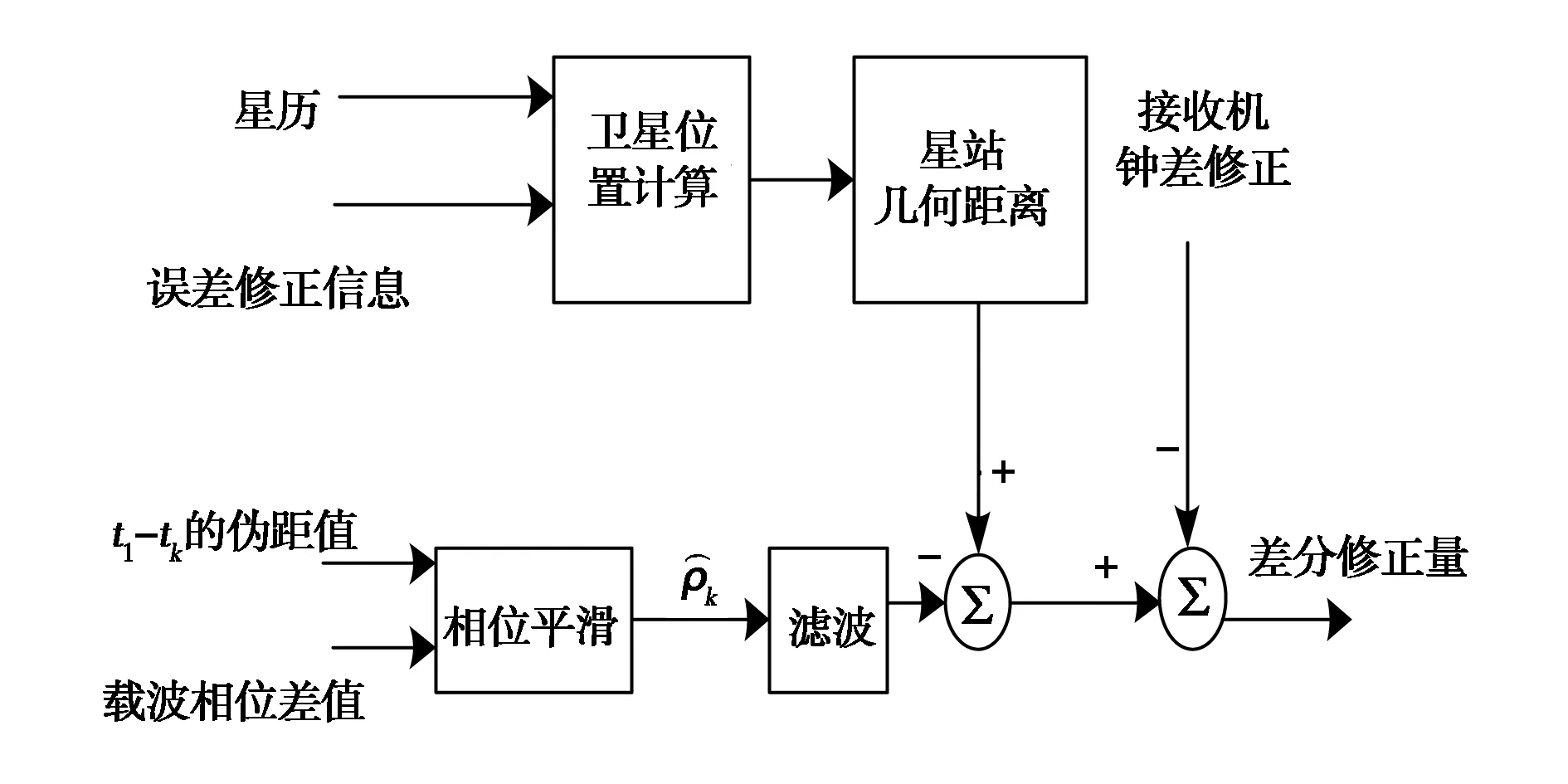
图1 载波相位平滑伪距差分修正过程

由图1所示，一种既无模糊度又相对平滑的伪距测量值为

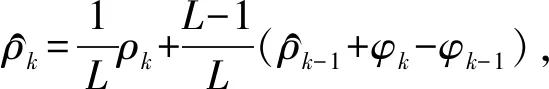
(1)

由式(1)可知,各历元的平滑伪距与滤波步长L有关,同时权重1/L受到载波平滑时间常数τ的限制[11]. 一般情况下,限定τ的原因在于,载波相位平滑伪距会引入随历元k增加的电离层发散误差. 如果不对1/L加以限制,电离层发散误差最终会超过载波对伪距误差的减缓效果. 因此,载波相位平滑时间常数是影响载波平滑伪距精度的重要参数.τ取值太小,会影响平滑对伪距误差的减缓效果;τ取值太大,则会引入过多的电离层发散误差.

2 平滑时间常数对GBAS定位误差的影响

2.1 电离层延迟误差

为研究方便,把码伪距和相位测量的关键部分表示为

ρk=Rk+Ik+εk,

φk=Rk-Ik+Nk+ηk.

(2)

式中:Rk为接收机到卫星的真实距离;εk和ηk分别为码测量和载波测量的随机噪声.

由于时钟偏移和对流层延迟具有很强的空间相关性,可以在差分过程中消除,讨论中忽略它们[12]. 因此,εk和ηk将被认为是多径误差.

载波相位平滑过程中产生的平滑误差ek为

(3)

结合式(1)和式(3),平滑误差动态方程为

(4)

电离层引起的误差包括时间和空间电离层延迟的影响[13]. 为方便讨论,将相邻历元间的电离层延迟用时间梯度和空间梯度表示为

(5)

式中:假设机载用户和地面监测站的电离层延迟分别为Ia和Ib；V为机载接收机飞行速度;kt和ks分别表示电离层延迟时间梯度和空间梯度,与卫星仰角有关.

因此,式(4)可以表示为

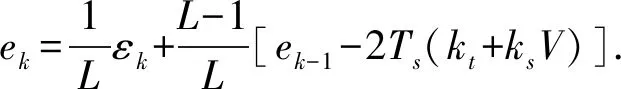
(6)

结果表明,平滑误差与接收机速度、电离层时间和空间梯度以及多径有关.

由式(5)和式(6)可得历元tk的累积误差Ek为

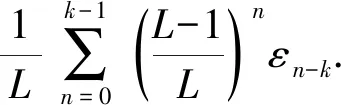
(7)

可以看出,平滑误差包含电离层诱导误差和多径误差的双重影响. 因此,平滑时间对加权因子的影响以及对减小滤波总误差具有重要意义.

当Hatch滤波器达到稳定状态时,不考虑多径和其他因素,可以得到平滑电离层延迟稳态误差eiono为

eiono=-2Ts(kt+Vks)(L-1)

=-2(τ-Ts)(kt+Vks).

(8)

设机载接收机与GBAS基准站二者之间倾斜距离为X,则

Ia-Ib=ksX.

(9)

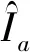
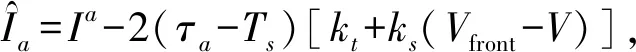
(10)

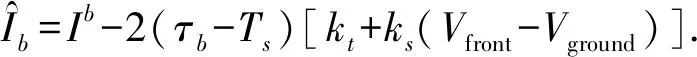
(11)

式中:τa、τb分别为GBAS机载接收机和地面基准接收机的平滑时间常数;Ts为采样周期.

将二者相减,得残余电离层延迟误差为

ks[X+2(τa-Ts)V].

(12)

2.1.1 平滑时间对电离层时间梯度的影响

在电离层时间梯度的讨论中,暂不考虑电离层空间梯度和时间梯度初始值等因素,可以得到时间梯度对载波平滑过程的影响,滤波器误差渐近于一个常数偏移量,当达到稳态时可以表示为

θt=2(τa-τb)kt=2τkt.

(13)

式中各参数含义与上文相同. 可以预料,当飞机遇到强烈的电离层风暴时,这种误差可能大得多.

RTCA 2004年颁布的《局域增强系统最低运行性能标准》(DO-245A)[9]规定,垂直电离层空间梯度的标准偏差为2～5 mm/km,典型值为4 mm/km,最大电离层时间梯度为10 mm/s. 在仿真实验中,假设电离层时间梯度为5 mm/s,采用天津滨海国际机场34L跑道3°理想下滑道上的最后进近点[N39.205,E117.297,600 m]作为用户位置,卫星遮蔽角为5°. 计算时长4000 s,采样间隔50 Hz. 分别选取30 s、100 s、200 s以及400 s的平滑时间常数. 图2示出了不同的时间常数下,电离层时间梯度对滤波误差的影响. 结果表明,随着平滑时间常数的增大,滤波误差也会增大,并且误差逐渐趋于一个稳定值.

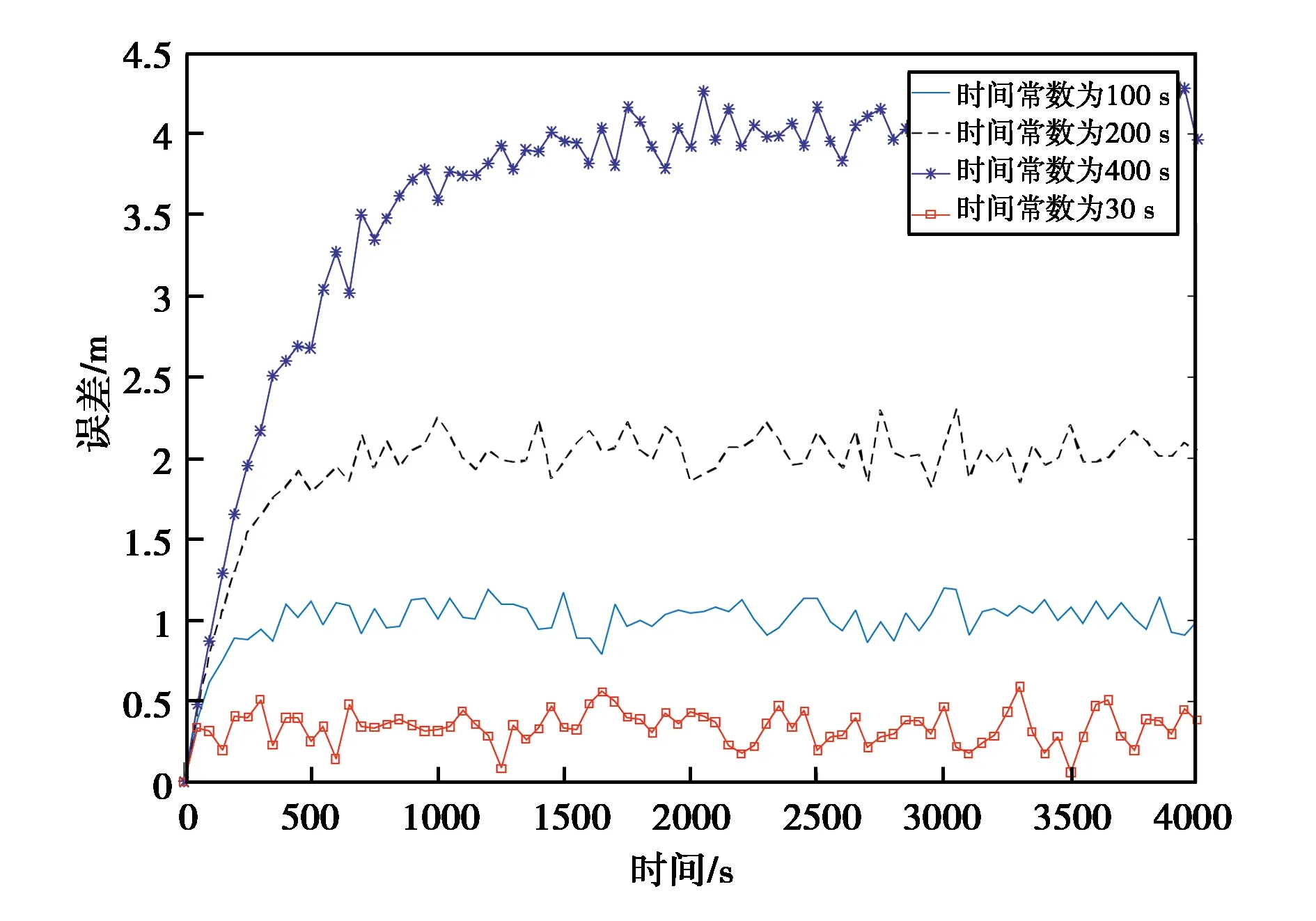
图2 电离层时间梯度对载波平滑伪距的影响

2.1.2 平滑时间对电离层空间梯度的影响

同样,不考虑时间梯度和空间梯度初始值等因素,只考虑空间梯度,得到空间梯度对载波平滑过程的影响,当达到稳态时,滤波误差可表示为

θs=ks[X+2(τa-Ts)V]=2τVks.

(14)

式中其他各参数含义与前文相同.

式(14)表明电离层空间梯度对快速运动的用户影响更大,但对静止的用户没有影响.

图3示出了不同平滑时间下电离层空间梯度对滤波误差的影响.在实验中,机载接收机航迹采用由天津滨海国际机场着陆入口点[N39.111,E117.354,3.7 m]、着陆入口点高度15 m所确定的3°理想下滑道,飞机速度为150 m/s,电离层空间梯度为4 mm/km. 计算时长4000 s,采样间隔为50 Hz. 仿真结果显示,平滑时间越大,电离层空间梯度产生的滤波误差也越大.

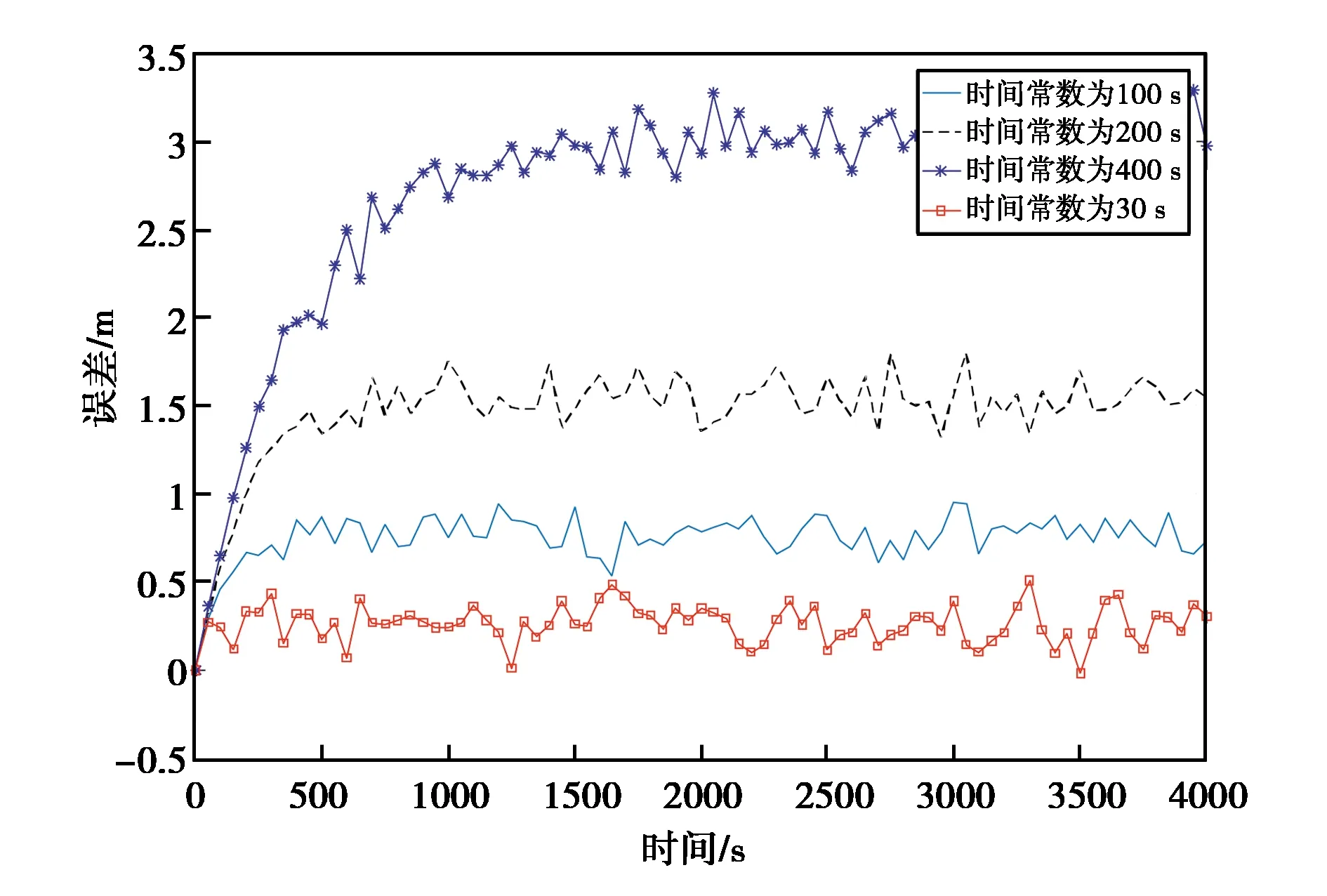
图3 电离层空间梯度对载波平滑伪距的影响

从上述分析不难看出,电离层时间梯度和空间梯度都会对Hatch滤波产生影响,出现稳态误差或者残差. 平滑时间越大,产生的误差也更大.

2.2 总滤波误差

由式(7)可知,稳态误差由电离层引起的误差、多径和加权因子多个因素决定. 可以通过选择最优加权因子来抑制电离层和多径诱导的滤波误差. 为方便计算,设

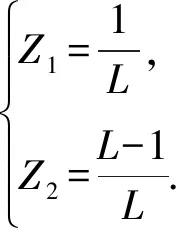
(15)

根据式(7)结果,滤波后的总误差可写成

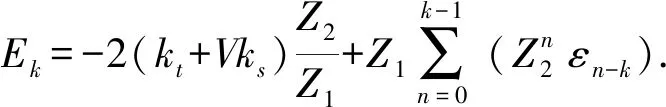
(16)

2.2.1 静态定位总滤波误差

在静态定位时,接收机的速度为零,因此由电离层引起的静态误差方差为

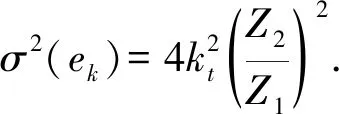
(17)

静态定位中的多径误差ε可以建模为有限多个准正弦波的加权和[14],即

ε=Amcos(ωt+φ).

(18)

其中:Am为多径振幅， 与卫星仰角有关;ω为频率;φ为初始相位.

因此多径诱导的累计误差为

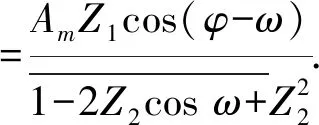
(19)

由于eε≤Am,载波过程抑制了多径,平滑后的多径误差方差为

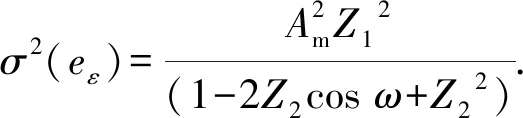
(20)

因此,经过滤波的静态定位总误差方差可表示为

σ2=σ2(ek)+σ2(eε)

(21)

只有当权重因子Z1、Z2满足式(22)时,总误差方差达到最小．

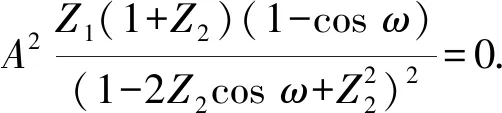
(22)

图4示出了静态定位时多径对滤波的影响,图5示出了经过滤波的电离层时间梯度和多径振幅的总误差方差. 仿真实验中,ω设置为0.06 rad/s,多径信号幅值为0.22 m,采样频率为50 Hz,电离层时间梯度为5 mm/s,计算时长4 000 s,静态位置点

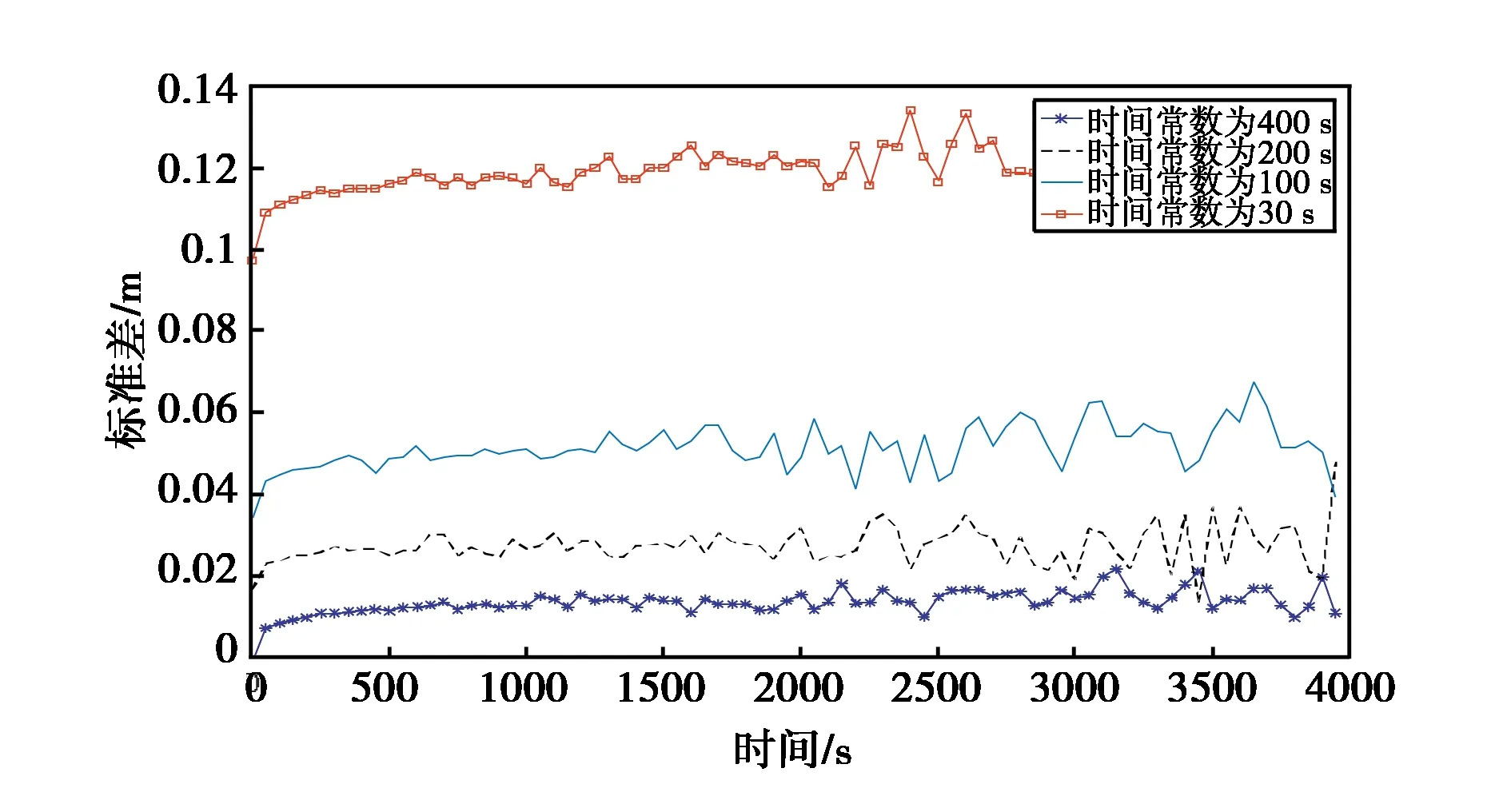
图4 静态定位多径误差标准差

图5 静态滤波总误差

坐标为 [N39.205,E117.297,600 m]. 图4的仿真结果表明,采样时间一定时,平滑时间常数对多径误差的影响与电离层的正好相反,多径误差随着平滑时间的减小反而增大.

图5示出了静态环境下的滤波总误差,电离层时间梯度和多径振幅越大,滤波误差越大.

2.2.2 动态定位总滤波误差

动态定位时要考虑电离层空点梯度以及接收机速度带来的影响,则平滑后的电离层误差为

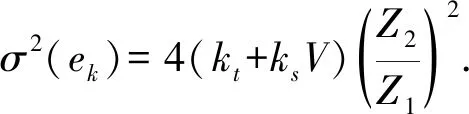
(23)

式中的参数含义与上文相同.

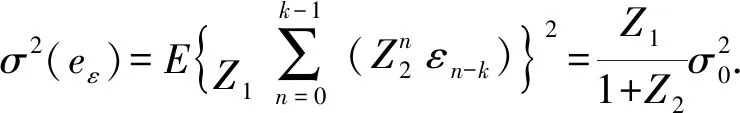
(24)

则动态定位的滤波总误差为

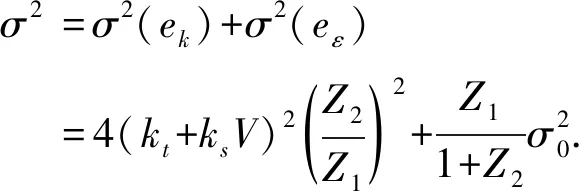
(25)

只有当权重因子满足下式时,总误差方差达到最小

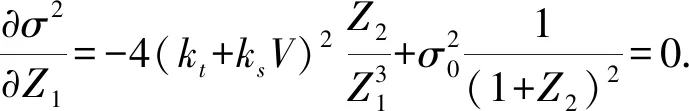
(26)

图6和图7示出了运动定位下,电离层空间梯度和多径标准偏差影响的总滤波方差,仿真中将机载运动速度设为150 m/s,除飞机速度外,仿真条件与2.1.2节一致. 图6表明,动态条件下,平滑时间越大,多径对滤波的误差越小.

图6 动态定位多径误差标准差

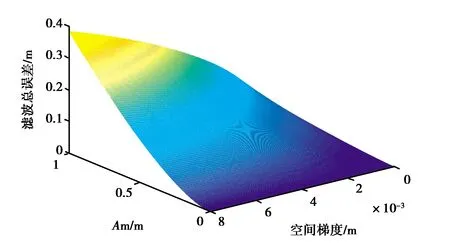
图7 动态定位滤波总误差

从图7可以看出,动态定位下,随着电离层空间梯度和多径振幅的增大,滤波后的总误差也显著增大.

3 最优平滑时间对GBAS定位精度的影响

由式(25)总滤波误差可推算出电离层延迟误差和多径误差的最佳权重,从而得到自适应的最优平滑时间.

如前所述,用户到基准站的距离、卫星仰角、电离层梯度、多径误差等都是最优平滑常数所依赖的决定因素. 理论上每一时刻都有一组对应的最优平滑时间值. 在对GBAS定位进行仿真过程中,分别将最优平滑时间与ICAO相关标准中推荐的平滑时间进行比较,验证该算法的有效性.

正常情况下,电离层时间梯度不超过10 mm/s,为更好比较最优平滑时间常数对GBAS定位精度的影响,仿真实验的采样频率设为1 Hz,电离层时间梯度设为5 mm/s,电离层空间梯度设为4 mm/km,ω设置为0.06 rad/s,Am为0.5,计算时常为2000 s. 得到的最佳权重为Z1=0.0069,Z2=0.9931. 从而推出最优时间常数为

(27)

结合上述设置的条件,分别从静态和动态两种环境下讨论平滑时间对GBAS定位精度的影响.

3.1 GBAS定位静态仿真

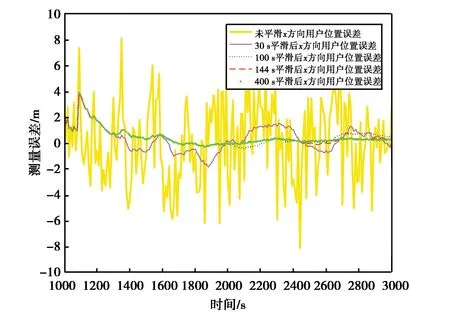
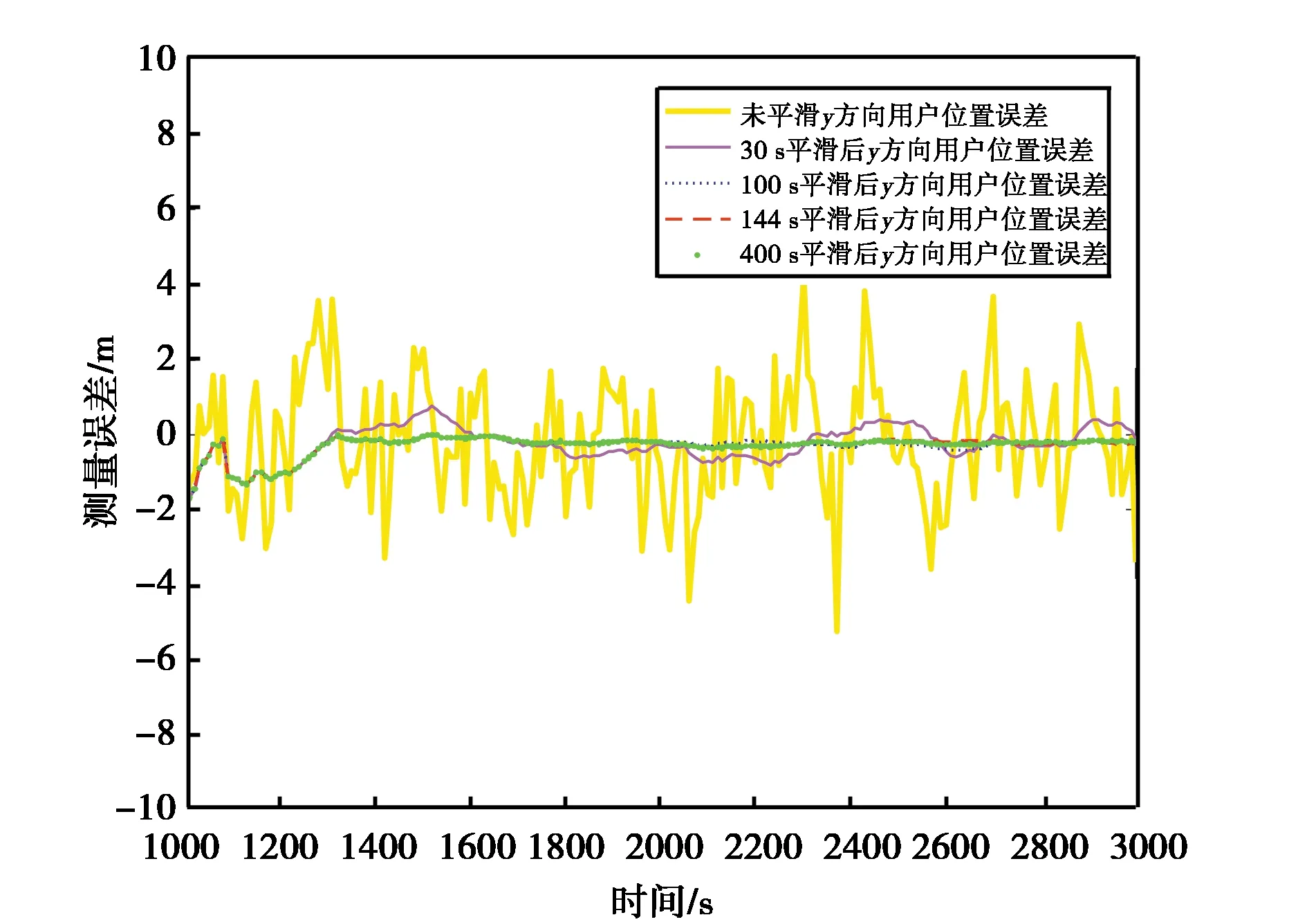
仿真采用美国海岸警卫队导航中心提供的第1000周GPS历书数据(2018年10月). GBAS地面站基准接收机的三维位置分别为[N39.118,E117.350,3.78 m]、[N39.117,E117.350,3.79 m]、[N39.118,E117.351,3.78 m]和[N39.117,E117.351,3.80 m]. 静态观测位置为天津滨海国际机场34L跑道3°理想下滑道上的最后进近点

(a)x轴方向定位误差

(b)y轴方向定位误差

(c)z轴方向定位误差

[N39.205,E117.297,600 m],电离层时间梯度设为5 mm/s,采样时长为3000 s.

图8(a)、(b)、(c)示出了GBAS在不同平滑时间下的X、Y、Z三个方向上的定位误差.

为了直观反映定位状况,图9示出了不同平滑时间下,GBAS水平方向上的定位误差.

从图8和图9可以看出,通过最佳权重推出的最优平滑时间常数与ICAO规定的平滑时间相比,定位误差更接近于零,并且误差在2 m以内,定位精度得到提高.

3.2 GBAS定位动态仿真

GBAS动态定位采用飞机从成都双流机场飞往天津滨海国际机场的快速数据存取记录器(QAR)中的数据,实验提取了飞机在天津滨海国际机场3°下滑道上的160个下滑点,电离层空间梯度设为4 mm/km,采样频率为1 Hz. 其他仿真条件与2.2.2节一致. 图10为飞机的下滑轨迹图.

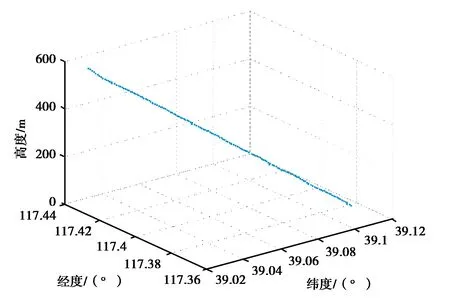
图10 飞机最后160 s的QAR下滑轨迹

图11和图12分别示出了动态环境下,不同平滑时间对GBAS水平和垂直方向上定位精度的影响.从图中可以看出,在设置好各类参数的条件下,推出的最优平滑时间定位误差范围最小. 误差大多被其他时间范围覆盖,集中于零点附近.

图11 动态条件下的水平方向定位误差

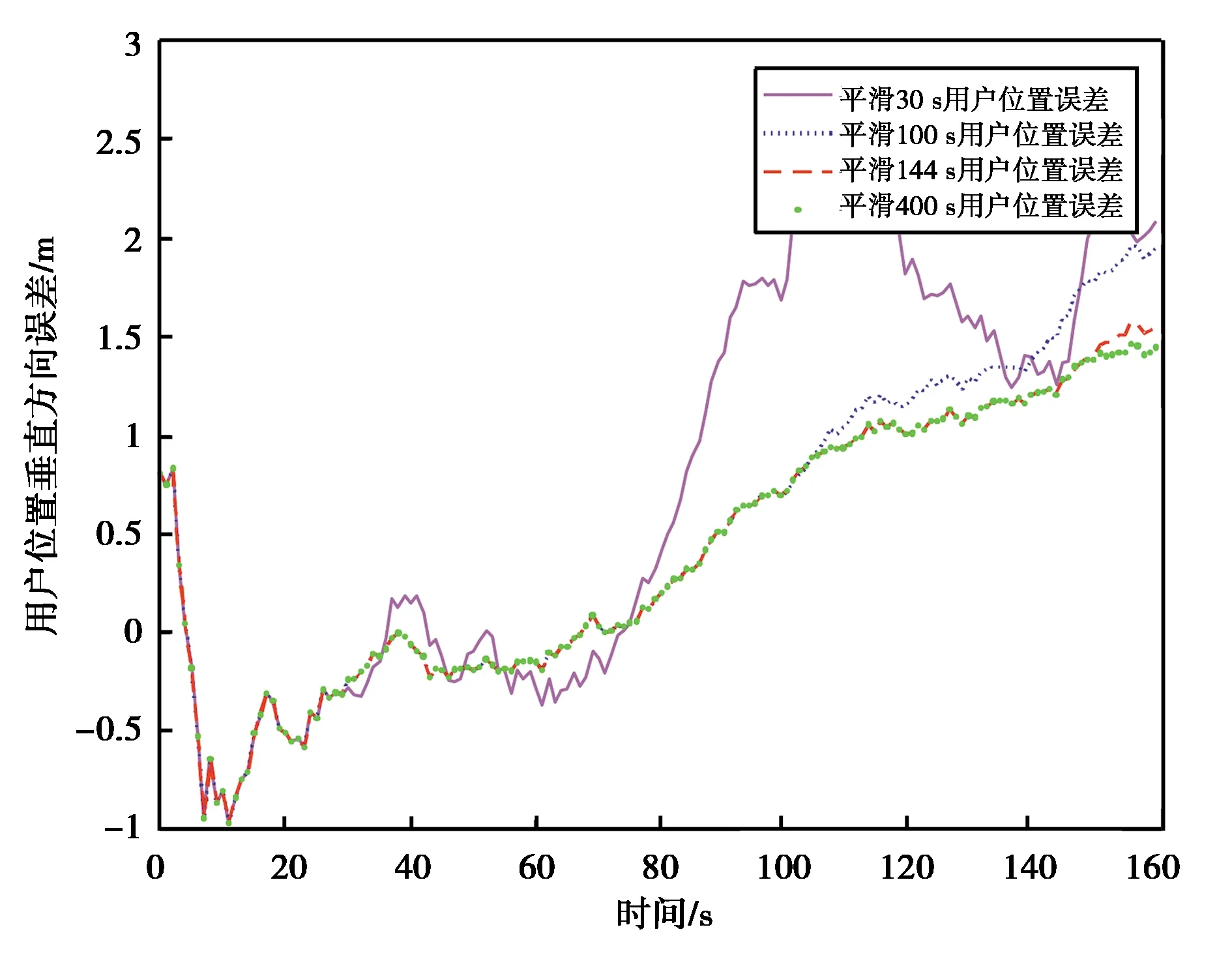
图12 动态条件下的垂直方向定位误差

3 结束语

本文通过研究载波相位平滑伪距算法,重点分析了滤波误差对GBAS定位精度的影响,通过研究Hatch滤波过程中产生的电离层和多径误差,给出了自适应最优平滑时间的解算过程,并仿真了不同平滑时间下的GBAS定位误差,可获得以下结论:

1) 电离层延迟误差和多径误差是影响Hatch滤波总误差的两个关键因素,电离层延迟误差和多径误差越大,滤波总误差也随之变大,选择最佳权重可以得到最小的滤波总误差;

2) 不同的平滑时间对电离层延迟和多径误差的影响正好相反,平滑时间越小,电离层延迟越小,但多径误差反而越大;

3) 在GBAS定位中,滤波误差是影响GBAS精度的一个重要因素．在单独考虑滤波因素的条件下,采用最佳权重推出的最优平滑时间比ICAO规定的平滑时间有更好的定位效果,可以满足II/III类精密进近的要求,定位误差最小. 将该算法应用于低成本的单频接收机,可以得到更精确的定位结果.