基于决策树集成的债券发行企业财务预警研究
宋宇 李鸿禧


【摘要】在我国,债券发行人中财务危机企业数量远小于财务健康企业,样本的非平衡性导致一般的财务预警模型在训练时对财务危机企业的特征挖掘不足、预警精度低。利用“聚类Bagging”集成方法,将样本数量较多的财务健康企业样本分成多组,将多组财务健康样本与财务危机样本进行两两配对,形成两类样本大致平衡的多个训练子集。在多个训练子集上分别构建决策树模型作为基学习器,使得决策树基学习器可以大致同等地学习健康样本与危机样本的特征。利用基学习器在测试集上的预测精度AUC值作为权重,对决策树基学习器进行加权,得到决策树集成模型,作为最终的财务预警模型。以制造业债券发行企业为样本,实证对比发现基于决策树集成的财务预警模型精度更高,说明本模型能够在总体预警正确率较高的前提下提高对财务危机企业的正确识别率。
【关键词】财务预警;决策树集成;AUC;预警指标体系;债券发行
【中图分类号】F830 【文献标识码】A 【文章编号】1004-0994(2020)06-0045-6
一、引言
随着债券市场规模不断扩张、债券品种逐渐多样化,债市信用风险越来越难以把控。2018年以来我国金融市场上的债务违约呈现常态化。2018年全年违约债券125只、违约规模高达1160亿元,超过2014 ~ 2017年之和。可见,我国金融市场的信用风险形势愈加严峻。在债券违约常态化的大趋势下,对债券发行人的财务风险及时进行预警显得尤为重要。财务预警是指通过挖掘企业数据和财务风险之间的关联关系,预测企业发生财务危机的概率。对债券企业进行财务预警,一方面能够提前给出风险信号,便于企业管理者及早改善经营,避免破产违约的发生;另一方面能够为银行、基金等机构提供投资决策参考,使其免遭巨额损失。
财务预警模型的现有研究大致可分为三类:
一是基于统计计量方法的模型,其中有代表性的方法包括判别、聚类、逻辑回归等。杨贵军等[1] 在财务预警体系中增加了Benford因子,并利用Lasso-logistic模型构建财务风险预警模型。张发明等[2] 利用Topsis-GRA方法构造动态信用评价加权决策矩阵,得到动态信用评价结果。周忆等[3] 基于卡尔曼滤波算法构建了僵尸企业风险动态预警模型。Mizen等[4] 利用次序Probit回归模型预测美国债券发行人的违约风险。
二是基于机器学习方法的模型,其中有代表性的方法包括决策树、支持向量机、神经网络等。蔡立新等[5] 在分析大数据技术与企业财务风险预警需求的基础上,构建了大数据视角下的企业财务风险预警机制。李茜等[6] 利用三种BP神经网络的改进算法构建财务预警模型,在预测精度上进行对比分析。Sevim等[7] 利用决策树、神经网络、逻辑回归建立了货币危机的预警系统。
三是基于多种方法的组合模型。杨胜刚等[8] 利用决策树方法对个人信用指标进行筛选,再利用神经网络构建分类模型。丁岚等[9] 以logistic回归、决策树、支持向量机作为初级学习器,以支持向量机作为次级学习器,预测P2P网贷的违约风险。Javier De Andrés等[10] 将模糊聚类和多元自适应回归模型结合,对企业的破产概率进行预测。
决策树模型的概念最早由Hunt等在1966年提出,最有影响力的模型是Quinlan提出的基于ID3算法的模型,其以信息增益选择结点分裂属性为基础。后来又提出了改进后的C4.5算法,其以信息增益比率选择属性为基础。而C5.0算法在C4.5算法的基础上又进一步提高了识别率。近年来,决策树C5.0算法在风险预警和信用评级方面应用广泛。庞素琳等[11] 将决策树C5.0算法用于构造银行个人信用评级模型。王茂光等[12] 通过决策树C5.0算法建立了小额网贷平台的风险监控模型。
上述决策树财务预警模型忽略了财务正常样本与危机样本之间数量比例不平衡的问题。在当前我国资本市场上,发生财务危机、资不抵债的融资企业(发债主体、借款人等)仍是少数,大多数融资企业都处于财务正常状态。这种危机样本与正常样本数量不均衡的现象,会導致分类模型在训练时更多地学习正常样本的数据规律,而忽略了对危机样本的规律挖掘,从而对危机样本的预测精度过低。所以,本文在考虑债券发行人中财务危机企业数量远小于财务健康企业的这种非平衡数据特征的前提下,构建决策树集成模型,旨在解决非平衡数据特征下的信用危机预警问题,并提高预警的精度。
二、基于决策树集成的财务预警模型
集成学习是将多个机器学习模型(称为“个体学习器”)按照一定的方法集成到一起。经典的集成方法有AdaBoost、Bagging、随机森林,这些经典方法的特点是能让个体学习器保持差异化,以保证每个个体学习器都能反映不同的信息,集成后的结果能够更加全面,从而提升预测的精度。
本文采用的是同质集成,即集成中只包含同种类型的个体学习器,此时的个体学习器称为“基学习器”。本文采用决策树C5.0算法构建决策树基学习器,通过“聚类Bagging”方法将多个决策树基学习器进行集成,以解决非平衡数据特征下的财务预警精度问题。
(一)基学习器的构建
1. 决策树C5.0算法。决策树C5.0算法依据的是信息增益比率,选取该节点上信息增益比率最大的指标作为分裂变量,划分样本生成下一层新的结点。信息增益比率的计算过程如下:
其中,n(Sj)为样本子集Sj的样本数量,n为样本总数。条件信息熵E(S|X)反映了样本集合按照指标X的取值进行分类之后,对于财务危机的平均分辨能力。条件信息熵E(S|X)越小,指标X对于财务危机的分辨能力越强。
信息增益G(X)反映了指标X对于“是否发生财务危机”的分辨能力。信息增益G(X)越大,指标X对于“是否发生财务危机”的分辨能力越强,从而可以更准确地将财务危机样本识别出来。为了消除指标取值种类数目的影响,进一步计算信息增益比率R(X):
其中,n(Sj)为样本集合按照指标X取值划分后的样本子集Sj的样本数量,n为样本总数。
以上为信息增益比率的计算过程。以信息增益比率为关键参数构建一个决策树模型,步骤如下:
Step1:以样本全集作为决策树的根结点,计算全部评价指标的信息增益比率R(Xi)。选取信息增益比率最大的指标作为根结点的分裂变量。按照分裂变量的取值将样本分成若干个子集,每个子集作为下一层的一个结点。假设,指标“学历”为全部指标中信息增益比率最大的指标,选取“学历”为根结点上的分裂变量。根据“学历”指标下的四种取值{高中,本科,硕士及以上,其他}将样本分为四类,形成第二层的四个节点。
Step2:在决策树第二层中,对于每一个结点上的样本集合,计算在该样本集合上各个指标的信息增益比率,选择信息增益比率最大的指标作为当前结点上的分裂变量。同样,根据分裂变量的取值继续分裂成第三层上的结点。
Step3:以此类推逐层生成结点,直到满足如下三种情况之一时停止:①当前结点的样本集合中所有的样本都属于同一类别(在本研究中,同属于财务危机企业或财务正常企业),当前结点为叶结点。②当前结点的样本集合在所有指标上的取值均相同,无法进一步划分样本。此时,用当前结点上多数样本所属的类别标记当前结点,当前结点为叶结点。③当前结点包含的样本集合为空。用当前结点的父节点(该结点上一层直接关联的结点)中多数样本所属的类别标记当前结点,当前结点为叶结点。
2. 剪枝。由于在决策树的生成中,为了尽可能正确识别出财务危机企业,从而不断地划分样本,造成决策树过于庞大,对于训练样本拟合得过好,由此丧失了对于训练样本外新样本的预测能力。为了避免过拟合问题,本文采用EBP(基于错误的剪枝)方法,自下而上地对决策树的每个结点进行剪枝。其基本思路是,分别计算剪枝前后的预测错误率,若剪枝后的错误率相比剪枝前并没有明显增大,说明这个子树对于预测效果的影响很小,属于冗余的分枝,应该剪掉。
假设Tj为以结点j为根的子树,剪枝前的叶结点是子树Tj的叶结点,剪枝后以结点j作为叶结点。采用悲观错误率计算方法,计算剪枝前后该子树上样本的预测错误率e1、e2。假设样本预测错误率是一个服从二项分布U(e,n)的随机变量。给定一个置信度CF,可以求出关于错误率的一个置信区间[LCF,UCF]。若剪枝后的错误率期望值n×e2小于剪枝前的错误率上分位点UCF,说明剪枝后的错误率相比剪枝前并没有明显增大,那么剪枝;否则不剪枝。置信度CF越大,则剪枝越严重,CF一般取0.75。
(二)决策树集成
市场上的债券发行人绝大多数都是财务健康的企业,而发生财务危机的不良发行人不足5%,两类样本的数量极其不平衡。这种情况会导致决策树模型在训练时更多地学习财务健康企业的数据特征,而忽略了对财务危机企业的特征挖掘。这种现象被称为非平衡样本问题。
本文基于“聚类Bagging”集成方法,通过K均值聚类的方法,将数量较多的财务健康企业样本分成K组,将K组财务健康样本与财务危机样本进行两两配对,形成K个大致平衡的训练子集。在K个训练子集上分别构建决策树作为基学习器,然后再集成,形成最终的预警模型,从而解决财务预警模型构建过程中的非平衡樣本问题。具体的模型构建过程如下:
Step1:聚类。将样本划分为训练集和测试集,训练集是为了训练模型的样本集合,测试集是为了验证训练出的模型的预测精度。在训练集中,假设D为财务健康样本集,F为财务危机样本集。利用K均值聚类法将健康企业样本D分成K份{D1,D2,…,DK}。由于聚类方法的特性,可以保证各类样本之间的差异化最大,这样就保证了不同样本子集训练出的决策树基学习器具有差异性。
Step2:生成多个训练样本。将{D1,D2,…,DK}中每个集合与危机样本集合F进行两两配对,形成K个训练子集{D1∪F,D2∪F,…,DK∪F }。由于原本数量过多的健康样本集D被拆成了K份,每一份健康样本子集Di中样本数量大大减少,因此新形成的训练子集Di∪F中,健康样本数量与危机样本数量变得相对平衡,从而大大削弱了总体样本中的非平衡样本问题。
Step3:决策树基学习器。利用前文所述的方法,分别在上述K个训练子集上构造决策树,形成K个基学习器{M1,M2,…,MK}。聚类的方法特性使得不同训练子集之间具有差异性,保证了不同子集训练出的决策树基学习器具有差异性。
Step4:决策树集成。根据决策树基学习器的预测精度对基学习器进行加权,预测准确性越高,权重越高,从而形成决策树集成学习器。具体方法为:利用K个基学习器{M1,M2,…,MK}在测试集上进行预测,将预测结果与实际财务状态进行对比,画出ROC曲线。
ROC曲线的横坐标是伪正率,即预测为正例但实际为负的样本占所有负例样本的比例(在本文中“发生财务危机”是研究对象,为正例);纵坐标是真正率,即预测为正例且实际为正的样本占所有正例样本的比例。AUC值是ROC曲线与横坐标包围的面积,AUC值综合反映预测模型的准确度和灵敏度。以AUC值作为权重对决策树基学习器进行加权,得到决策树集成学习器,作为财务预警模型。
经过上述过程,将决策树基学习器集成,最终得到财务预警模型。上述过程如图1所示。
三、实证分析
1. 样本的选取。本研究选取我国2014 ~ 2018年有存续债的1159家制造业企业为实证样本。将这些债券发行人在2014 ~ 2018年中有债券存续年份的数据作为实证数据,数据来自Wind数据库。相同企业不同年份的数据可以看成不同的样本,共得到3858个实证样本。
本研究将以下两种情况标记为“企业发生财务危机”:一是债券发行人从违约前一年直至债券到期均标记为发生财务危机,这是由于绝大多数债券发行人在发生违约的之前一段时间,就已经因经营不善或投资失败出现资金流短缺等财务困境问题。二是对于上市公司的债券发行人,将标记?ST当年及前三年、ST当年及前两年均标记为发生财务危机,主要是因为被?ST说明连续三年出现财务亏损或经营不善等财务状况恶化现象,被ST说明连续两年出现财务问题。
因此,3858个实证样本中有3773个样本为财务正常样本、85个样本为财务危机样本,财务正常记为0、财务危机记为1。采用分层抽样,分别从正常样本和危机样本中随机抽取10%的样本(包含378个财务正常样本、9个危机样本)作为测试集Test,剩余的3471个样本(包含3395个财务正常样本、76个危机样本)作为训练集Train。
2. 预警指标的海选。本研究借鉴穆迪、中诚信等国内外评级机构及文献中的高频指标,从企业财务运营和经营环境两个层面来构建指标体系,如表1所示。
3. 决策树集成。本研究中3471个训练样本包含3395个财务正常样本(记为集合D)和76个危机样本(记为集合F),两类样本的比例约为45∶1,两类样本的数量极其不平衡。
对应前文所述的步骤,构建决策树集成的财务预警模型:
Step1:聚类。采用K均值聚类的方法,将训练样本中的财务正常样本集合D分为四类{D1,D2,D3,D4},样本个数分别为1633、1403、90、269。
Step2:生成多个训练样本。将Step1中划分的四类样本{D1,D2,D3,D4},分别与财务危机样本集F进行两两配对,形成了4个训练子集{D1∪ F,D2∪ F,D3∪ F,D4∪ F},4个训练子集中两类样本的比例分别为21∶1、18∶1、1.2∶1和3.5∶1。相比整体训练样本中两类样本的比例45∶1,训练子集中非平衡样本问题被大大削弱了。
Step3:决策树基学习器。利用前文所述方法,分别针对4个训练子集{D1∪ F,D2∪ F,D3∪ F,D4∪ F},利用决策树C5.0算法训练模型,并在置信度CF=0.75的设置下对决策树进行剪枝,从而训练出4个决策树基学习器{M1,M2,M3,M4}。此处以第一个训练子集训练出的决策树基学习器M1为例进行展示,见图2。
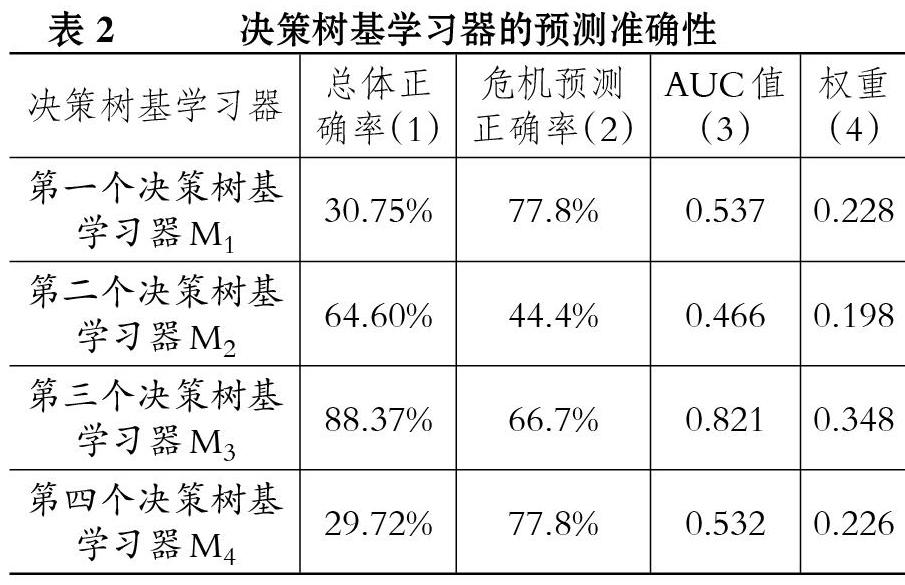
Step4:决策树集成。将四个决策树基学习器{M1,M2,M3,M4}在测试集Test上进行危机预测,分别计算四个决策树基学习器的预测总体正确率、财务危机的预测正确率(将实际危机样本预测正确的比率)。并根据画出每个决策树基学习器的ROC曲线,计算ROC曲线下方面积,即AUC值,如表2所示。以AUC值为权重对四个决策树基学习器进行集成,得到决策树集成学习器,即为最终的财务预警模型。
在测试集上进行财务危机预警的检验,预警的精度指标如表3第二行所示。基于决策树集成的财务预警模型对于测试集整体的预测正确率达到78.3%,财务危机的预测正确率达到77.8%。与表2中的基学习器相比,决策树学习器预警模型在总体正确率较高的基础上,大大提高了财务危机企业的正确识别率,兼顾了总体样本的预测正确率和财务危机样本的预测正确率,说明决策树基学习器的集成是有效的。
4. 对比分析。本研究采用“聚类Bagging”方法构建决策树集成模型,目的是解决财务危机样本过少情况下对于危机样本的预测准确度过低的问题。因此,将本研究构建的决策树集成模型与普通的决策树模型进行对比分析。对比模型是将全部训练样本直接构建一个决策树模型,再对训练集进行预警精度的检测,决策树中其他参数的设置均与本模型相同。将本模型与对比模型在测试集上的预警精度进行对比,结果如表3所示。
由表3可以看出,对比模型对于财务危机的预警几乎失效,近80%的危机企业都没有被识别出来,没有达到财务预警的根本目的。相较对比模型,本模型在财务危机样本的预测正确率上提高了55.6%,能够将绝大多数的危机企业正确预测出来,且能够使得总体样本的预测正确率达到78%以上的较高水平。这说明本预警模型在总体预测正确率较高的前提下大大提高了财务危机的正确识别率,更为合理。
四、結论
本文考虑了债券发行人中财务危机企业数量远小于财务健康企业的这种非平衡数据特征,借鉴“聚类Bagging”集成方法,通过K均值聚类的方法,将样本数量较多的财务健康企业样本分成K组,将K组财务健康样本与财务危机样本进行两两配对,形成K个大致平衡且有差异性的训练子集。利用决策树C5.0算法,在K个训练子集上分别构建决策树模型作为基学习器,使得决策树基学习器可以大致同等地学习健康样本与危机样本的特征,避免由于非平衡数据导致预警模型对数量较少的危机样本预测精度过低的问题。利用基学习器在测试集上的预测精度AUC值作为权重,对决策树基学习器进行加权,得到决策树集成模型,作为最终的财务预警模型,这使得预测精度高的基学习器在决策树集成模型中发挥更大的作用,提高了集成模型的预警精度。
经过测试集检验和对比分析,本文建立的基于决策树集成的财务预警模型精度较高,总体的预警正确率达到78%,对财务危机企业的正确识别率达到77.8%。而简单的决策树模型对于财务危机的预警几乎失效,近80%的危机企业都没有被识别出来,说明本模型能够在总体预警正确率较高的前提下大大提高财务危机的正确识别率。
【 主 要 参 考 文 献 】
[ 1 ] 杨贵军,周亚梦,孙玲莉.基于Benford-Logistic模型的企业财务风险预警方法[ J].数量经济技术经济研究,2019(10):149 ~ 164.
[ 2 ] 张发明,王伟明,李小霜.TOPSIS-GRA法下的企业动态信用评价方法及其应用[ J].运筹与管理,2018(9):136 ~ 142.
[ 3 ] 周忆,张友棠.基于卡尔曼滤波的僵尸企业财务风险动态预警研究[ J].财会通讯,2019(23):110 ~ 114.
[ 4 ] Mizen P.,Tsoukas S.. Forecasting US bond default ratings allowing for previous and initial state dependence in an ordered probit model[ J].International Journal of Forecasting,2012(1):273 ~ 287.
[ 5 ] 蔡立新,李嘉欢.大数据时代企业财务风险预警机制与路径探究[ J].财会月刊,2018(15):40 ~ 45.
[ 6 ] 李茜,唐恒书.基于三种BP-NNs改进算法的财务预警研究[ J].会计之友,2019(6):57 ~ 64.
[ 7 ] Sevim C., Oztekin A., Bali O., et al.. Developing an early warning system to predict currency crises[ J].European Journal of OperationalResearch,2014(3):1095 ~ 1104.
[ 8 ] 杨胜刚,朱琦,成程.个人信用评估组合模型的构建——基于决策树—神经网络的研究[ J].金融论坛,2013(2):57 ~ 61.
[ 9 ] 丁岚,骆品亮.基于Stacking集成策略的P2P网贷违约风险预警研究[ J].投资研究,2017(4):43 ~ 56.
[10] Javier De Andrés, Lorca P., Juez F. J. D. C., et al.. Bankruptcy forecasting: A hybrid approach using fuzzy c-means clustering and multi-variate adaptive regression splines (MARS)[ J].Expert Systems with Applications,2011(3):1866 ~ 1875.
[11] 庞素琳,巩吉璋.C5.0分类算法及在银行个人信用评级中的应用[ J].系统工程理论与实践,2009(12):94 ~ 104.
[12] 王茂光,葛蕾蕾,赵江平.基于C5.0算法的小额网贷平台的风险监控研究[ J].中国管理科学,2016(S1):356 ~ 363.

