对一道斜率比为定值试题的拓展探究
福建省仙游第一中学
一 试题及已有结论呈现
题目(2018年全国高中数学联赛重庆赛区预赛第9题)设椭圆C的左、右顶点为A(-a,0),B(a,0)过右焦点F(1,0)作非水平直线l与椭圆C交于P,Q两点,记直线AP,BQ的斜率分别为k1,k2,试证明为定值,并求此定值(用含a的函数表示).为定值文[1]把本题的结论推广到一般的圆锥曲线中,文[2]又把文[1]的结论由焦点F推广为定点M(m,0),得到了结论1、2、3,读后颇受启发,但觉意犹未尽,经探究发现,文[2]的结论1、2 可以拓展到更一般的情形.先把文[2]的结论1、2 抄录如下:
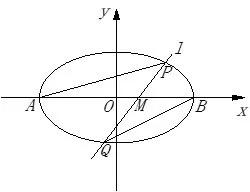
图1
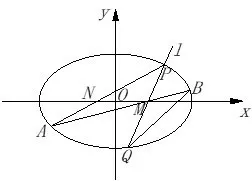
图2
结论1[2]设A,B为椭圆的左、右顶点,过点M(m,0)作任一条非水平直线l与椭圆C交于P,Q两点,记直线AP,BQ的斜率分别为k1,k2,则(如图1)
结论2[2]设A,B为双曲线0)的左、右顶点,过点M(m,0)作任一条非水平直线l与双曲线C交于P,Q两点,记直线AP,BQ的斜率分别为k1,k2,则
二 纵向拓展:由椭圆(双曲线)长(实)轴端点到定点弦端点的拓展
上述结论1、2 揭示了椭圆(双曲线)的左、右顶点,即长(实)轴端点A,B与过定点M(m,0)的弦的端点P,Q连线的斜率比为定值的性质,如果把长(实)轴AB这条过定点M(m,0)的特殊(过曲线中心)的弦拓展为过定点M(m,0)的一般的弦AB(异于PQ),直线AP,BQ的斜率k1,k2存在且非零,那么,是否为某个定值? 经探究,结论1 可拓展为
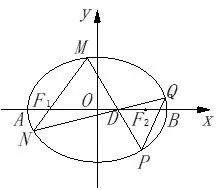
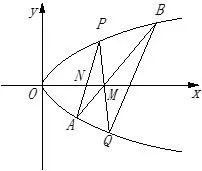
结论Ⅰ设椭圆的弦AB过定点M(m,0)(0< |m| < a).过定点M作非水平直线l与椭圆C交于P,Q两点,若直线AP与x轴交于定点N(n,0)(n 证明如图2,对于椭圆设定点M(m,0)(0< |m| < a),直线AP与x轴交于点N(n,0)(n < m),记直线AP,AM,PM的方程分别为x=h1y+n,x=h2y+m,x=h3y+m,把直线AP的方程x=h1y+n与椭圆C的方程联立,得b2(h1y+n)2+a2y2-a2b2=0,整理得 设A(x1,y1),B(x2,y2),P(x3,y3),Q(x4,y4),据韦达定理,得则同理可得 于是有 本题的答案是: 代入(2)式,得 又 推论设椭圆的弦AB过定点M(m,0)(-c < m < a,m ̸= 0),过定点M作非水平直线l与椭圆C交于P,Q两点,若直线AP与x轴交于左焦点(-c,0),直线AP,BQ的斜率k1,k2存在且非零,则为定值 在以上证明中,以“-b2”替换“b2”,可把文[2]的结论2拓展为 结论ⅠⅠ设双曲线C:的弦AB过定点M(m,0)(|m| > a),过定点M作非水平直线l与双曲线C交于P,Q两点,若直线AP与x轴交于定点N(n,0)(n 推论设双曲线的弦AB过定点M(m,0)(-c 特别地,当n=-a即点A,N(n,0)重合于左顶点(-a,0)时,由AB过点M(m,0)得点B为右顶点(a,0),且,结论Ⅰ、ⅠⅠ分别为文[2]的结论1、2. 例1 (2018年武汉大学自主招生试题)如图3,在平面直角坐标系xOy中,已知点F1,F2为椭圆1(a > b >0)的左、右焦点,A、B分别是椭圆C的左、右顶点,D(1,0)为线段OF2的中点,且 (1)求椭圆C的方程(答案: (2)若M为椭圆C上的动点(异于A,B),连接MF1并延长交椭圆C于点N,连接MD,ND并分别延长交椭圆C于点P,Q,设直线MN,PQ的斜率分别为k1,k2,试问是否存在常数λ,使得k1+λk2=0 恒成立? 若存在,求出λ的值;若不存在,说明理由. 图3 图4 结论Ⅰ、Ⅱ揭示了椭圆、双曲线过同一定点M的两条相交弦端点连线斜率比为定值的性质,那么抛物线是否具有类似性质? 如图4,对于抛物线C:y2=2px(p >0),设弦AB过定点M(m,0)(m >0),过点M作非水平直线l与抛物线C交于P,Q两点,若直线AP与x轴交于定点N(n,0),直线AP,BQ的斜率k1,k2存在且非零,那么是否为某个定值? 经探究可得抛物线的类似性质. 结论ⅠⅠⅠ设抛物线C:y2=2px(p >0)的弦AB过定点M(m,0)(m>0),过点M作非水平直线l与抛物线C交于P,Q两点,若直线AP与x轴交于定点N(n,0)(n < m),直线AP,BQ的斜率k1,k2存在且非零,则为定值 证明设直线AP,AM,PM的方程分别为x=h1y+n,x=h2y+m,x=h3y+m.把直线AP的方程x=h1y+n与抛物线方程y2=2px联立,得y2=2p(h1y+n),整理得y2-2ph1y-2pn=0. 设A(x1,y1),B(x2,y2),P(x3,y3),Q(x4,y4),据韦达定理,得y1y3=-2pn. 同理可得y1y2=-2pm,y3y4=-2pm.则y2=则所以 圆的即为定值证毕. 图5 特别地,当n=p=2,m=4时,这就是2010年全国高中数学联赛四川省预赛试题第14题的答案: 例2(2010年全国高中数学联赛四川省预赛第14题)已知F为抛物线y2=4x的焦点,M点的坐标为(4,0),过点F作斜率为k1的直线与抛物线交于A,B两点,延长AM,BM交抛物线于C,D两点,直线CD的斜率为k2.(1)求的值;(2)略(如图5).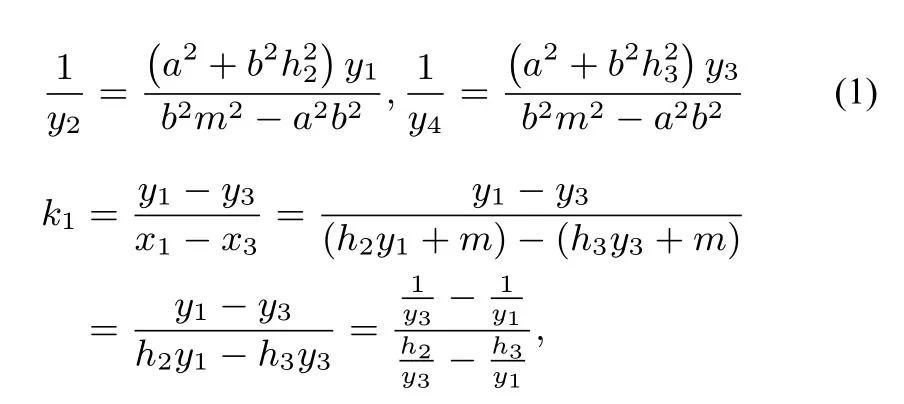
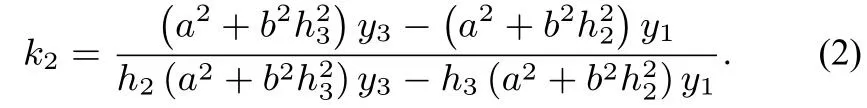
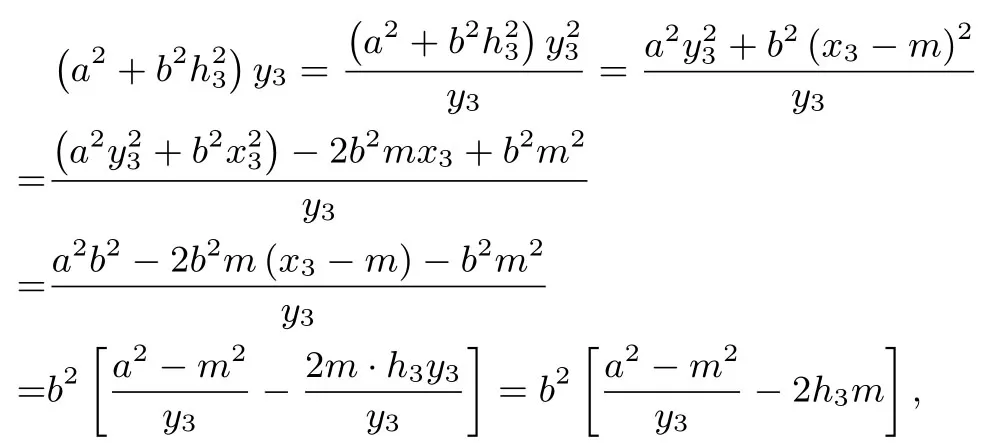
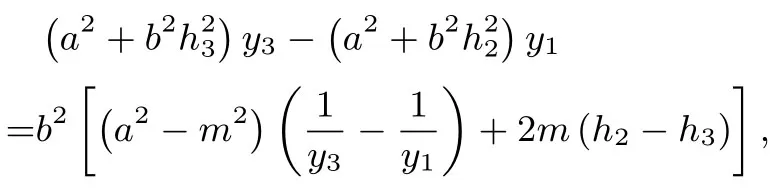
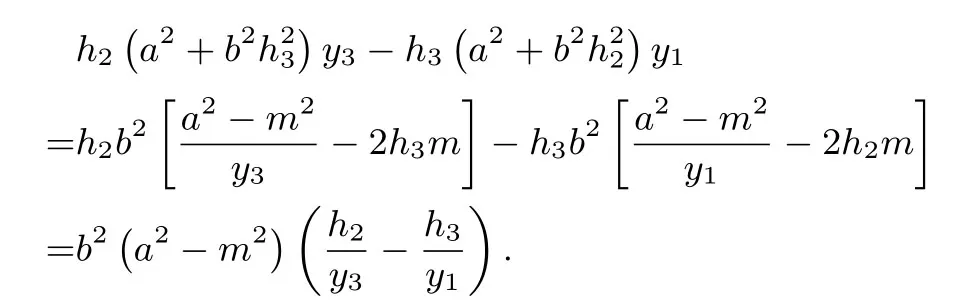
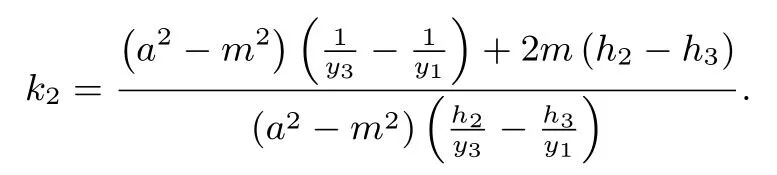
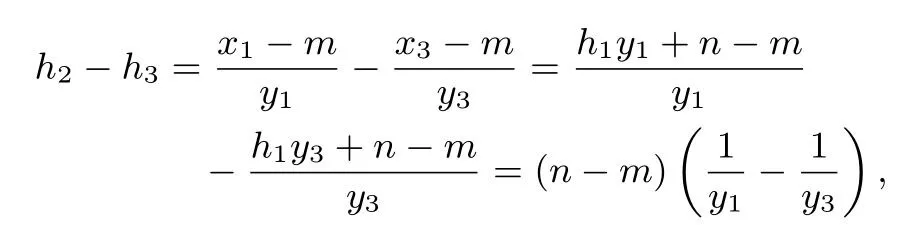
三 横向拓展:由椭圆、双曲线到抛物线的拓展