借助导数解决一道含参不等式试题*

北京市第十二中学高中部

近些年来,运用导数解决含参数不等式恒成立问题在各类考试中频繁出现,成为了新的热点.下面通过一道试题的解答,梳理这类问题的破解策略,供大家参考.

1 试题

题目(2018年1月北京市大兴区高三期末)已知函数

(1)求f(x)的单调区间和极值;

(2)若对于任意的x ∈[1,+∞),都有f(x)≤k(x2-1),求实数k的取值范围.

试题考查了导数公式、求导法则、导数在函数的单调性、极值问题中的应用以及含参数不等式恒成立问题,考查了学生的直观想象、数学运算、逻辑推理等核心素养.试题平中见奇,解法多样,给不同学生搭建了施展才能的舞台,下面重点谈一下第(2)问的解法.

2 解法探究

解法1(直接作差构造函数)

当x ≥1 时,xlnx ≥0,x2-1≥0, 所以k >0.设g(x)=k(x2-1)- xlnx, 则g′(x)= 2kx -lnx -1,

当k ≥时, 因为x ≥1, 所以2kx -1≥0,即g′′(x)≥0, 所以g′(x)在[1,+∞)上单调递增, 于是g′(x)≥g′(1)= 2k -1≥0, 所以g(x)在[1,+∞)上单调递增,于是g(x)≥g(1)=0,故k ≥符合题意.

综上,k的取值范围是

点评解法首先根据已知条件判断出k >0,这是不等式成立的必要条件,从而减少了后面讨论的情况,简化了运算.接下来作差构造函数g(x)=k(x2-1)-xlnx,并二次求导得到了然后怎样划分讨论的标准呢?由x ≥1, 得2kx ≥2k, 因此需要判断2k-1 与0 的大小,即分为与两种情况进行讨论.在说明不符合题意时, 借助函数的单调性构造了区间由此得到g(x)< g(1)= 0,从而说明该种情况不成立,体现了构造与分类讨论的思想方法.

变式1(2019年1月北京市昌平区高三期末考试)已知函数f(x)=lnx-ax2+2ax.

(1)若a=-1,求曲线y=f(x)在点(1,f(1))处的切线方程;

(2)若f(x)≤x恒成立,求实数a的取值范围.

解(1)略,y=x-2.

(2)设g(x)=f(x)-x=lnx-ax2+(2a-1)x(x>0),则

当a ≥0时,由x >0,得2ax+1>0,令g′(x)>0,得01.所以g(x)在(0,1)上单调递增,在(1,+∞)上单调递减,于是g(x)max=g(1)=a-1,令a-1≤0,得0≤a ≤1,故0≤a ≤1 满足题(意.)

当a <0时,存在满足g所以g(x)<0 不能恒成立,即a <0 不满足题意.综上,实数a的取值范围是[0,1].

解法2(先分离出lnx,再作差构(造函数).)当x ≥1时,xlnx ≤k(x2-1)等价于由x ≥1,得所以k >0.设则当k >0 且即时,g′(x)≥0,所以g(x)在[1,+∞)上单调递增,于是g(x)≥g(1)= 0,所以符合题意.当k >0 且Δ=1-4k2>0,即时,令g′(x)= 0,得或当时,因为g′(x)<0,所以g(x)在上单调递减,所以g(x)< g(1)= 0,这与x ∈[1,+∞),g(x)≥0 矛盾,所以不符合题意.综上,k的取值范围是

点评(解法)2 先将不等式xlnx ≤k(x2-1)转化为lnx ≤k然后再作差构造函数,这样做的优点是一次求导就可以达到解决问题的目的,而在解法1 中,一次求导之后还判断不了g′(x)的符号,还需要二次求导,所以解法2 与解法1 相比简洁了很多.因此,在解决含有lnx的超越不等式问题时应先把lnx分离出来再进行构造.

变式2(2016年高考课标ⅠⅠ卷文科第20题)已知函数

(1)当a=4时,求曲线y=f(x)在(1,f(1))处的切线方程;

(2)若当x ∈(1,+∞)时,f(x)>0,求a的取值范围.

解(1)略.

(2)当x ∈(1,+∞)时,f(x)>0 等价于lnx-令则g′(x)=

当a ≤2时,因为x ∈(1,+∞),所以x2+2(1-a)x+1≥x2-2x+1>0,即g′(x)>0,于是g(x)在(1,+∞)上单调递增,由此得g(x)>g(1)=0.

当a>2时,令g′(x)=0,得由x2>1 和x1x2=1 知,x1<1,所以当x ∈(1,x2)时,g′(x)<0,于是g(x)在(1,x2)上单调递减,即g(x)2 不符合题意.综上,a的取值范围是(-∞,2].

解法3(参变分离法)当x=1时,f(x)=k(x2-1)=0,所以不等式f(x)≤ k(x2-1)成立.当x >1时,由xlnx ≤k(x2-1),得

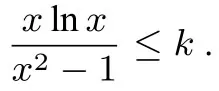
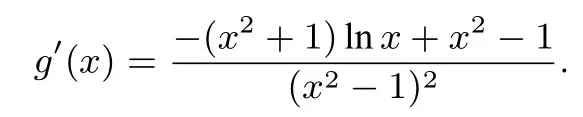
因为x >1,所以-2 lnx <0 且即h′′(x)<0,所以h′(x)在(1,+∞)上 单 调 递 减,于 是h′(x)< h′(1)= 0,所以h(x)在(1,+∞)上单调递减,于是h(x)< h(1)= 0,即g′(x)<0,由此得g(x)在(1,+∞)上单调递减.

点评参变分离法是解决含有参数不等式恒成立问题的常用方法,优点是将参数放在不等式一边,将不等式另一边构造函数,从而转化为函数的边界值与参数的大小进行比较,避免了讨论.本题在参变分离后求函数边界值时遇到了型,因而采取了洛必达法则,即

变式3(2016年全国高中数学联赛河北预赛)已知函数

(1)判断f(x)在定义域内的单调性;

(2)若f(x)<2x2在恒成立,求a的取值范围.

解(1)略.

(2)f(x)= lnx+在恒成立,即a <-xlnx+2x3.设g(x)=-xlnx+2x3,则g′(x)=-1-lnx+6x2.

设h(x)=g′(x)=-1-lnx+6x2,当时,故h(x)在上单调递增,所以

即g′(x)>0,所以g(x)在上单调递增,故g(x)>所以

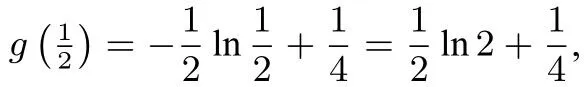
解法4(数形结合法)因为x ≥1,所以由xlnx ≤k(x2-1),得设则

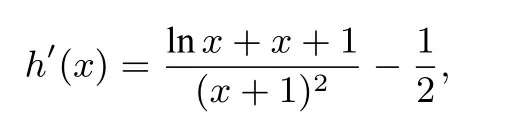
因为x ≥1,所以h′′(x)≤0,所以h′(x)在[1,+∞)上单调递减,于是h′(x)≤h′(1)= 0,由此得h(x)在[1,+∞)上单调递减,于是h(x)≤h(1)=0,即

这说明,曲线y=g(x)与直线相切于点(1,0),且在直线下方.由切线的定义以及斜率的几何意义知,当且仅当时,曲线y=g(x)在直线y=k(x-1)的下方,即x ≥1时,故k的取值范围是

点评数形结合法就是先把已知不等式变形,得到H(x)≥h(x),其中H(x)或h(x)为一次函数,然后分析直线和曲线的位置关系,找出直线和曲线相切时参数的值,在此基础上再借助切线的定义以及斜率的几何意义得出参数的范围.

变式4(2017年高考新课标Ⅱ卷文科第21题)设函数

(1)讨论f(x)的单调性;

(2)当x ≥0时,f(x)≤ax+1,求a的取值范围.

解(1)略.(2)由f′(x)= (-x2-2x+1)ex知,f′(0)= 1,且f(0)= 1,所以曲线y=f(x)在点(0,1)处的切线方程为y=x+1.

设g(x)=f(x)-(x+1)= (1-x2)ex-(x+1),则g′(x)=(-x2-2x+1)ex-1,所以g′′(x)=-(x2+4x+1)ex.因为x ≥0,所以g′′(x)<0,所以g′(x)在[0,+∞)上单调递减,于是g′(x)≤g′(0)= 0,由此得g(x)在[0,+∞)上单调递减,于是g(x)≤g(0)=0,即f(x)≤x+1.

这说明,曲线y=f(x)与直线y=x+1 相切于点(0,1),且在直线下方.由切线的定义以及斜率的几何意义知,当且仅当a ≥1时,曲线y=f(x)在直线y=ax+1的下方,即x ≥0时,f(x)≤ax+1,故a的取值范围是[1,+∞).

解法5(先必要条件后充分条件)由已知,得k(x2-1)-xlnx ≥0(x ∈[1,+∞))恒成立,设g(x)=k(x2-1)-xlnx,则g′(x)= 2kx-lnx-1,g(1)= 0.因为g(x)≥0(x ∈[1,+∞))恒成立,所以必有g′(1)≥0,即2k-1≥0,故

设h(x)=2kx-lnx-1,则当时,因为x ≥1,所以2kx-1≥0,即h′(x)≥0,故g′(x)在[1,+∞)上单调递增,所以g′(x)≥g′(1)=2k-1≥0(x ∈[1,+∞)),由此得g(x)在[1,+∞)上单调递增,所以g(x)≥g(1)=0.综上,k的取值范围是

点评解法5 根据x ∈[1,+∞)时,g(x)≥0,且g(1)= 0,得到了g′(1)≥0,即这是不等式成立的必要条件.

变式5(2015年高考北京卷理科第18题)已知函数

(1)求曲线y=f(x)在点(0,f(0))处的切线方程;

(2)求证:当x ∈(0,1)时,

(3)设实数k使得对x ∈(0,1)恒成立,求k的最大值.

解(1)y=2x;(2)略;(3)设

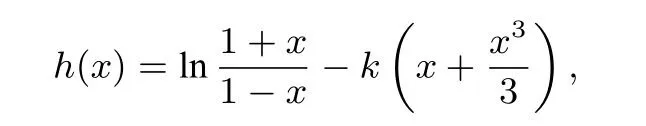
则

因为当x ∈(0,1)时,h(x)>0,且h(0)= 0,所以必有h′(0)= 2-k ≥0,即k ≤2.下面证明当k ≤2时,恒有h(x)>0.