捷联惯导动态粗对准受载体机动影响分析*

刘振亚，李永涛，常 岗

(中国华阴兵器试验中心，陕西华阴 714200)

0 引言

捷联惯性导航系统在定位工作前必须要进行初始对准，初始对准的好坏将直接影响到系统的导航精度[1-3]。从20世纪60年代开始，国内外专家学者开始对惯性导航系统(inertial navigation system， INS)初始对准理论与技术进行研究，在惯性导航系统误差模型、分段线性定常系统可观测理论以及大方位失准角情形下的捷联惯导初始对准方法等理论技术方面都取得了较大成果[4-6]。奔粤阳等提出了一种利用GPS辅助舰船捷联惯导系统实现行进间粗对准的方法[7]；ZHANG等针对运动条件下初始对准不确定性，提出改进容积卡尔曼滤波算法，达到了更高的对准精度及更强的数值稳定性[8]；XU等提出双模型对准算法，利用捷联惯性导航系统(SINS)两个计算回路实现快速准确的运动对准[9]。

目前，捷联惯性导航动态粗对准相关技术已较为成熟，各种算法也层出不穷，其主要目的都是为了提高对准精度[10-12]，而载体机动对对准精度的影响分析却缺少相应的研究。此外，动态对准技术的工程应用还处于起步阶段，尤其是陆用惯性导航装备相关测试方法还不够完善，不能针对对准原理对装备进行全面深入的考核，导致测试结果不全面、置信度不高。因此，急需研究试验过程中载体机动方式对捷联惯性导航装备初始对准性能的影响，从而设置载体机动考核路径与试验方法。文中基于经典的里程计辅助动态粗对准技术[13]，分析载体机动条件对SINS初始粗对准精度的影响，为制定有效可靠的陆用惯性导航装备动态对准测试方法提供理论支撑。

1 里程计辅助动态粗对准技术

载体在运动过程中，INS加速度计测量得到的加速度含有重力加速度、载体运动加速度及载体运动产生的科氏加速度，陀螺仪测量得到的角速度含有地球自转角速度及载体运动角速度。因此，传统双矢量定姿算法[14]得到坐标转换矩阵的静态粗对准方法已不能适用于动态对准。需要利用里程计信息重新构建矢量参考组，得到运动载体的坐标转换矩阵。各相关坐标系、欧拉角及其转换矩阵定义可参照文献[15]。

(1)

(2)

其中：ωie为地球自转角速度；φt为载体所在纬度值；Δλt=λt-λ0表示t时刻经度相对变化量。

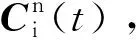
(3)

(4)

已知捷联惯性导航比力方程：

(5)

(6)

将式(6)代入比力方程式(5)，并向ib0系投影，最终得到：

(7)

(8)

式中，ui(t)及rib0(t)分别为式(7)两侧积分结果：

2 动态粗对准误差分析

根据上面推导过程，从误差源角度出发，对带有误差的坐标转换矩阵进行分类，并将坐标转换矩阵误差转化为相应的失准角，分析动态粗对准误差传播特性。

2.1 对准误差分类

2.2 误差传播特性

(10)

(11)

(12)

其中：φ×表示失准角的反对称矩阵。将式(3)代入式(1)，可得实际姿态矩阵表达式：

(13)

将式(10)～式(12)代入式(13)，忽略二阶误差化简可得：

(14)

(15)

其中，φi(ib0)表示失准角φib0在i0系中的投影。将式(15)代入式(14)，化简最终得到对准精度表达式：

φn=φn(ib0)+φn(i)

(16)

其中：φn(ib0)为失准角φib0在n系中的投影；φn(i)为失准角φi在n系中的投影。

3 粗对准精度受载体机动影响分析

在试验过程中，相比于精度已知的陀螺仪与加速度计，更关注载体的机动方式(即测试条件)对惯性导航系统动态粗对准精度的影响。因此，根据前文讨论的结果，从载体速度、加速度及角速度3种机动条件出发，分别对失准角φn(ib0)及φn(i)受载体机动的影响进行分析。

3.1 φn(ib0)影响因素分析

(17)

(18)

矢量形式表示为：

(19)

将φib0投影至导航系，并将式(19)两边积分可得:

(20)

(21)

3.2 φn(i)影响因素分析

(22)

由上式讨论可知，实际过程中rib0的表达式为：

(23)

(24)

(25)

根据矩阵2范数定义，可得：

(26)

(27)

(28)

(29)

由于陀螺仪在三轴方向的漂移误差基本相等，因此式(29)产生的误差项可忽略；只剩下式(28)产生的误差项，其大小与载体相对于惯性系角速度有关。为便于分析载体在导航系下机动对误差的影响，分析惯性系下的角速度：

(30)

(31)

结合式(31)，根据分析可知，动态粗对准精度与载体角运动相关，载体的水平转向角速度及俯仰角速度对对准精度有较大影响，且随里程计误差增大而扩大。

4 仿真分析

表1 车载惯导系统仿真初始条件

仿真结果如表2、表3、图1及图2所示。其中，θ、ψ、γ为车体姿态角，分别表示车体俯仰角、方位角和滚转角。根据结果可以看出，不同条件下各姿态角在初始时刻精度基本相同，并随着时间增长而逐渐变化。其中，俯仰角精度最高，其值保持在0.1 mil以内；滚转角精度次之，其值保持在0.2 mil以内；方位角误差最大，其最大值达到19.28 mil，远大于俯仰角及滚转角误差。因此，利用里程计辅助的SINS在粗对准阶段可以达到精度较高的水平对准，但其方位对准误差较大，需要进行精对准修正。

表2 车载惯导系统粗对准最大绝对误差 mil

表3 车载惯导系统粗对准均方根误差 mil

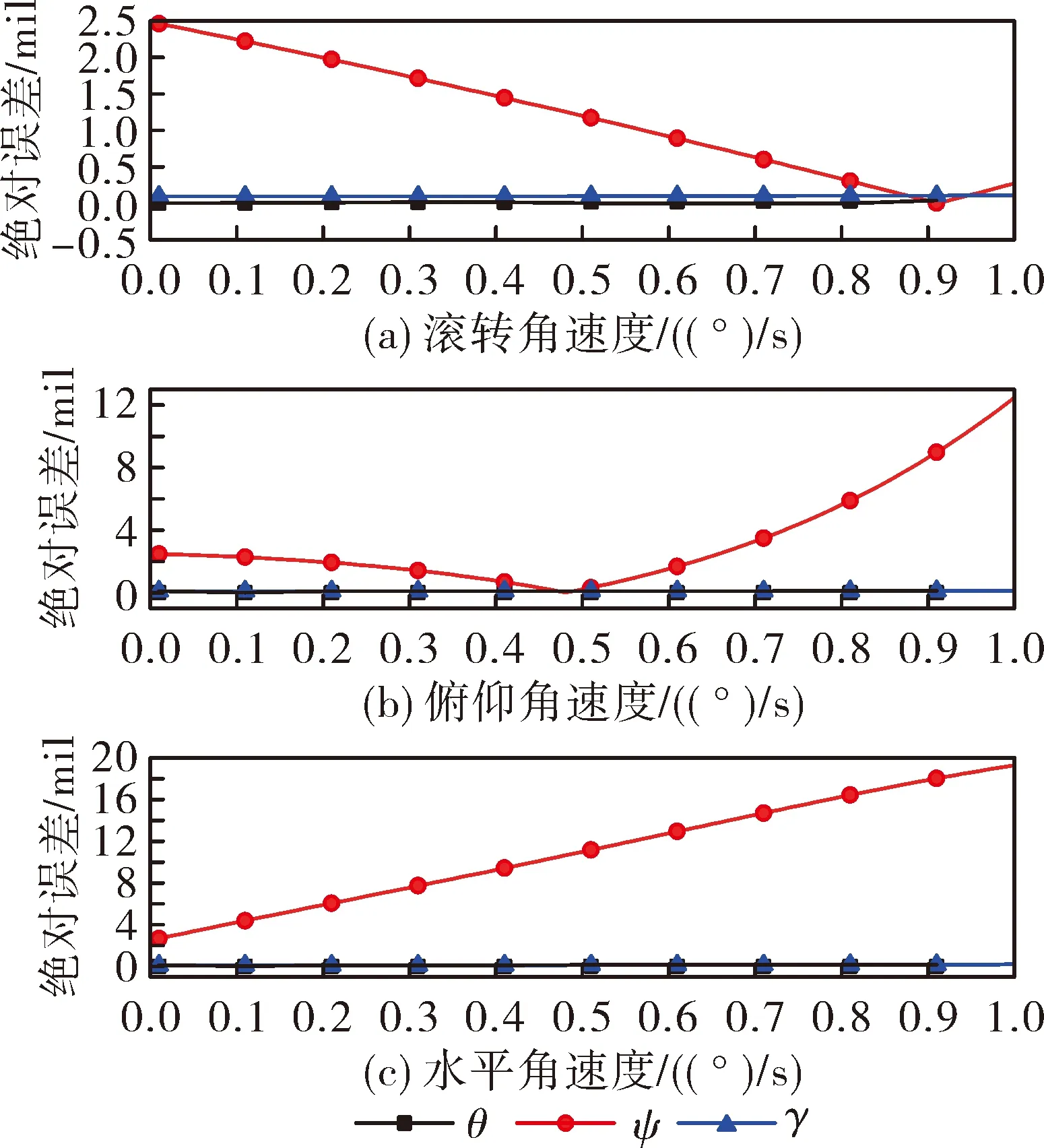
图1 不同角运动条件下粗对准绝对误差值

对比不同条件下惯导系统粗对准结果，车辆在不同速度及加速度直线运动过程中，各欧拉角均方根误差较小，其对准精度基本没有变化；车辆在不同角运动过程中，俯仰角及滚转角均方根误差较小，而方位角具有较大均方根误差。由表3及图1可知，车辆水平角运动及俯仰角运动对方位角对准精度有较大影响，而车辆滚转角运动对其精度影响较小。随着车辆水平角速度及俯仰角速度由0°/s增长至1°/s，方位角粗对准绝对误差值也随之剧烈上升，其均方根误差分别达到了4.96 mil、3.16 mil。此仿真结果与前文理论推导结果相一致。

图2 不同直线运动条件下粗对准绝对误差值

值得指出的是，车辆俯仰角速度变化时，前半段有误差减小的趋势是由于结果采取绝对误差表示造成的。其真实变化趋势为持续下降，恰好与车辆水平角运动误差变化趋势相反，再一次验证了式(31)的结果。

5 结论

1)利用里程计辅助捷联惯导系统进行动态粗对准过程中，其粗对准精度与载体直线运动及滚转运动基本无关，受载体水平角运动及俯仰角运动影响较大，且精度随着角速度的增大而降低。

2)在进行车载捷联惯导系统动态对准性能试验时，针对载体不同机动状态下动态粗对准精度的变化特点，可设置不同的运动路径及机动方式进行试验。从而得到装备性能边界，进一步摸清武器装备性能底数。

所得结论为车载捷联惯导系统动态对准测试方法提供了理论参考。