临近空间无动力攻击器弹道优化设计研究*
王莹莹,王 坚,岳韶华,何 苹
(1 空军工程大学防空反导学院,西安 710046; 2 西京学院信息工程学院,西安 710123)
0 引言
利用临近空间平台的高度和速度优势,发射无动力攻击武器,打击空中高价值目标,是一种有前景的选择[1-7]。对临近空间无动力攻击器(以下简称临空攻击器)弹道进行优化设计,是获取攻击器良好战技性能的有效途径。
和航空制导炸弹类似,临空攻击器也仅依靠载机的发射高度和速度来打击目标。因此,可参考航空制导炸弹,对临空攻击器的弹道进行设计。工程上常用的航空制导炸弹弹道方案分为两个阶段:滑翔段和俯冲段。在滑翔段,制导炸弹按照最大升阻比对应的攻角滑翔飞行,在接近目标末端,采用比例导引的方式俯冲攻击目标[8]。文献[9-11]指出这只是一种经验设计弹道,并不是理论上的最优弹道,设计初段按最佳升阻比滑翔、末段采用有约束比例导引飞行的弹道模式,认为该弹道模式可使制导炸弹获得更远的射程和更强的目标毁伤能力。
另外,临空攻击器与航空制导炸弹又存在较大差异。如美军GBU-39小直径炸弹,投放高度≤12 km,投放速度≤1.6Ma,GBU-39从投放到命中目标都处于航空空间[12]。而临空攻击器发射高度30~50 km,发射速度3~6Ma,从发射到命中目标跨越临近空间和航空空间[6-7]。这些不同点使得临空攻击器与航空制导炸弹战技性能差异较大,并且弹道呈现出不同的特点。
因此,文中借鉴航空制导炸弹弹道优化设计经验,并结合临空攻击器具体特点,设计临空攻击器弹道方案,采用均匀试验设计、偏最小二乘法、基于惩罚函数的遗传算法等综合方法,对临空攻击器弹道优化设计问题进行求解。
1 弹道方案设计
临空攻击器从发射点到命中目标点有多条弹道。弹道优化设计就是从这些弹道中选一条理想弹道,使攻击器具有良好的气动升阻特性、制导控制效率和攻击路线,并使攻击器射程、平均速度、末速度、法向过载、弹着角等战技术性能参数满足作战需求。
临空攻击器飞行跨越临近空间和航空空间。对于攻击器发射高度在40~50 km范围的情况,查美国1976大气标准,表1为40~50 km高度大气相对密度,其中h为高度,ρ为对应高度大气密度,ρ0为海平面大气密度,ε=ρ/ρ0。

表1 40~50 km高度大气相对密度
由表1可知,40~50 km高度空域空气极其稀薄,在42 km高空,大气密度仅为海平面的2.4‰。临空攻击器在40~50 km高度空域飞行时,气动力控制效率很低。通过大量仿真计算对比,40 km高度以下,攻击器才具备气动控制效率。因此,需研究攻击器在40~50 km高度空域飞行时,采用何种飞行弹道更为合适,并确定下滑攻角α1、侧滑角β1的值。
从40 km高度开始,攻击器弹道方案规划为滑翔段和有角度约束比例导引段。
在滑翔段,使攻击器以攻角α2滑翔飞行,主要目的是最大限度增加射程,此段飞行结束高度为hm1。攻角α2不能过大,攻角大固然可以提高升力,但同时会产生过多的诱导阻力,对提高射程反而不利,而且攻角过大会导致攻击器系统不稳定,但α2太小又不能起到明显的增程效果。另外,单从射程上来讲,当攻击器发射初始条件给定时,hm1越小则射程越远,但hm1过小会使末制导控制段时间太短,满足不了末制导要求。因此,需明确α2和hm1的值。
在有角度约束比例导引段,为了增强攻击器的突防能力和毁伤目标能力,希望攻击器的末制导段越陡峭越好,即弹着角要尽可能大。
考虑到命中角约束,将期望命中角修正量引入比例导引规律,纵向带有末端姿态角约束的制导律为[10,13]:
(1)
式中:k为纵向视线角速度比例系数;k1为期望命中角修正比例系数;θF为期望弹着角,取90°。由于偏航平面内不需要进行角度约束,所以该平面内导引律形式不需要修正项。式(1)等号右边第二项,就是期望命中角修正量,显然其大小和当前视线角q、期望弹着角θF都有关系,所以只要k、k1选取的适当,就会使末端弹着角达到要求。
需要说明的是,发射高度在30~40 km之间的攻击器弹道优化方案规划为滑翔段和有角度约束比例导引段,与以上分析过程类似,不再单独分析。
2 弹道优化数学描述
通过以上弹道方案设计,可以使临空攻击器在射程、末速度、平均速度等战技性能指标满足作战需求的前提下,有更大的弹着角。其中需优化的变量包括:攻击器在40 km以上高度飞行时的飞行攻角α1、侧滑角β1,攻击器在40 km以下高度飞行滑翔段攻角α2、滑翔段飞行结束高度hm1,比例导引系数k以及期望命中角修正比例导引系数k1。攻击器弹道优化数学描述如下:
(2)
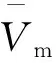
3 攻击器动力学方程
在常规弹道模型的基础上,综合考虑高空空气动力、重力加速度随高度与纬度的变化、地球曲率及自转等因素的影响,得到临空攻击器质心在发射坐标系下的动力学方程组为[6,14-15]:
(3)

4 仿真算例及分析
参考文献[4]和文献[7],表2为假定的发射参数。

表2 发射参数
4.1 攻击器在40 km以上高度飞行段弹道优化仿真
为了考察飞行攻角α1、侧滑角β1的值对攻击器弹道的影响,现假设如下仿真想定:攻击器从发射点飞行至40 km高度飞行段采用固定攻角α1、侧滑角β1飞行的方式,从40 km高度到命中目标采用标准比例导引弹道,目标在10 km高度以50 km为半径作巡航飞行。表3为仿真计算参数。
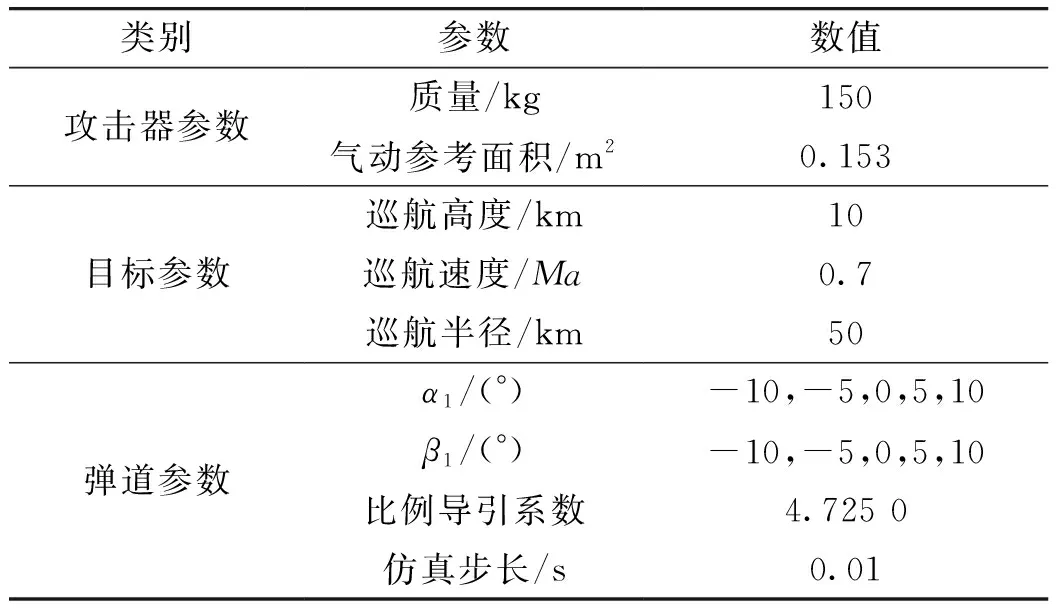
表3 仿真初始条件
当攻击器参数、发射条件、目标参数相同,α1分别取-10°、-5°、0°、5°、10°,β1分别取-10°、-5°、0°、5°、10°时,三自由度理想弹道仿真对比如图1所示。攻角随高度变化的对比如图2所示,侧滑角随高度变化的对比如图3所示,水平平面法向需用过载与可用气动过载的对比如图4所示,垂直平面法向需用过载与可用气动过载的对比如图5所示。
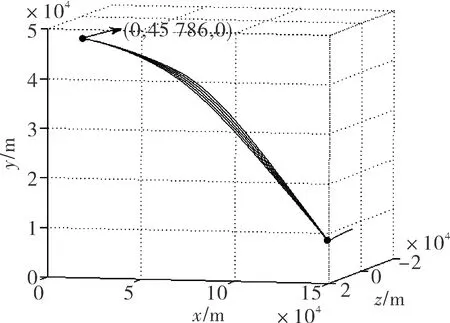
图1 不同α1、 β1对应的弹道对比
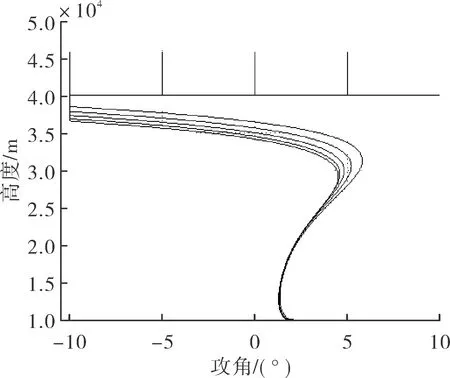
图2 不同α1、 β1对应的攻角变化对比
综合分析图1~图5可知,α1、β1分别取不同值时,对应攻击器全弹道、全弹道垂直平面法向过载、水平平面法向过载,以及在40 km以下高度,攻击器攻角、侧滑角均相差较小。因此可得以下结论:对于发射高度大于40 km的临空攻击器,在40~50 km高度空域飞行时,只要需用过载小于可用气动过载,下滑攻角α1、 下滑侧滑角β1可以在[-10°,10°]范围内任意取值,最节约能量的方式是α1=0°、β1=0°,攻击器采用惯性飞行的方式。

图3 不同α1、 β1对应的侧滑角变化对比
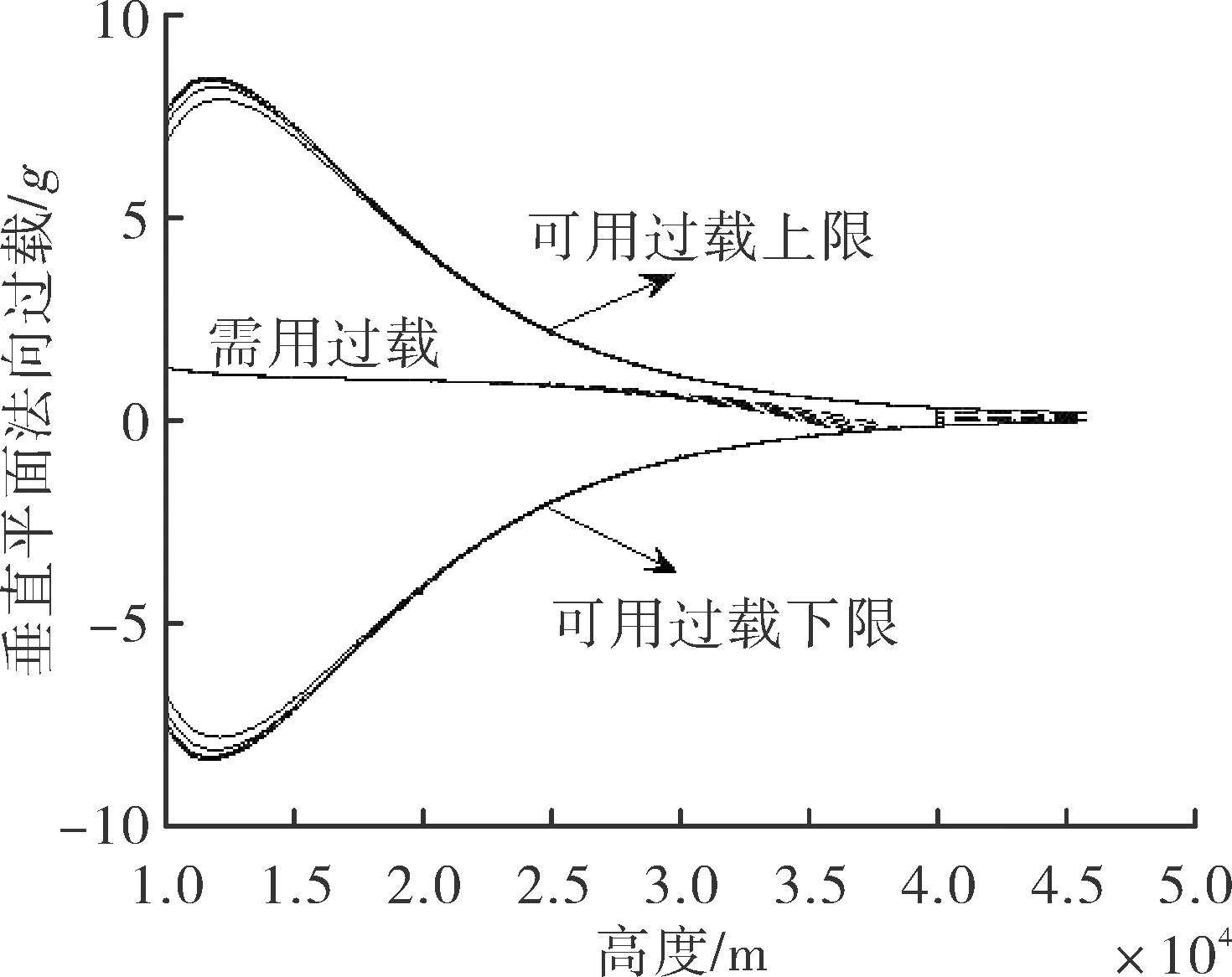
图4 不同α1、 β1对应的垂直平面法向过载对比

图5 不同α1、 β1对应的水平平面法向过载对比
4.2 攻击器在40 km以下高度飞行段弹道优化仿真
从40 km高度开始,攻击器以较大攻角α2滑翔飞行,此段飞行结束高度为hm1。从hm1高度开始,进入末制导阶段,末制导阶段纵向制导引入具有姿态角约束的比例导引律,对攻击器在40 km以下高度飞行段弹道优化设计进行仿真计算,计算流程如图6所示[3,7]。
通过优化计算,得到优化解:α2=7.763 4°,hm1=29.444 km,k=3.001 2,k1=0.022 0。
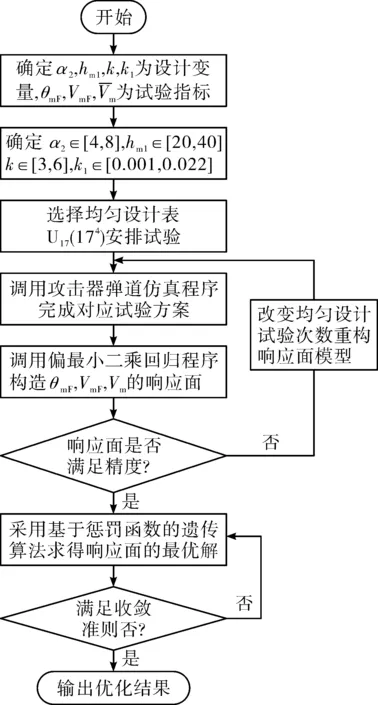
图6 弹道优化仿真计算流程图
综上分析,得到发射高度hf为45.786 km、发射速度VmF为1 829.2 m/s、发射弹道倾角θf为-3.560 8°、发射弹道偏角ψv为0°的临空攻击器弹道优化结果如图7所示。

图7 弹道优化设计结果示意图
图7中,攻击器从发射点到命中目标的优化弹道为:1)0~26.2 s时间段,攻击器飞行高度由发射高度45.786 km下降至40 km,采用惯性飞行方式,攻角0°,侧滑角0°。2)26.2~57 s时间段,攻击器飞行高度由40 km下降至28.7 km,垂直平面内,攻击器以7.763 4°攻角滑翔飞行;水平面内,按标准比例导引律飞行。3)57~93.3 s时间段,攻击器飞行高度由28.7 km高度降至目标巡航飞行高度10 km,垂直平面内,按有角度约束比例导引律飞行;水平面内,按标准比例导引律飞行。
临空攻击器弹道优化前后对比如图8所示。

图8 弹道对比图
优化后的弹道与优化前相比,前段弹道更为平缓,达到了滑翔增程的目的,后段飞行弹道更为陡峭,增强了攻击器的突防能力和目标毁伤能力。表4为弹道优化前后,临空攻击器飞行性能对比。

表4 弹道优化前后攻击器飞行性能比较
由表4可看出,弹道优化后攻击器末速度、平均速度有所提高,飞行时间有所缩短,且都满足作战需求,同时攻击器末端弹道倾角绝对值大幅增加,达到了弹道优化的目的。
5 结论
对临空攻击器弹道进行了优化设计,优化后的弹道分为三段:惯性飞行段、滑翔增程段、有角度约束比例导引段。攻击器发射高度在40~50 km范围时,攻击器飞行高度在40 km以上飞行段,采用惯性飞行弹道,攻击器最省能量、平稳飞行的方式是飞行攻角为0°、侧滑角为0°;攻击器飞行高度在40 km以下飞行段,采用滑翔和有约束比例导引飞行弹道,可以达到既增加射程,又保证更大的弹着角命中目标的目的。研究结果对于临近空间装备发展具有一定牵引作用。

