渗透数形结合思想 发展数学核心素养

李淑艳

摘要：数形结合思想是一种重要的数学思想，数形结合法是一种重要的数学教学方法。如果长期渗透，运用恰当，则使学生形成良好的数学意识和数学思维能力，有效促进学生数学核心素养的形成与发展。

关键词：小学数学；数形结合；核心素养

中图分类号：G623.5文献标识码：A文章编号：1009-010X（2020）31-0033-03

核心素养理念下，“小学数学教学如何培养学生具备适应未来学习的数学学习能力、数学思维方式及必备品格”这一课题摆在每一位一线教师面前。小学生抽象思维能力较低，数形结合通过“数”与“形”的相互转化，能把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来解决问题，可以使复杂问题简单化，抽象问题具体化，能有效地帮助学生理解知识，优化解题途径，培养思维品质。

一、概念教学中“数形结合”，理解概念本质

小学生思维模式较为简单，以形象思维为主，而教材中数的认识、数的意义、数的性质等内容，都是比较抽象的概念，应用“数形结合”，通过用具体的实物或直观的图形来阐述数学概念，使抽象的概念具体化、形象化，能帮助学生理解概念，抓住本质。

例如，教学“万以内数的认识”时，计数单位“个、十、百、千”及它们之间的“十进制”关系是非常重要的概念，对学生数感的培养至关重要。这几个概念极为抽象，学生难于理解，怎么办？教学中采用数形结合的方法，用一个小正方体表示“一（个）”，把10个小正方体摞在一起表示“十”、把十个“十”即100個小正方体拼在一起就是“百”，把十个“百”即1000个小正方体放在一起就组成了“千”。如图1：

结合小立方体的变化，学生直观认识了计数单位“个”“十”“百”“千”，也理解了它们之间的“满十进一”的十进制关系。

二、计算教学中“数形结合”，发展计算素养

计算能力是小学生数学核心素养之一。计算教学绝不仅仅是让学生多做题、做对题，而是要引导学生通过自主探究，感知理解算理，灵活掌握方法，提高计算素养，培养数学思维。教学中通过“数形结合”，把算理算法寓于形象直观的图形中，可以丰富表象、引发联想、分类比较、提升能力。

如教学“异分母分数加减法”，为什么异分母分数加减法要先通分？利用数形结合可以使学生直观看到（图2）：因为分数单位不同，异分母分数不能直接相加减，只有转化成分母相同的分数，才能进行计算。同学们通过看图意识到“通分”的必要性，从而理解异分母分数加减法的算理：“只有分数单位相同的数才能相加减”。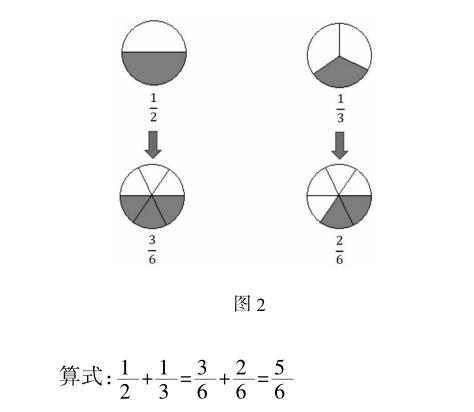

直观的演示，清晰表达了算理算法，此时教师没有就此止步，而是进一步深化：分数加减法和整数、小数加减法有什么关系？师生共同归纳：整数、小数、分数加减法虽然计算法则不同，整数加减法是“相同数位对齐”，小数加减法是“小数点对齐”，分数加减法“同分母分数相加减，分母不变，只把分子相加减”“异分母分数是先通分，再按同分母分数加减法的法则进行计算”。但“不同”背后却蕴藏着“相同”：都是“把相同单位的数进行相加或相减”，算理是相同的。至此学生构建了加减法计算的知识结构，形成了自己的知识体系。

三、问题解决时“数形结合”，提升解题能力

在解决问题时，尤其遇到较难理解的题目时，画图能充分地体现数形相结合的优势：直观地显示题意，有条理地表示数量，便于发现数量之间的关系，利于学生对问题的分析和理解，从而形成解题的思路。因此画图是帮助学生解决数学问题的重要方法，

如一年级思维拓展训练中的排队问题：10个小朋友排成一队做游戏，“从前往后数，小红在第5位，从后往前数小红在第几位？”

看到这样的题目，绝大多数同学都说小红从后往前数排在第5位。“是这样吗？你是怎么想的？”教师不急于评价，而是让10个学生到前边站成一排，小红站在从前数第五的位置，让学生们一起从后数看小红到底排第几？通过排一排，数一数的活动，学生直观的看到从后数小红排第6，也明白了“一共10个同学，从前数小红排第5，那么小红的后边还有5个同学，从后数到小红就是第六”的道理。问题解决了，今后再遇到排队的问题，怎样保证是正确的？指导学生们画图表示出来：

前数第五，后数第六

通过实际活动和画图，有效地突破了排队问题的难点，再告诉学生，遇到类似问题，先画画图，就能轻松的解决。就像我国著名数学家华罗庚说过的“数缺形时少直观，形少数时难入微，数形结合百般好，隔裂分家万事休”。

四、探索规律时“数形结合”，发展创新思维

学生的数学学习不仅仅是接受知识、积累知识的过程，还是一个探索知识，创造知识的过程。数形结合，有助于学生探索规律、发现规律，对发展学生的思维起到至关重要的作用。

综上所述，渗透运用好数形结合思想，能将抽象的数学概念具体化，能把无形的解题思路形象化，不仅有利于学生顺利、高效的学习，更有利于学生兴趣的培养、能力的提升、智慧的启迪。学生在学习中逐步养成“数形结合”习惯，形成“数形结合”思想，会促进他们数学核心素养的发展。