旋流微气泡气浮除油过程的数值模拟

贺彦涛， 王玉环， 蔺爱国， 李 娟

(1.中国石油大学(华东) 化学工程学院，山东 青岛266580；2.中国石油大学(华东) 科学技术研究院，山东 东营 257061)

目前针对有机物含量高、高悬浮物、高色度、高含盐的石油工业废水，常用物理分离法、化学法、物理化学法及生物法等方法处理，但是在处理过程中存在诸多缺点，如占地面积大、停留时间长、对管线或操作人员的腐蚀性以及某些物质的致癌性等[1-5]。气浮技术因处理效率高、投加化学药剂剂量少的特点而被广泛使用。国内外专家学者基于气浮技术研制出不同类型的气浮装置[6-10]。但是由于现有测量仪器的限制，无法对装置内部流体的速度变化及运动轨迹进行测定。随着计算机技术的发展，采用计算流体力学数值模拟的手段对其进行仿真成为可能。笔者利用商业软件ANSYS中的FLUENT组件对旋流微气泡气浮装置进行数值模拟，主要模拟油滴粒子的运动轨迹及内部流场，考察进口流量、微气泡粒径对装置的影响。

1 物理模型和边界条件

本研究针对的问题是油滴如何快速从水中除去，具体为油滴颗粒在絮凝剂、微气泡单一或共同作用下如何形成絮体并快速从水中去除的过程。该过程实际上也受到悬浮物颗粒的影响，因此，该过程数值模拟涉及气-液-固三相流问题。目前的数学模型仅可简单描述气-液或液-固两相流，即气泡-液体颗粒或者液体颗粒-固体颗粒，之间的相互作用，与实际过程仍有区别。在模拟气浮过程中引入固体颗粒后，增加了油滴颗粒的可变性及微气泡的碰撞聚并的不确定性，使得油滴、微气泡附着在固体颗粒表面的过程更加复杂。针对此类问题的模型仍处于开发阶段，尚不能投入实际使用[11-12]。故在进行数值模拟的过程中仅考虑微气泡的影响，即简化为气-液两相流问题。在对旋流微气泡气浮装置进行数值模拟时，为降低对计算机硬件的要求以及降低模拟的难度，在进行数值模拟时只对装置的内筒进行模拟。图1为旋流微气泡气浮装置内筒简化的结构示意图。以结构化六面体单元用ANSYS软件中的MESH组件对其进行网格划分，并对入口处的网格进行加密处理，划分后的网格示意图见图2。

结合实际工况，对模型混合物(油、水和空气的混合物)参数设置如下：空气气泡的ρair=1.225 kg/m3，μair=1.7894×10-5Pa·s，dair=3.0×10-5m；油滴的ρoil=860 kg/m3，μoil=0.048 Pa·s，doil=1.5×10-5m；进口混合物中油质量浓度设为600 mg/L，进口混合物流量为600 L/h，含空气体积分数10%。进口边界设置为速度入口，其进口速度由公式(1)决定。

(1)

气相和油相的进口速度与进口流体速度相同，进口的气相体积分数的设定依据实际情况。油相采用离散相模型，面源射流进入；油滴颗粒等效为直径15 μm的刚性球体颗粒；装置壁面碰壁条件设置为反弹，顶部出口碰壁条件设置为捕集，底部出口碰壁条件设置为逃逸。对模型的出口边界条件设置为出口流量边界条件，采用FLUENT软件默认参数，仅对出口的流量比例进行更改。壁面、底板等设置为无滑移壁面边界条件，其中各向速度为0。

本研究中采用多相流模型描述气-液两相流;采用离散相模型模拟粒子运动轨迹；利用RNGK-ε模型描述装置内部的湍流运动，并利用FLUENT 17.0软件进行求解。

2 数学模型选择

2.1 流体模型

针对旋流气浮装置，在进行CFD数值模拟时对气、液两相流的处理方法主要为Euler-Lagrange方法和Euler-Euler方法。Euler-Lagrange方法是将液体作为连续相，将油滴粒子作为离散相，通过Lagrange坐标下的运动轨迹模型来获取油滴粒子的运动轨迹，被称为离散相模型。Euler-Euler 方法是将液体和气体看作相互交融的连续介质，又被称为双流体模型。Euler-Lagrange模型假定液体对油滴粒子的运动会产生影响，但油滴粒子不影响液体流动，其好处是模型物理概念直观，可以给出油滴粒子运动的详细信息，缺点是不能完整地考虑油滴粒子在各种湍流中的运动轨迹且计算量太大。Euler-Euler 方法两相间的耦合是通过质量、动量和能量守恒方程之间的相互作用实现，各相的控制方程形式相差不大，对计算能力的要求比 Euler-Lagrange 方法低[13-15]。因此，在本研究中采用Euler-Euler方法即双流体模型对旋流微气泡气浮装置中的气、液两相流进行数值模拟；采用 Euler-Lagrange 离散相模型对油滴粒子的运动轨迹进行模拟。

2.2 湍流模型

湍流模型的选择也会对模拟结果产生影响。当旋流气浮装置内部流场为高强度湍流流动时，标准K-ε模型将不再适用，因此需对其进行修正或选用其他模型。RNGK-ε模型的基本思想认为湍流是受随机力驱动的输送过程，将其中的小尺度涡忽略但将其影响并到涡黏性中，以便得到所需要尺度上的输运方程，因此使得RNGK-ε模型更适应于具有旋转流动的流场计算。RNGK-ε模型考虑到流体旋转带来的影响，因此提高了高旋转流动模型的计算精度。RNGK-ε模型中的系数由理论公式计算得出而不是依靠经验来确定，因此其适应性更强[16-19]。

基于RNGK-ε模型理论，其湍动能K和紊动能耗散率ε的输运方程如式(2)～(6)所示。

K方程：

(2)

SK=G-ρε

(3)

(4)

ε方程：

(5)

(6)

方程中的经验常数为：C1=1.44，C2=1.92，σK=1.0，σε=1.3。

2.3 离散相模型

为获取油滴粒子的运动轨迹，通过Lagrange坐标下的运动轨迹模型以单个油滴粒子为计算对象进行模拟计算。单个油滴粒子平衡方程在Cartesian坐标系内的表达式如式(7)所示。

(7)

式(7)中，右边第一项为流体对颗粒的单位质量曳力，第二项为流体相的流动对油滴粒子的附加力，第三项为由于压力的变化而对油滴粒子产生的压力梯度力。其中，单位质量曳力表现形式如式(8)～(10)所示。

(8)

(9)

(10)

公式(9)中α1、α2、α3为常数。

3 计算结果及分析

3.1 粒子运动轨迹

定义模型的底部出口为y=0 mm平面，进口方向为由“-z”向“+z”方向自筒壁切向射流进入。图3 为旋流微气泡气浮装置内油滴粒子的运动轨迹图。从图3可以看出，油滴粒子在进入装置后做内外双螺旋运动，且迅速由外螺旋转至内螺旋向装置的中心部位做向心运动。油滴粒子在进入装置后在空腔段及大锥段的运动轨迹线十分密集，但在小锥段则变得很稀疏。可以认为，如果油滴粒子无法在空腔段和大锥段完成向心运动，并随与微气泡形成的絮体上浮至装置的顶部除去，则很容易随流体从底部逃逸。油滴粒子在外螺旋的速度远大于内螺旋的速度，与已有的模拟结果[20]相似。

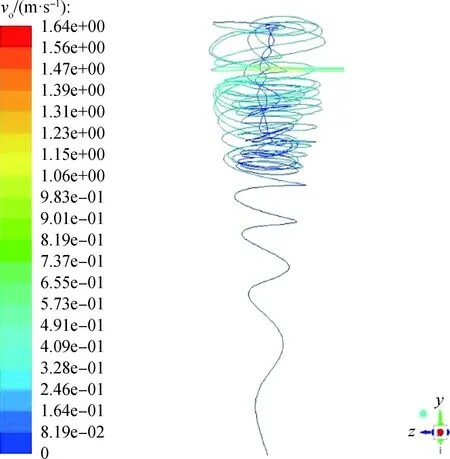
图3 旋流微气泡气浮装置内油滴粒子运动轨迹模拟图Fig.3 Simulation diagram of oil droplet particle motiontrajectory in a swirling microbubble air flotation device

3.2 内部流场速度分布

图4为利用FLUENT软件得到的流体速度径向分布图。图4(a)和图4(b)分别为模型混合物进口流量600 L/h时不同截面处的切向速度沿径向分布图和不同进口流量在高度900 mm截面处的切向速度沿径向分布图。由图4(a)和图4(b)可以发现，切向速度随着进口流量的增加而增大，在不同高度处的切向速度分布规律相似，但是其具体数值随着高度的降低而减小，其中流体的黏性以及与筒壁的作用力贡献最大，与已有研究[21-22]对照可知，当装置的长度或者高度达到一定数值时，必定会出现某截面处的切向速度为零的现象。

在实际工作中，径向速度的测定是非常困难的，即便使用最先进的激光测定技术也无法准确获得装置内部流体的径向速度分布。模型混合物进口流量为600 L/h时不同高度截面处的流体径向速度分布见图4(c)。可以看出，径向速度沿半径向装置中心处递减。

不同高度截面处流体的轴向速度沿径向分布见图4(d)。可以看出，轴向速度在装置中心部位两侧呈对称分布且有正负速度之分。装置在高度800、900及1050 mm截面处的轴向速度均存在着轴向速度为零的点；在高度400 mm截面处的轴向速度为负值。这说明在装置的内部不同高度截面处存在着一系列轴向速度为零的点，并形成了零速度面。轴向速度的大小影响油滴的去除效果，轴向速度太小会增加油滴在装置内部的停留时间，容易造成油滴粒子逃逸，去除效率降低。

结合对气浮装置中废水三维速度的模拟结果[21]分析可知，当微气泡-油滴絮体的切向速度和径向速度足够大，使其由负轴向速度区域越过零速度面进入正轴向速度区域，从而改变其轴向速度的大小和方向，使得具有正的轴向速度的微气泡-油滴絮体被快速带至装置顶部形成浮渣而被除去。但是当切向速度和径向速度太小时，不足以使得微气泡-油滴絮体越过零速度面；或者速度过大时，微气泡-油滴絮体越过零速度面进入正轴向速度区域后再次穿越过零速度面进入负轴向速度区域，则很容易随流体的流动从底部出口逃逸，造成模拟油-水分离的效果降低。

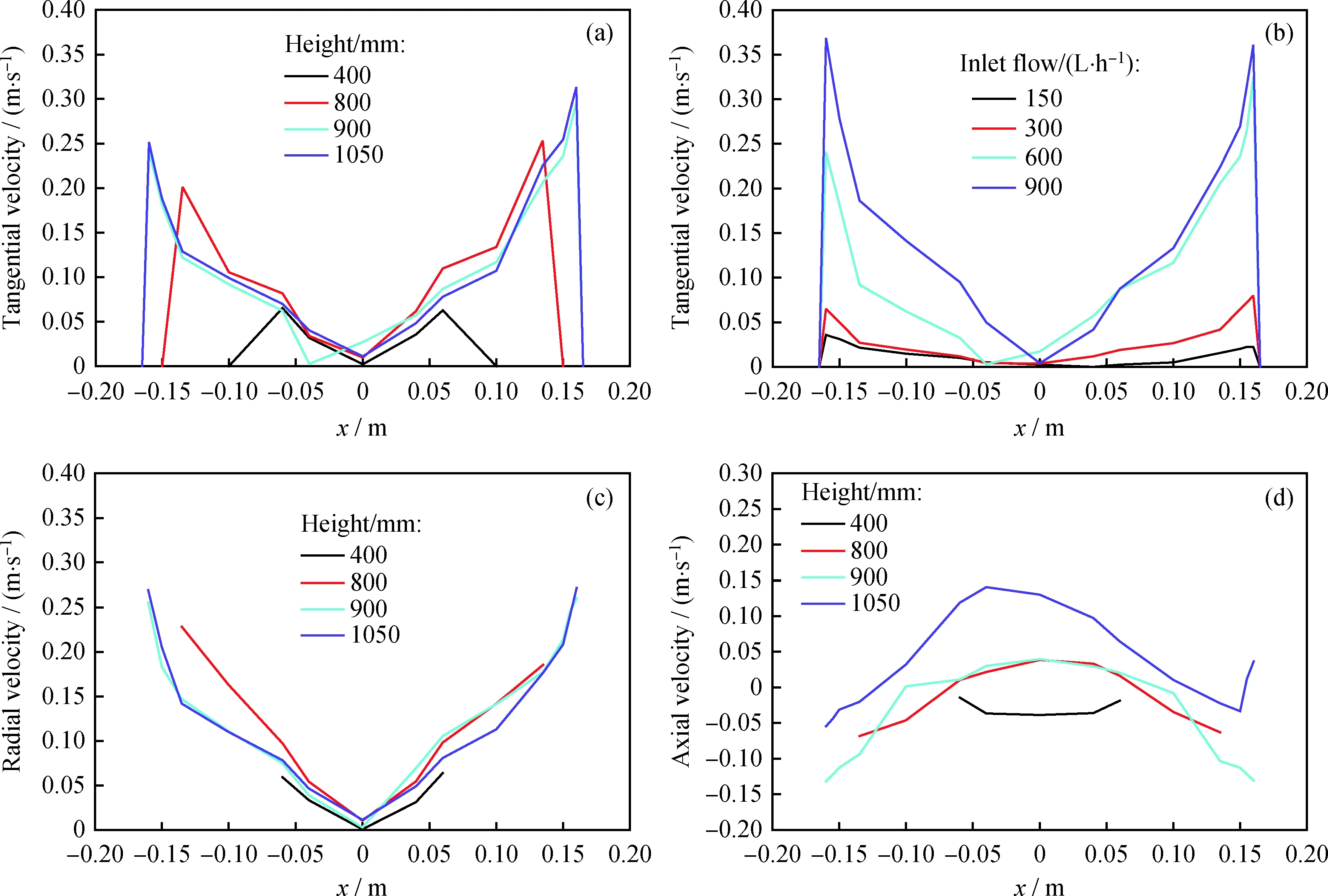
图4 不同混合物进口流量和不同装置高度对速度分布的影响Fig.4 Influence of different inlet flow rates and different heights on velocity distribution(a) Tangential velocity at different heights (inlet flow 600 L/h, with 10% volume fraction air);(b) Tangential velocity at different inlet flows (height 900 mm, with 10% volume fraction air);(c) Radial velocity at different heights (inlet flow 600 L/h, with 10% volume fraction air);(d) Axial velocity at different heights (inlet flow 600 L/h, with 10% volume fraction air)

3.3 气体对旋转流场的影响

微气泡在装置内部的分布状态是影响微气泡吸附、捕获油滴颗粒形成微气泡-油滴絮体的重要因素之一。图5为经FLUENT软件模拟所得到的平均气相体积分数随时间的分布图。由图5可见，在 98 s 后装置的整体平均气体分布系数达到初始设定值。图6为不同粒径气泡气相分布云图。由图6可见，随着气泡粒径的减小，气体在装置内的分布更为均匀。当气泡粒径为100 μm时，装置底部气相体积分数极小，意味着微气泡量极少，势必会降低气泡对油滴的捕获效率，不利于油污的去除。当气泡粒径为30 μm时，气相体积分数相对均匀，表明气泡在装置内部的分布比较均匀，更易捕获油滴形成微气泡-油滴絮体，提高去除效率。

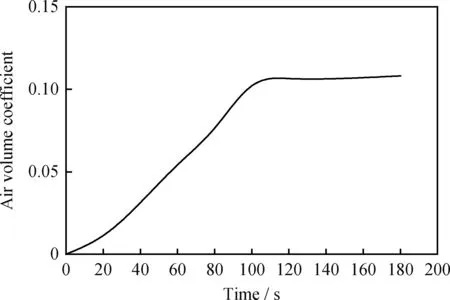
图5 平均气相体积分数随时间的分布Fig.5 Average gas phase volume coefficientdistribution over time

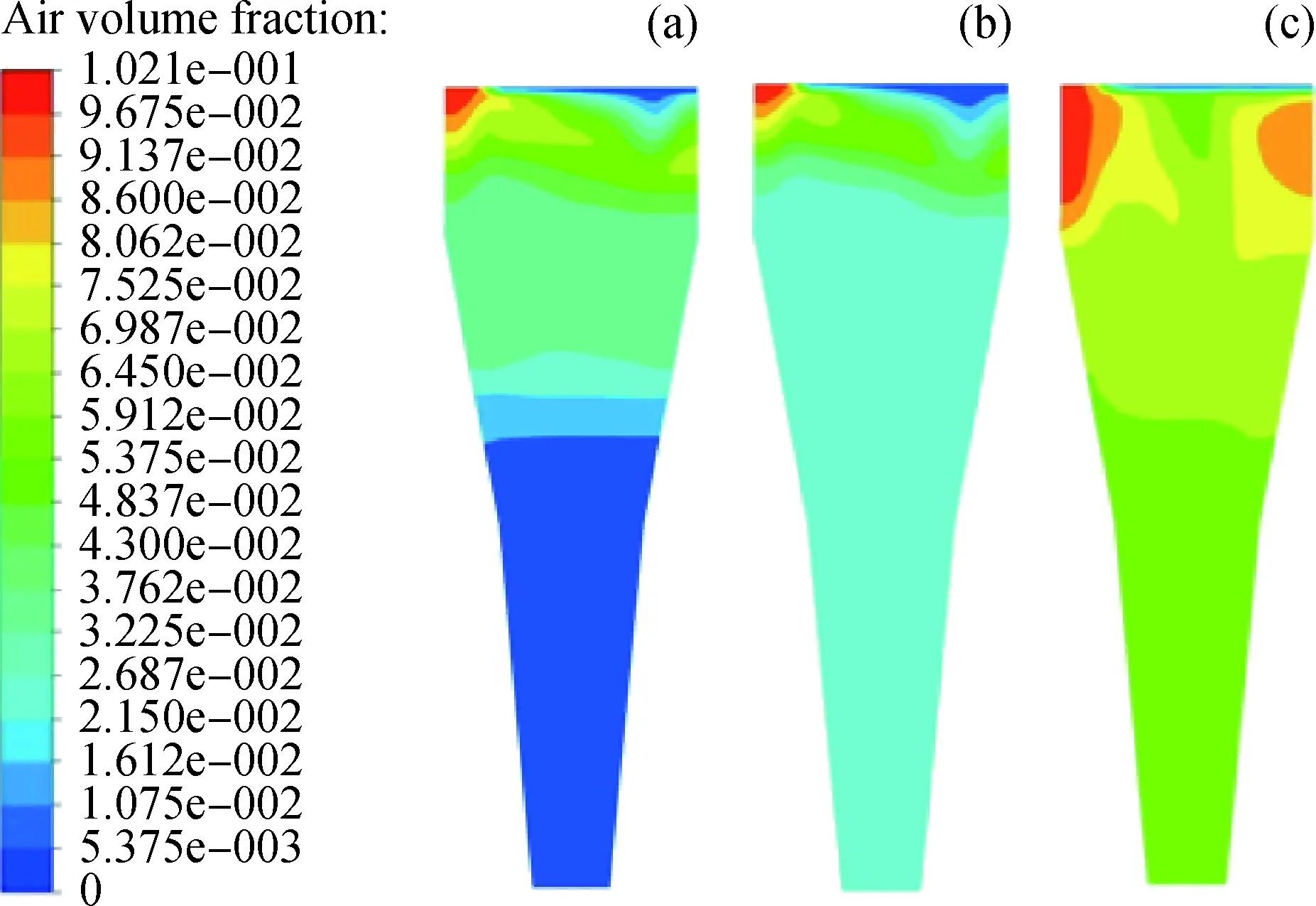
图6 不同粒径气泡气相分布图Fig.6 Gas phase distribution of different sizes of bubblesGas bubble size/μm: (a) 100; (b) 50; (c) 30

在只改变气体含量并保持其他参数设置不变情况下的切向速度和轴向速度对比见图7。可以看出，与通入气体时相比，不通入气体的情况下截面处的切向速度和轴向速度均有所降低。虽然切向速度的变化趋势相似，但是通入气体后切向速度的数值比未通入气体时数值更大，主要是因为通入气体后的水-气-油絮体密度小于水-油絮体密度，使水-气-油絮体在受到离心力的作用时更容易做向心运动，说明在通入气体后有利于油滴从油-水混合物中分离出来。通入气体后的轴向速度远大于未通入气体时的轴向速度且存在一定的分布规律，通入气体后形成的微气泡因数量多、比表面积大，在吸附油滴后可形成高孔隙度、无规则形状的微气泡-油滴絮体，当切向速度和径向速度在合适的大小时即可快速上浮至装置顶部除去。

图7 气体含量对速度分布的影响Fig.7 Effects of gas content on velocity distribution(a) Tangential velocity (inlet flow 600 L/h); (b) Axial velocity (inlet flow 600 L/h) Height 400 mm, with 10% volume fraction air; Height 400 mm, without air; Height 1050 mm, with 10% volume fraction air; Height 1050 mm, without air

3.4 进口流量及分流比对油污去除率的影响

进口流量与分流比对油污去除率的影响模拟结果见图8。由图8(a)可以看出，随着处理量的提高，模拟得到的油污去除率先提高后降低，在模型混合物进口流量为550～600 L/h时达到最大，为0.856。这主要是因为在较低的处理量时，流体进入装置做旋流运动的切向速度太小，油滴未能从油-水混合物中脱离出来就随流体从装置底部逃逸，且在较低的进口流量下，不利于形成稳定的离心力场，微气泡无法捕获油滴粒子形成微气泡-油滴絮体。虽然较高的进口流量可以带来较大的切向速度，有利于形成旋转流场，促使油滴和微气泡做向心运动，但是较高的进口流量会带来较大的剪切速率，容易造成微气泡-油滴絮体在其最薄弱的结合点处断裂成为更小的絮体，不利于微气泡-油滴絮体的稳定存在，从而影响其处理效率。由图4(b)可知，在同一截面高度处切向速度随着进口流量的增加而增加，切向速度的大小影响油滴从油-水混合物中脱离出来所需时间的长短。因此，随着进口流量的增加，装置对油污的模拟去除率提高；但是过大的进口流量带来过大的剪切速率，破坏微气泡-油滴絮体的形成造成去除率下降。

分流比在一定程度上影响装置对油污的去除率。由图8(b)可以看出，在分流比为10%～12%时，油污去除率达到最大为0.911。较小的分流比引起的湍流波动足以导致絮体破碎，且小颗粒絮体受到的外力与自身内力会促使小颗粒絮体聚并成为大粒径絮体，有利于油污的去除，表现为去除率随分流比的增大而提高。分流比过大时内部流体发生强烈湍流波动，导致稳定的絮体破碎，产生的子颗粒絮体更难聚并成为大粒径絮体，造成去除率降低，表现为去除率随分流比的增大而降低。

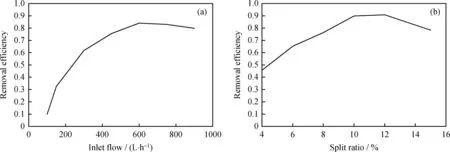
图8 进口流量和分流比对油去除效率的影响Fig.8 Influence of inlet flow rate and split ratio on oil removal efficiency(a) Inlet flow vs. removal efficiency (with 10% volume fraction air, split ratio 10%);(b) Split ratio vs. removal efficiency (with 10% volume fraction air, inlet flow 600 L/h)

4 结 论

(1)通过数值模拟，分析了不同进口流量带来的流场速度的变化，在进口流量过小或者过大时，均不利于装置对油污的去除，最佳模型混合物进口流量区间为550～600 L/h。

(2)在合适的进口流量下，对注气前后的速度场进行对比发现，通入微气泡有利于对油滴的去除。模型混合物的分流比影响油污的去除率，最佳分流比区间为10%～12%，去除率最大可达到0.911。

符号说明：

Cd——单位质量曳力系数；

do——油滴颗粒直径，μm；

Fgl——气、液两相间综合作用力，N；

Q——进口流量，L/h；

Re——相对雷诺数；

S——进口截面面积，m2；

v——流体速度，m/s；

vo——油滴速度，m/s；

ε——湍动能耗散率；

μ——流体黏度，Pa·s；

ρ——密度，kg/m3；

τ——应变张力，N。