复杂动态网络自适应有限时间同步控制
石宇静,李 强
(哈尔滨理工大学应用数学系,黑龙江哈尔滨 150080)
1 引言
在过去的十多年,复杂动态网络受到了越来越多的关注和研究.一方面,复杂网络普遍存在于生活中,如互联网、万维网、神经网络[1]等等;另一方面,复杂网络在物理、科技、生命科学等领域均具有广泛的应用价值[2].因此,深入研究复杂网络具有重要的现实意义.
同步作为自然界中普遍存在的一种现象,已经被人们广泛关注.近些年,针对复杂动态网络同步的研究有了很大的进展[3].目前,复杂动态网络同步的研究方法主要有滑模控制[4]、牵制控制[5]、脉冲控制[6-7]、间歇控制[8]等方法.然而,在实际中系统的某些参数往往是未知的,自适应控制方法则可以在系统参数未知的情况下,设计自适应控制器,通过自适应律进行不断的参数调整,对所研究的系统进行实时有效地控制.如文献[9-12]针对参数未知复杂动态网络给出了自适应控制器设计方法.
上述同步的研究均是针对复杂动态网络渐近同步和指数同步的研究结果,即误差动态系统的运动轨迹在时间趋于无穷时达到平衡点.但是,在实际的工程中,人们更希望误差动态系统能够在有限时间内达到平衡点,这样可以节约时间和成本,更有实用价值.因此,近些年复杂动态网络的有限时间同步问题被很多学者关注,并且取得了一些研究成果见文献[13-18].其中,文献[13]针对网络节点间的耦合是非线性耦合时,研究复杂动态网络有限时间同步的牵制控制器设计方法,并且同步过渡时间的估计值不依赖于初始条件.文献[14]研究了时滞复杂动态网络的有限时间同步问题.文献[15]利用随机稳定性理论,研究了具有随机扰动的复杂动态网络有限时间同步控制方法.文献[16-18]利用非光滑分析和Filippov解的定义,研究了不连续复杂动态网络的有限时间同步控制问题.然而,在这些研究中,所设计的控制器都是要求网络的耦合权重是已知的,如果网络的耦合权重未知,那么这些控制器将不能够实现对复杂动态网络的有效控制.在实际中,复杂动态网络是由多个子节点组成的,而这些子节点间的耦合强度和拓扑结构是错综复杂的,这样使得网络的耦合权重往往是不可测和不可知的.因此,针对耦合权重未知复杂动态网络的有限时间同步控制的研究是一个具有挑战性的问题.
基于上述分析,本文研究了复杂动态网络的自适应有限时间同步问题.文章的主要贡献陈列如下:1)分别针对复杂网络的耦合权重已知和耦合权重未知两种情况,利用自适应控制方法设计相应的自适应控制器和自适应律;2)所引用Lipschitz条件中,不同于已有文献如[16-17]等要求参数ηi已知,本文的参数ηi可以是未知的;3)在网络权重未知的情况,在Filippov解的框架下,给出了不连续的非线性自适应控制器设计方法;4)基于有限时间稳定性理论,证明了本文所设计两种自适应控制器均能保证同步误差系统是有限时间稳定的,并且给出了同步过渡时间上界的估计.
2 模型描述
考虑如下复杂动态网络模型:
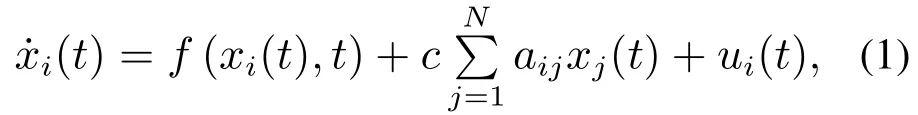
其中:xi(t)=[xi1(t) xi2(t)··· xin(t)]T∈Rn,ui(t)∈Rn分别表示第i个节点的状态向量和控制输入,
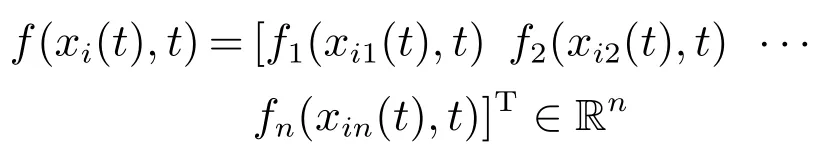
表示连续的向量值函数.常数c和aij分别表示耦合强度以及网络的拓扑结构,其中aij>0表示第i个节点与第j个节点间有连接,否则aij=0,且满足

令L=(lij)N×N,其中lij=caij.
令s(t)是复杂动态网络中孤立节点的一个解,假定它是唯一的并且满足
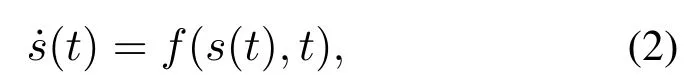
其中s(t)=[s1(t) s2(t)··· sn(t)]T∈Rn可以是一个平衡点,一个非平凡周期轨道或是一个混沌轨道.
定义同步误差ei(t)=xi(t)−s(t),由
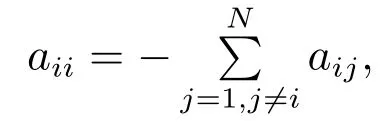
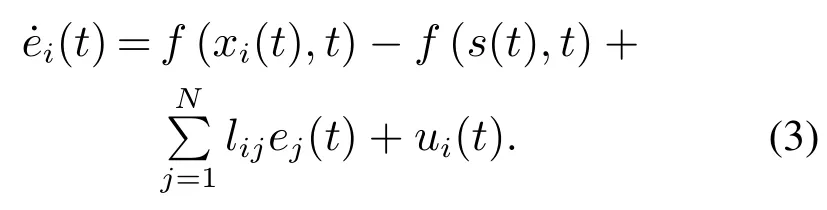
定义1对于复杂动态网络(1),如果存在一个时刻t∗>0,满足
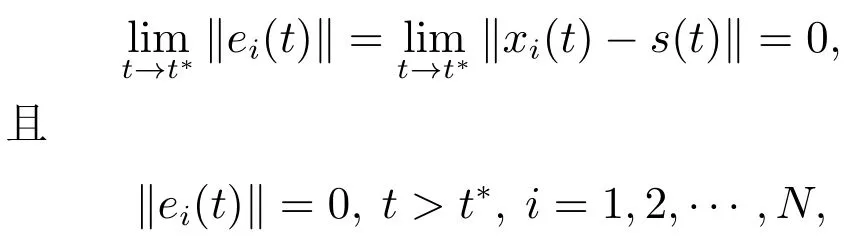
其中‖·‖表示向量范数,则称复杂动态网络(1)与目标系统(2)在有限时间内达到同步.
引理1[19]假设V(t)是连续的正定函数,如果存在连续函数γ,且γ(σ)>0,σ∈(0,+∞)满足
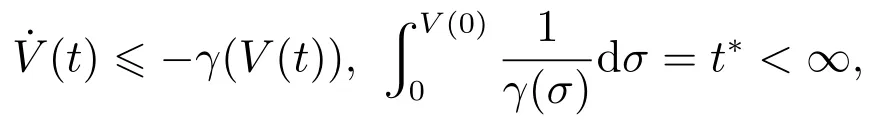
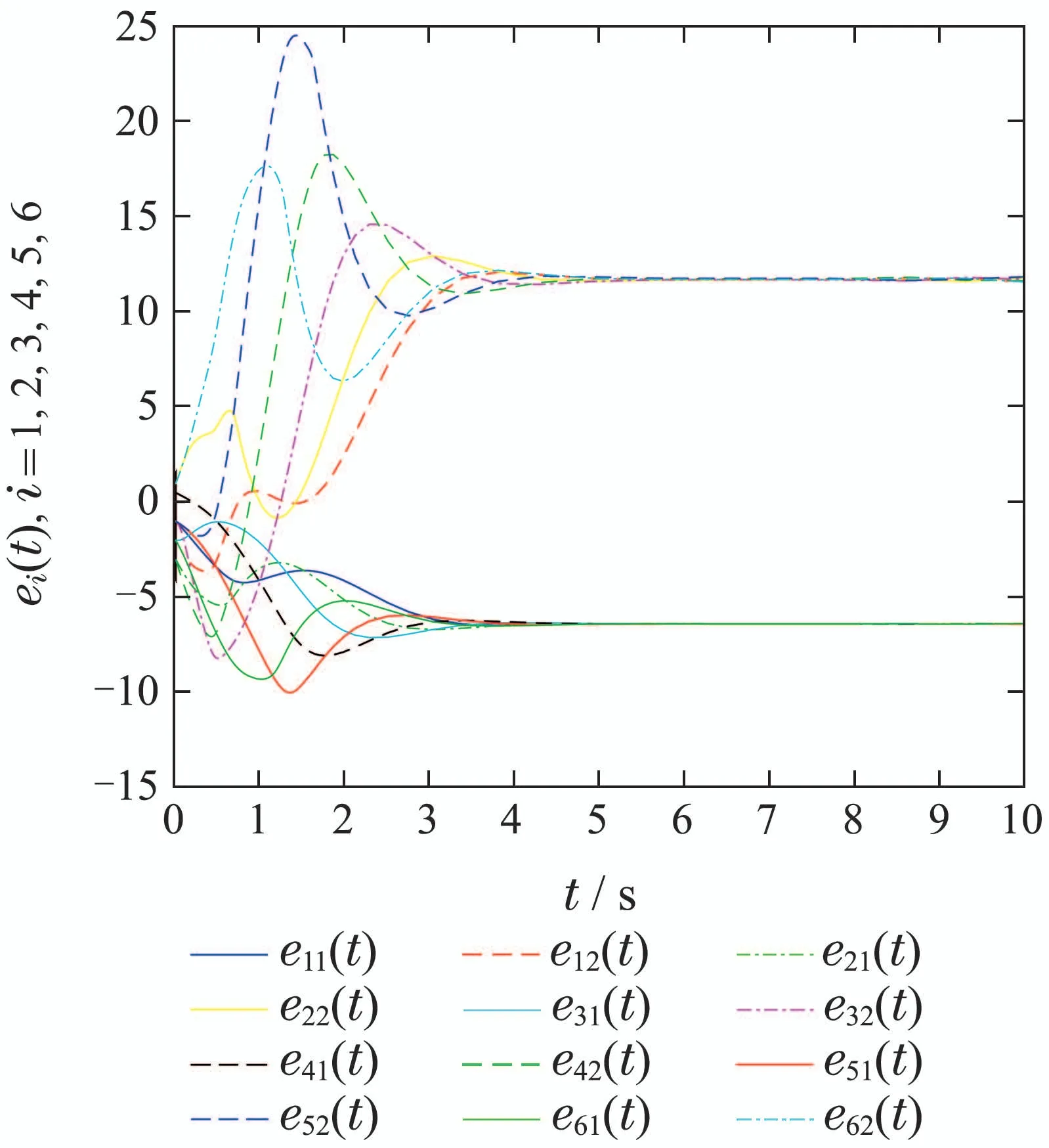
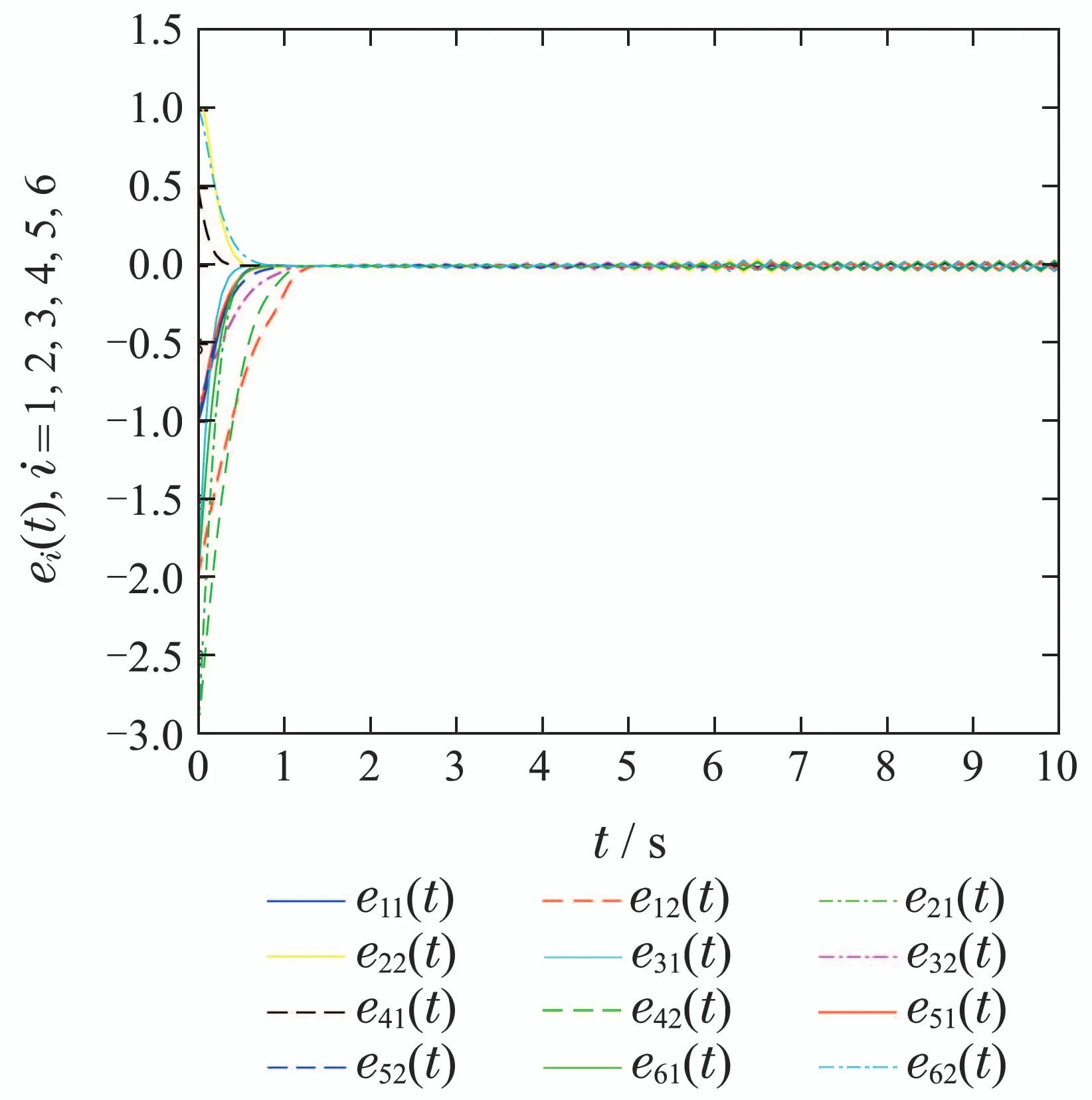
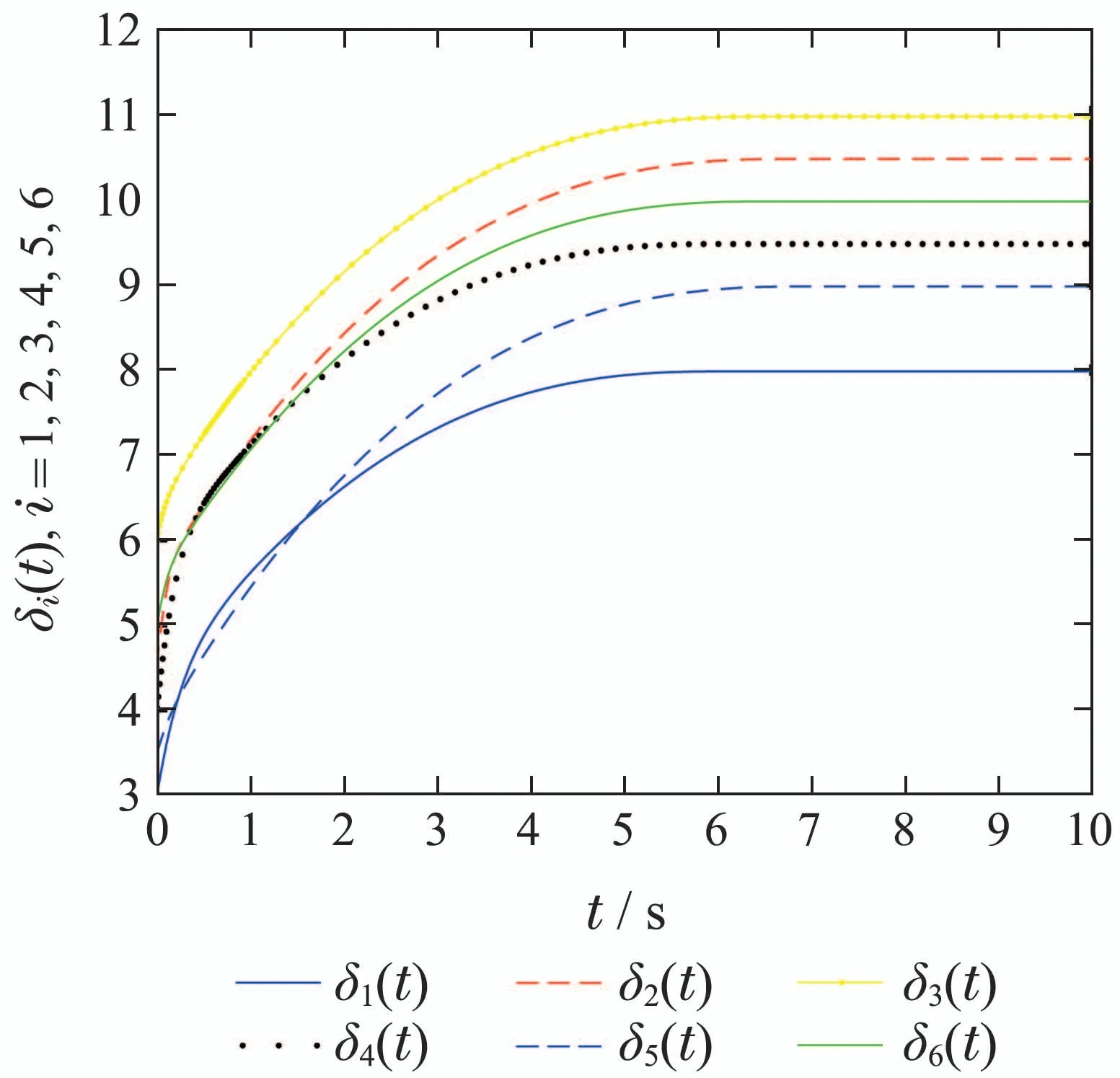
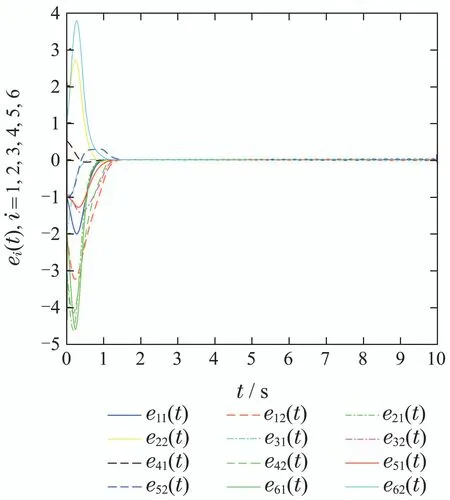
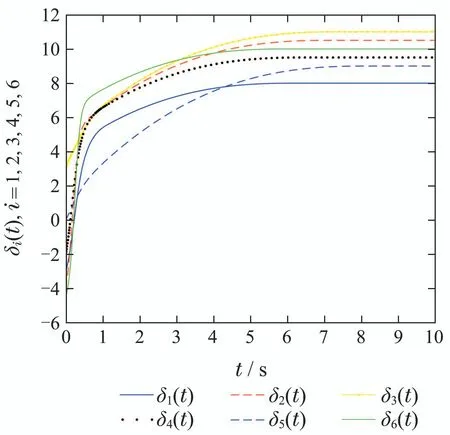
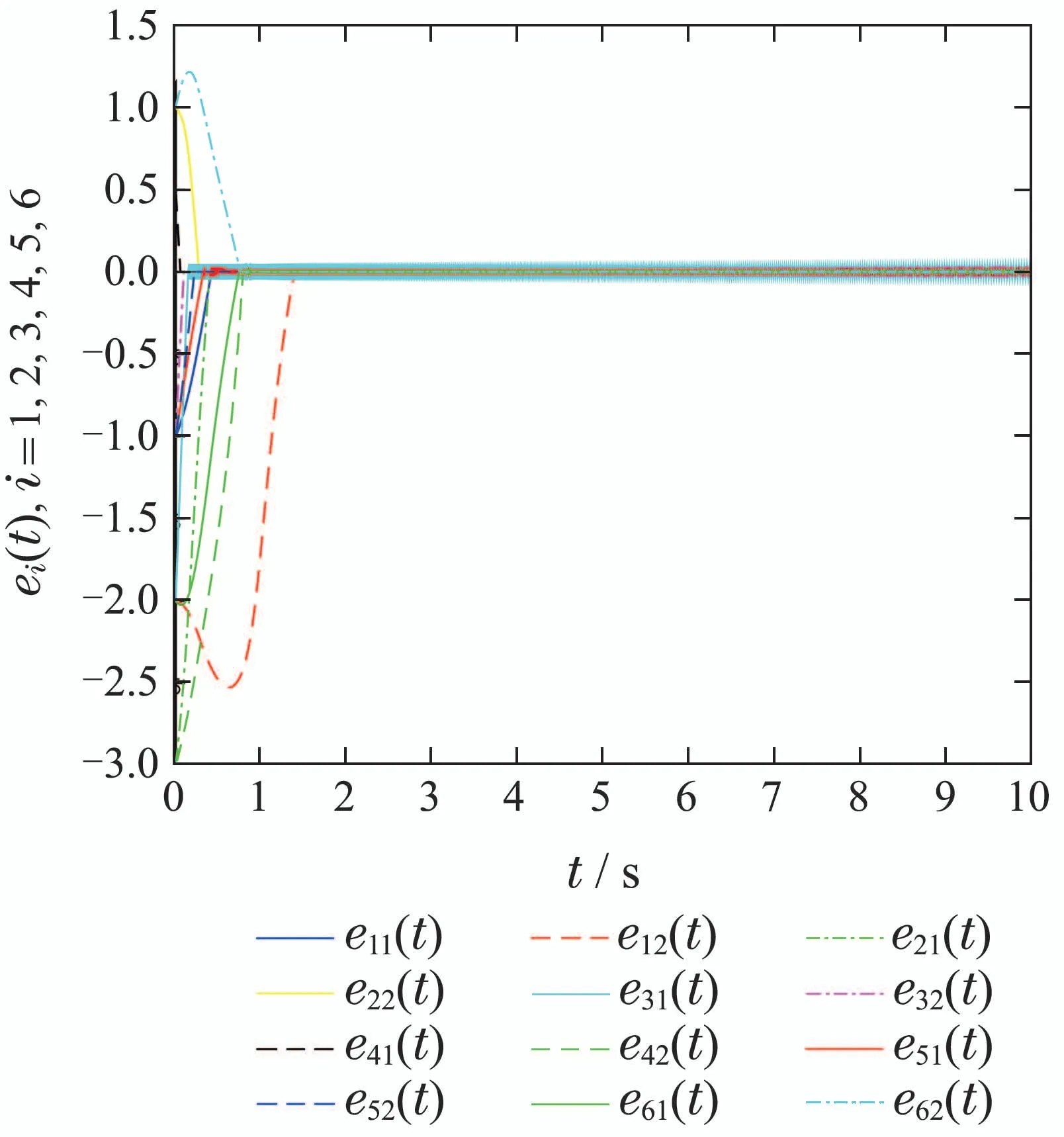
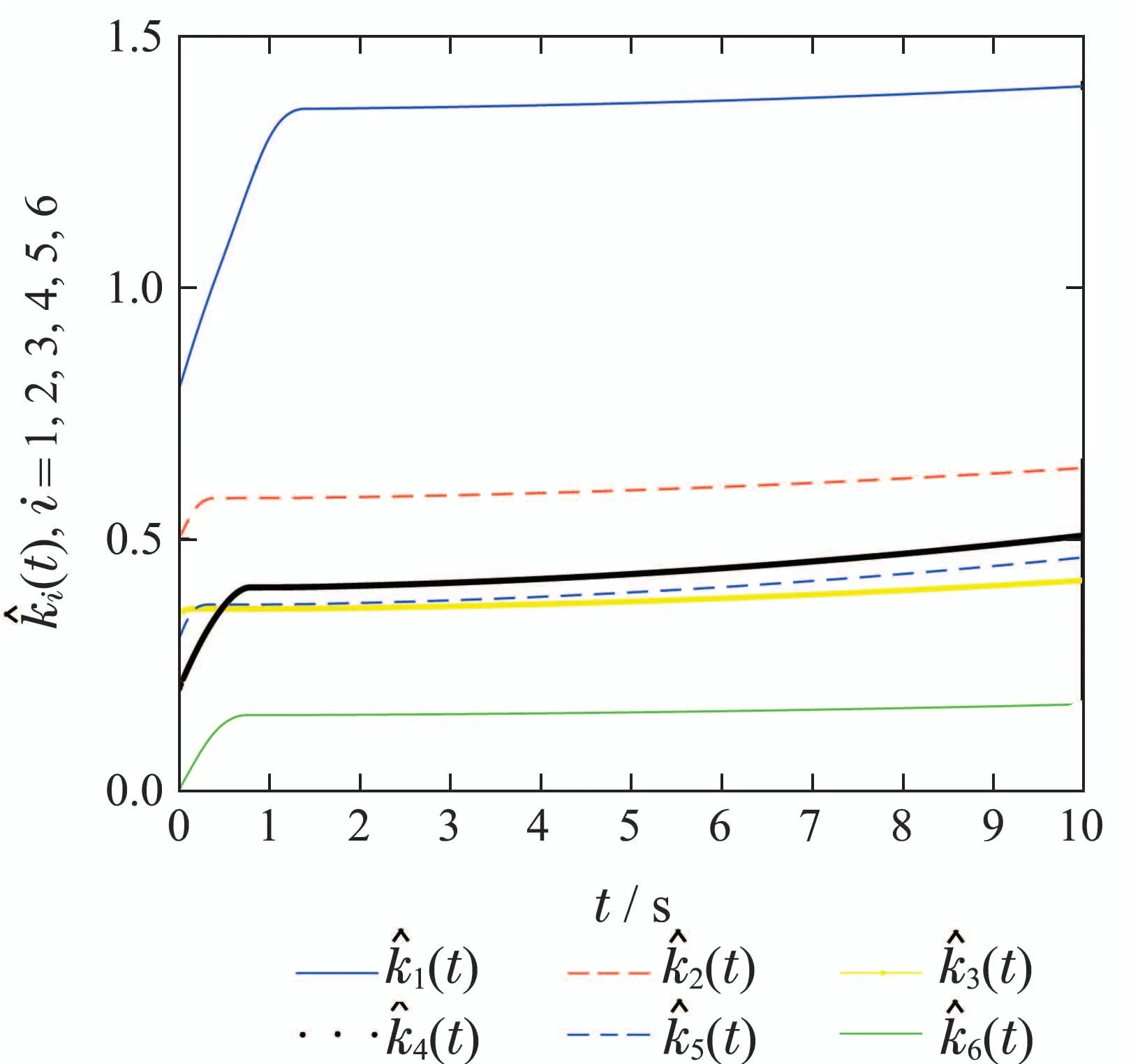
则有V(t)≡0,∀t ≥t∗.如果γ(σ)=dσq,且d>0,0 引理2[17]如果a1,a2,···,an,r,p 为实数且满足0 对于复杂动态网络(1)满足如下假设条件: 假设1非线性函数fj(xij(t),t)(i=1,···,N,j=1,···,n)满足Lipschitz条件,即存在一个常数ηi>0,对于任意不同的xij(t),sj(t)∈R满足 在此小节,假设复杂动态网络(1)中的耦合权重lij和参数ηi是已知的.设计自适应控制器使得复杂动态网络(1)和目标系统(2)能在有限时间内达到同步.为了实现这一目的,设计如下自适应控制器: sgn(·)表示符号函数,且控制增益αi>0,常数0<µ<1. 设计自适应律为 定理1在满足假设1的条件下,复杂动态网络(1)和目标系统(2)的状态在自适应控制器(4)和自适应律(5)的作用下是有限时间同步的,并且同步过渡时间满足 证选取如下Lyapunov函数: 计算V1(t)沿系统(3)的导数并考虑假设1成立,则有如下式子成立: 红军在茂县收购粮食,每斗玉米(约40斤)付给银元四至五元。茂县苏维埃每天在县城附近地带为红军筹粮,有时候一天可筹集四五千斤。城西区苏维埃每天也可为红军筹粮约1000斤。 计算V2(t)沿系统(3)的导数,且代入自适应律(5)有如下式子成立: 结合式(8)-(9)并利用引理2,可得 证毕. 由引理1可知,在自适应控制器(4)和自适应律(5)的作用下,复杂动态网络(1)与目标系统(2)能够在有限时间内达到同步,而且同步过渡时间满足式(6). 首先给出几个本小节用到的有关集值映射和Filippov解的引理. 引理3[20]假设E ⊂Rn,如果对每个点x∈E,对应一个非空子集F(x)⊂Rn,则称映射x→F(x)是从E→B(Rn)的集值映射,其中B(Rn)表示Rn中的所有子集. 引理4[20]对于右端不连续系统 定义如下Filippov集值映射: 函数V:Rn→B(Rn)的广义梯度定义为 其中:co(·)表示凸包,ΩV⊂Rn是函数V 不可微点的集合,S是测度为零的集合. 定义V 在点x关于集值映射F(x)的集值Lie导数定义为 在此小节,进一步考虑复杂动态网络(1)中的耦合权重lij和参数ηi未知的情况下,设计自适应控制器使得复杂动态网络(1)和目标系统(2)能在有限时间内达到同步.对系统做如下假设: 假设2令ki=ηi+,其中,存在常数>0满足|ki|≥. 复杂网络耦合权重未知时,设计如下自适应控制器: 其中: sgn(ei(t))=[sgn(ei1(t))··· sgn(ein(t))]T,φ(ei(t))的定义同式(4),控制增益βi>0,ϖi>0,常数0<µ<1,是未知参数ki的估计. 自适应律设计如下: 其中:ρi>0为常数,‖ei(t)‖1=为向量的1-范数. 定理2在满足假设1和假设2的条件下,复杂动态网络(1)和目标系统(2)的状态在自适应控制器(12)和自适应律(13)的作用下是有限时间同步的,并且同步过渡时间满足 证将控制器(12)代入同步误差系统(3)可得 由于系统(15)包含不连续项sgn(ei(t)),令函数gi(t)表示同步误差系统(15)的右边函数,且g(t)=.由Filippov规则,可得 选取如下Lyapunov函数: 为参数估计误差. 计算V(t)关于式(16)的集值Lie导数: 由假设1和SGN的定义可得 将式(19)-(21)代入式(18)可得 根据假设2,容易得到 将式(23)代入式(22),并利用引理2可得 证毕. 由引理1 可知,在自适应控制器(12)和自适应律(13)的作用下,复杂动态网络(1)与目标系统(2)能够在有限时间内达到同步,而且同步过渡时间满足式(14). 考虑含有N=6个节点的复杂动态网络(1),其耦合矩阵如下: 选择非线性函数f(xi(t),t)=Bψ(xi(t)),其中: 图1给出了复杂网络(1)与目标系统(2)在没有控制作用时,误差动态系统的误差轨迹.从图1可以看出若不对复杂网络进行控制,复杂网络(1)和目标系统(2)的状态无法达到同步. 图1 无控制作用时同步误差ei(t)Fig.1 Synchronization errors ei(t)without control 情形1考虑复杂动态网络(1)中的耦合权重lij和参数ηi是已知的.根据定理1利用自适应控制器(4)和自适应律(5)作用于复杂网络.选择复杂动态网络(1)和目标系统(2)的初值条件分别为 图2 控制器(4)作用下同步误差ei(t)Fig.2 Synchronization errors ei(t)under controller(4) 图3 自适应参数δi(t)Fig.3 Adaptive parameters δi(t) 图2描述了复杂动态网络与目标轨迹之间有限时间同步误差的变化曲线,图3显示了自适应参数δi(t)(i=1,···,6)的变化轨迹. 为了进一步说明所设计的自适应控制器的优势,本文将自适应控制器(4)与文献[14]所设计的如下反馈控制器做对比: 其中:ωi=0.1,τi=0.2,i=1,···,6. 利用文献[14]的控制器设计方法,其仿真结果如图4所示.对比可知,利用文献[14]的控制器也可以实现对复杂动态网络和目标轨迹的同步控制.但是,在文献[14]所给的控制器作用下复杂网络达到同步所需的时间更长.因此,本文所设计的自适应控制器比文献[14]所设计的控制器收敛速度更快. 图4 在文献[14]控制器作用下同步误差ei(t)Fig.4 Synchronization errors ei(t)under controller of Reference[14] 接着,本文改变自适应律(5)中自适应参数δi(t)(i=1,···,6)的初始条件为δ1(0)=−3,δ2(0)=−4,δ3(0)=3,δ4(0)=−2,δ5(0)=0,δ6(0)=−4.5,其他参数同上所述,不做改变.得到仿真结果如图5-6所示.将图5-6与前面的图2-3相比较可知,改变自适应律的初始条件,对同步误差轨迹的收敛速度影响不大. 图5 改变自适应律(5)的初始条件同步误差ei(t)Fig.5 Synchronization errors ei(t)under changing initial condition of adaptive law(5) 图6 改变自适应律(5)的初始条件自适应参数δi(t)Fig.6 Adaptive parameters δi(t)under changing initial condition of adaptive law(5) 情形2考虑复杂动态网络(1)中的耦合权重lij和参数ηi是未知的,那么根据定理2,利用自适应控制器(12)和自适应律(13)作用于复杂网络,复杂网络和目标系统的状态初始条件选择同上,选择自适应更新律(13)的初值 选择控制器参数为 仿真结果如图7-8所示.图7描述了复杂动态网络与目标系统的同步误差变化曲线,从图7中可以看出,所设计的自适应控制器(12)可使同步误差在有限时间内快速的收敛到平衡点.图8显示了未知参数估计的变化曲线. 图7 控制器(12)作用下同步误差ei(t)Fig.7 Synchronization errors ei(t)under controller(12) 图8 未知参数估计Fig.8 Estimation of unknown parameters 本文研究了复杂动态网络自适应有限时间同步控制问题.首先针对系统耦合权重lij和参数ηi已知的情况,设计了自适应控制器和自适应律,利用有限时间稳定性定理证明了复杂网络与目标系统在有限时间内达到同步.接着进一步考虑系统耦合权重lij和参数ηi均未知,设计了不连续的自适应控制器和未知参数的自适应律,利用微分包含原理在Filippov解的框架下,得到了复杂动态网络与目标系统有限时间同步的结论.最后,通过数值仿真验证了所提自适应控制策略的有效性.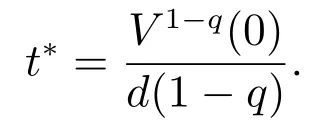
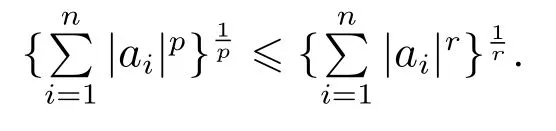
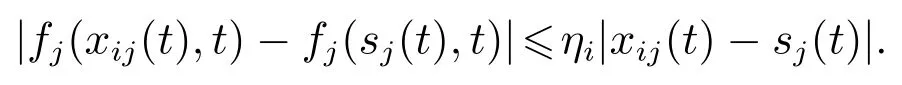
3 主要结果
3.1 耦合权重已知的自适应控制器设计

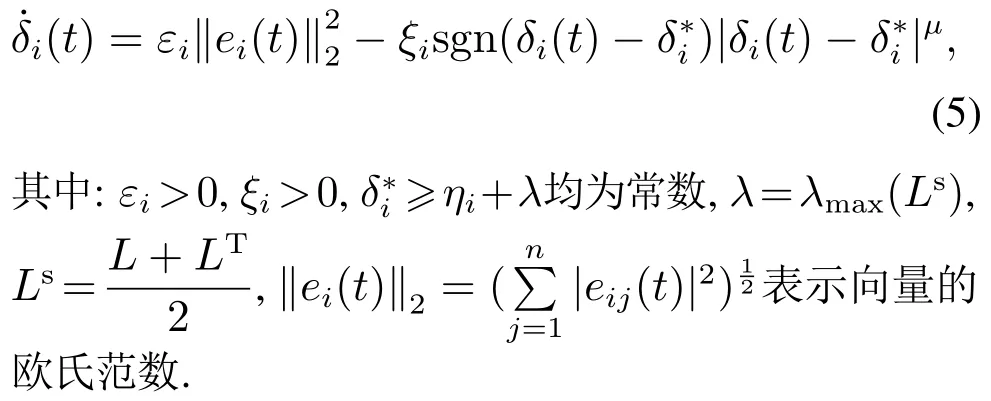
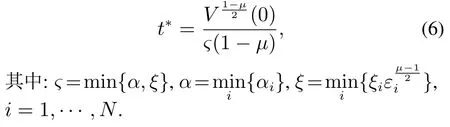
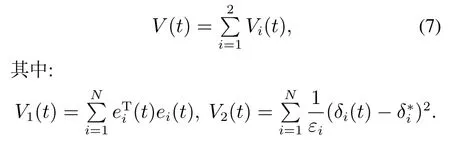

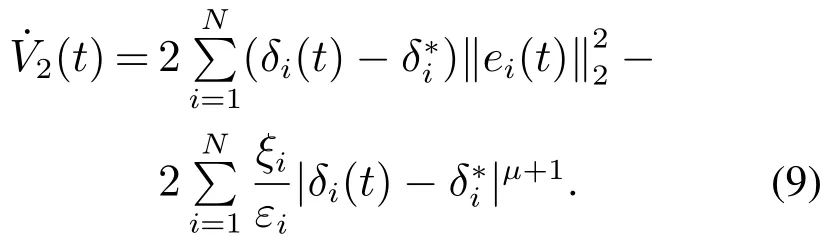
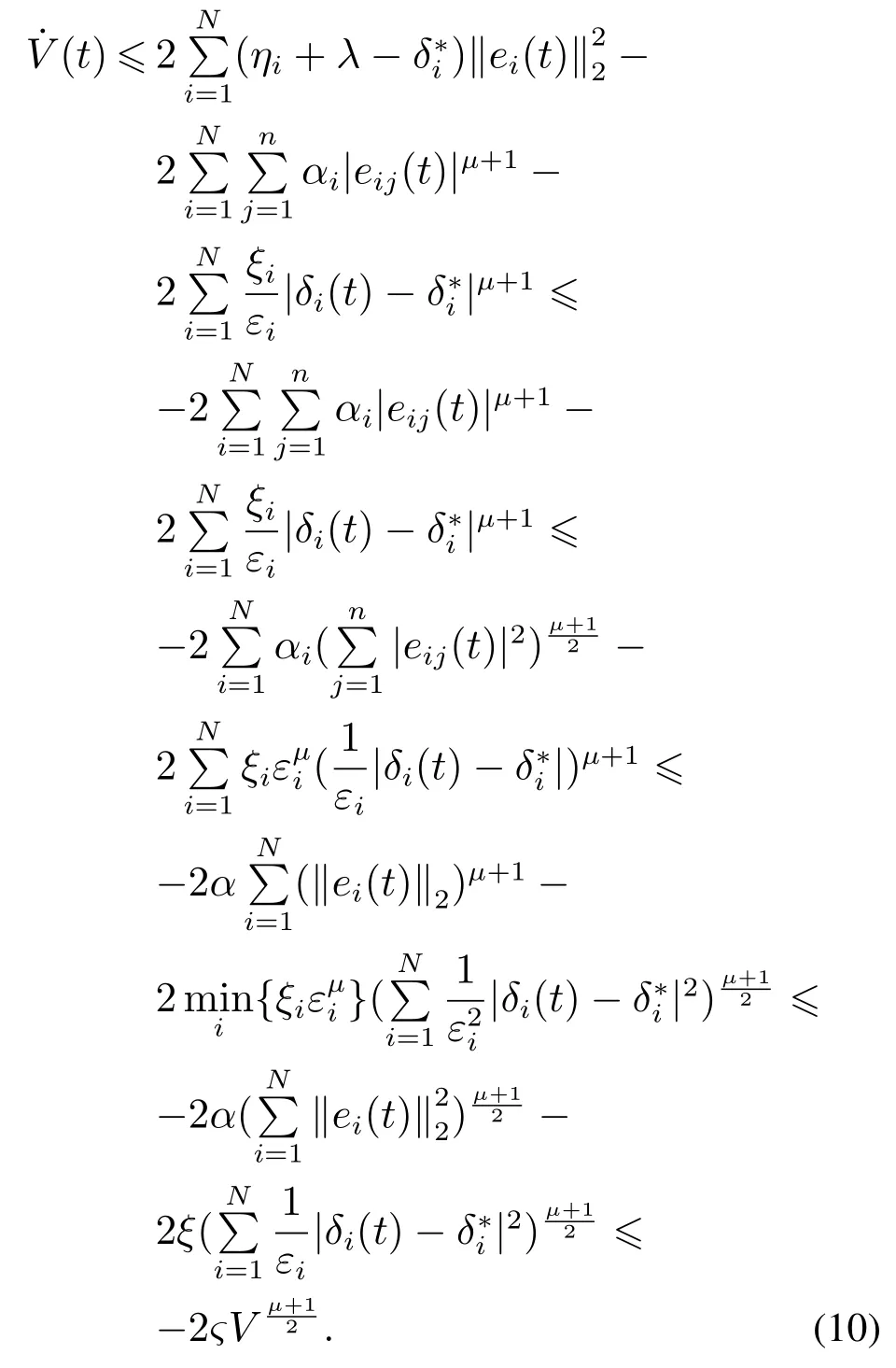
3.2 耦合权重未知的自适应控制器设计
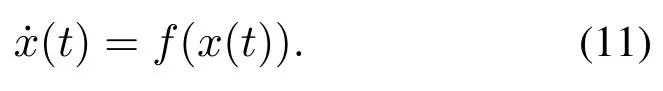
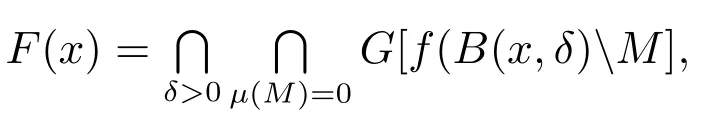
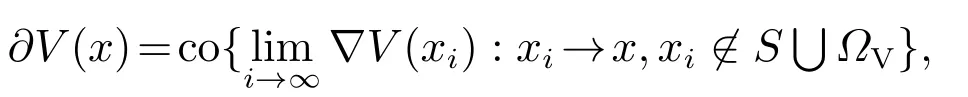
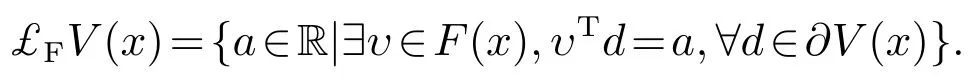
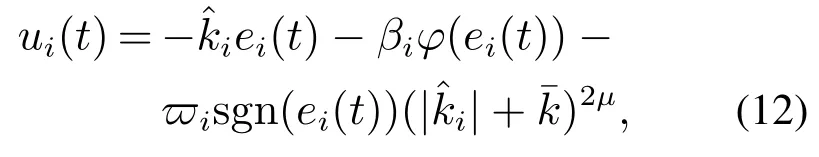
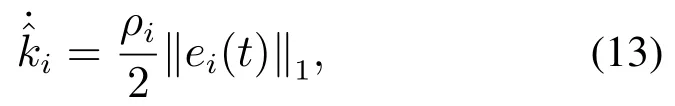
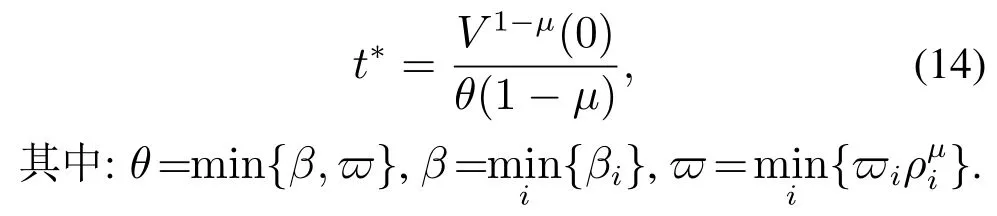
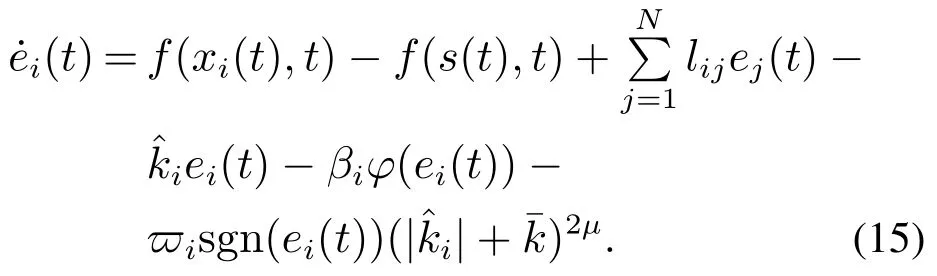
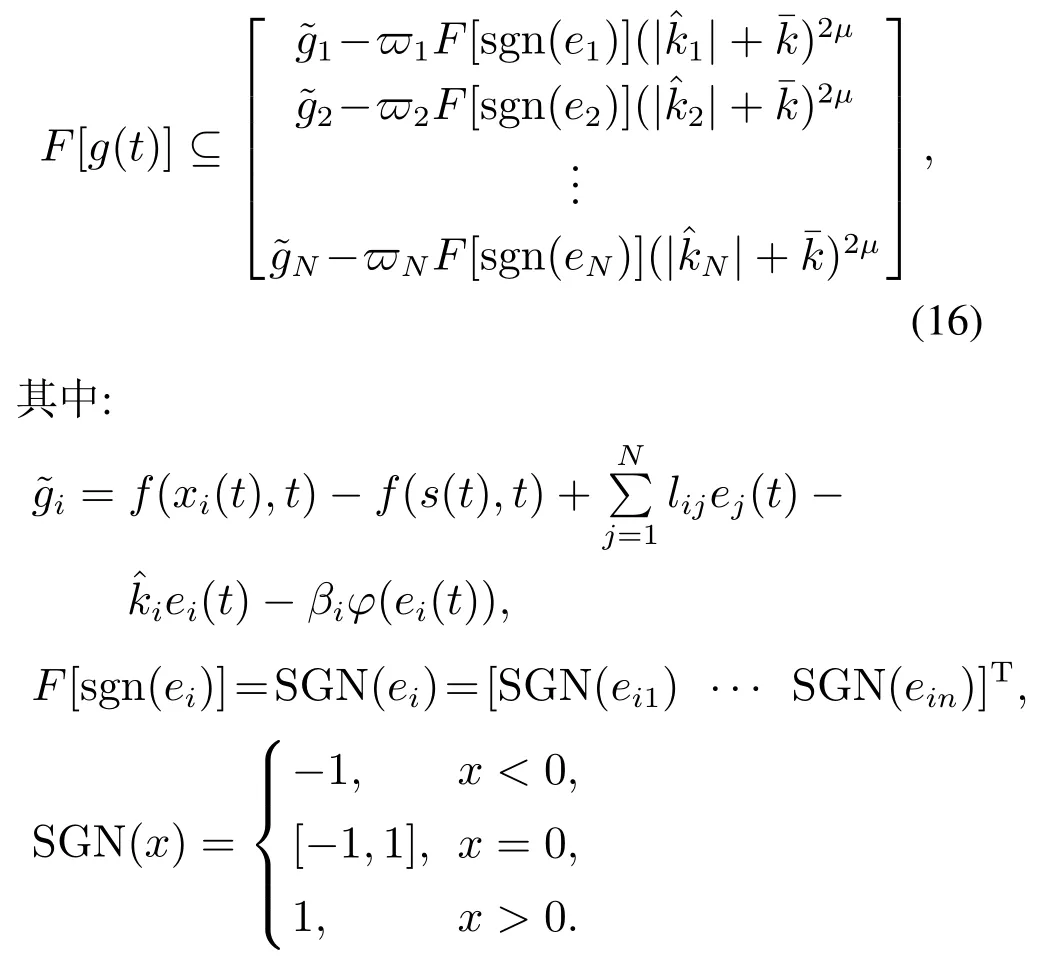


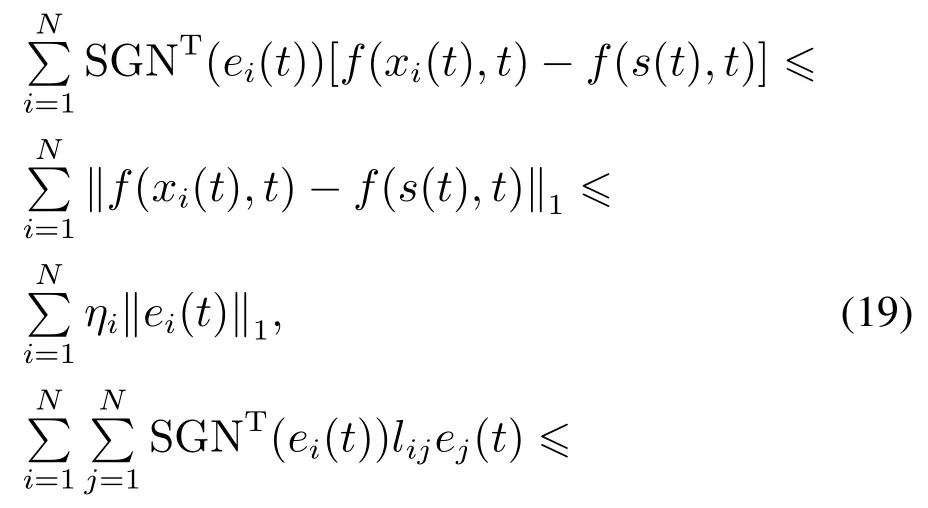
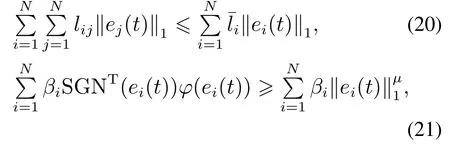
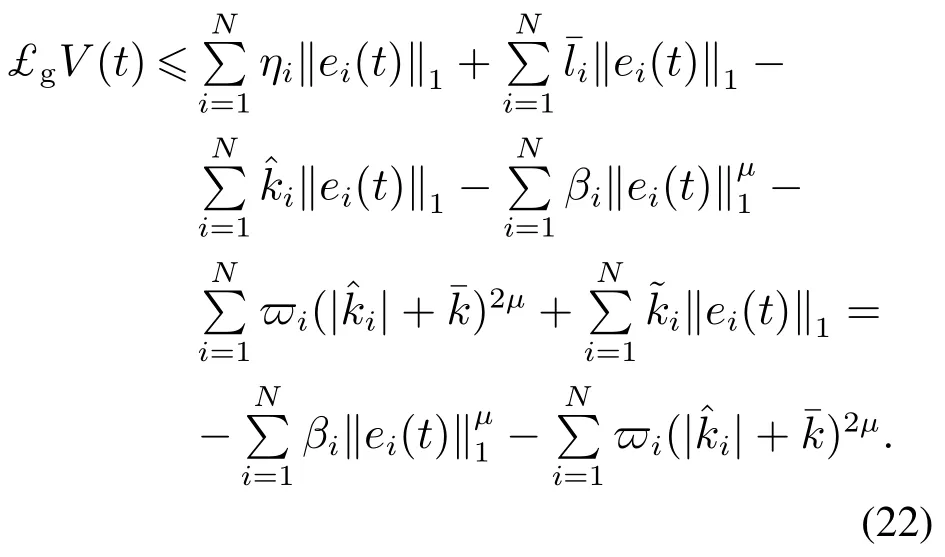
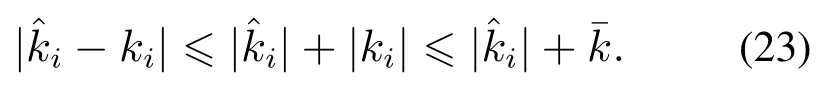
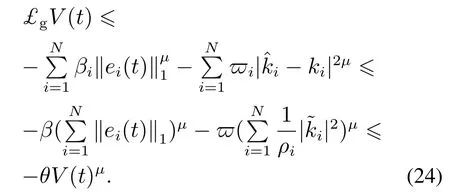
4 数值仿真
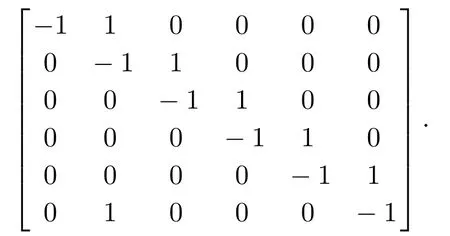
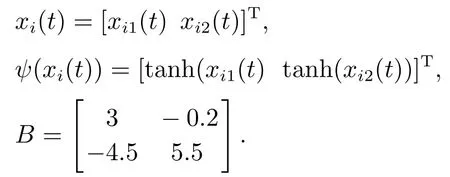

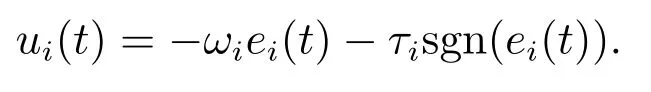

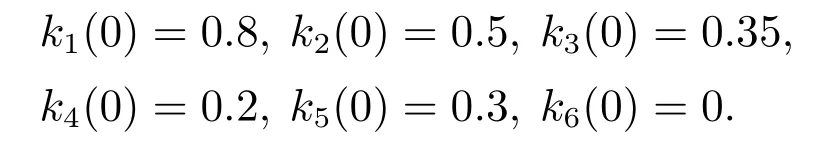
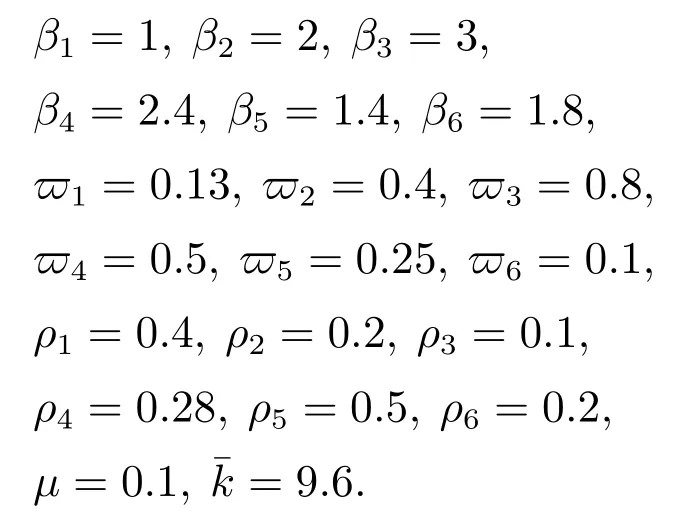
5 结论

