惯性导航系统可观测性分析与可观测状态确定的图方法

刘 鹏 任一峰 张 亚吴常铖

(1.中北大学电气与控制工程学院,山西太原 030051;2.中北大学仪器科学与动态测试教育部重点实验室,山西太原 030051;3.东南大学自动化学院,江苏南京 210096;4.南京航空航天大学自动化学院,江苏南京 211106)

1 引言

惯性导航系统(inertial navigation systems,INS)是一种利用惯性测量装置来测得运载体的运动加速度和角速度,并经过运算求出载体的位置和姿态的导航设备.这是一种自主式的导航系统,不需要任何外界信息,只依靠自身的测量装置.由加速度经过积分运算得到速度与位置时,必须要用到初始速度和初始位置.为了避免平台误差引起加速度测量的误差,需要对平台进行指向对准,这个过程称为INS的初始对准.初始对准是INS正常工作的重要条件[1],实质上是确定惯性器件输入轴与INS所采用的坐标系之间关系的过程.对于平台式INS,在系统加电启动后,其3个框架轴的指向是任意的,必须通过调整使得陀螺仪的敏感轴对准惯性导航坐标系,以便为加速度计的测量提供基准.对准中常提到的两个重要指标是对准精度和对准速度.其中,对准精度直接影响导航的性能,而对准时间的长短也是评价相关性能的一个重要指标.为了在初始阶段使INS达到较高的对准精度和对准速度,需要在建立准确的INS误差模型的同时,对误差因素进行分析,从而减小或消除误差.从控制理论的观点看,初始对准的主要困难在于INS的误差方程是不完全可观测的.文献[2]指出利用矩阵论方法对INS初始对准误差动态方程进行可观测性分析时,适时地选择状态变量以及划分状态空间来确定可观测的状态分量,可以提高初始对准的有效性,合理解决对准时间与对准精度之间的矛盾.INS的误差模型是一种时变系统,可以借助线性系统理论的已有结论[3],来对这种系统的可观测性进行分析.研究可观测性的原因在于系统的可观测性(可检测性)条件是Luenberger观测器或Kalman滤波器运行的前提[4].当模型中的角度误差变化不大时,可以把静基座时的误差系统模型看作是线性时不变的,这时利用卡尔曼滤波技术能够对可观测的系统状态给出最优的估计[5].但对于动基座时的误差模型,一般视其为时变系统,为了简化对时变系统的分析,Goshen-Meskin等人在文献[6]中系统性地研究了分段定常系统的可观测性,进而利用这种分段定常的方法来研究动基座时INS的可观测性[7],文章指出载体的机动性可以增强系统的可观性.Jiang Y.F.等人在文献[8]中利用状态方程解耦法来分析平台式INS的可观测性.对于捷联惯性系统对准时的可观测性问题,文献[9]给出其非线性时的结论.近年来,由于卫星导航系统的出现,多位学者[10-13]对全球定位系统(global positioning system,GPS)和INS组合系统的可观测性进行了分析.Rhee对时变系统的可观测进一步划分为:完全可观测,区别可观测和瞬时可观测.利用时变系统的可观测性矩阵来分析此系统的可观测性[10].Hong S.等人进一步指出改变载体的加速度可以增强姿态和陀螺偏差的估计,角速率的改变则改进了杠杆臂的估计[11].Ma Y.H.等人利用解耦法将18-维的INS/GPS的组合系统转化为3个6-维的子系统来分析其可观测性[12].针对INS的可观测性问题,亦可利用运动学模型来研究,具体参考文献[14-18].Batista等人利用时变系统的Gramian矩阵和Lyapunov变换矩阵给出4种动态模型的可观测结论和相应判据[14].文献[15]分析了具有单个距离辅助导航系统的可观测性.对于INS,有时仅关心部分状态的信息,文献[16]分析了此时的可观测性并给出相应的滤波器.文献[17]对长基线导航系统的可观测性进行了分析,同时设计了具有全局指数稳定的滤波器.基于Gramian矩阵对系统进行可观测性分析的方法亦可以进行传感器布控[19].信息理论也可以用来对INS进行可观测性分析[20].

INS的误差方程在静基座和动基座时,由于矩阵的部分元素含有纬度参数,所以此时可以认为系统矩阵具有微小变化,进而将系统矩阵的元素看作是具有结构的量:零或者非零元素.这样,可以利用结构可观测的判断方法来分析INS的可观性与可观测状态.系统的结构可观测性与结构可控性之间是对偶的关系.结构可控性及其图论特征最早由Lin[21]在1974年提出,接着Shields等[22]将其推广到多输入系统.具体分析方法和结论,参考近期的综述文献[23].对于复杂网络系统,通常研究者关心的是节点之间存在的链接数目,而对具体的权值大小不予关心,故而可以利用结构化方法来分析复杂网络的可观测性[24].此外,文献[25]利用图的观点来分析仅具有方位角时的协同定位问题的可观测性.

本文结合近期的成果[25,28],利用图论的方法来重新分析INS的可观测性,其贡献主要有2点:首先,给出静基座时惯性导航系统可观测的二分图判断方法,通过对二分图中最大匹配的不可匹配点的分析,可以得到与文献[2,7]中相同的结果,利用图论进行分析,避免了大量的数值计算,分析过程简单明了.其次,基于分段定常系统的分析法,建立其在结构化意义下的动态图表示框架,给出动基座时INS的可观测性判断和可观测状态确定的动态图和广义二分图方法,得出动基座时系统仍为不可观测的结论.

文章的组织结构如下:第2部分,首先建立方阵与其图论的表示方式,其次对文章中要用到的相关定义和结论以引理的形式给出.第3部分,分别给出静基座和动基座时的惯性导航系统的状态方程,针对不同的情形,用二分图的匹配和动态图的Menger-type linking给出系统可观测性的图论判定和可观测状态的确定方法,并给出相应的分析结果.最后,给出本文的总结,指出该方法可以进一步来分析组合导航系统的结构可观测性和可观测状态.

2 准备知识

这一部分给出方阵和系统的图论表示,以及文章中要用的一些图论知识和系统结构可观测的图论判据.

2.1 矩阵与图

矩阵A∈Rn×n称为结构矩阵是指其的元素或者为零或者为不确定的非零元素[21].对于结构化矩阵规定其运算如下:A1+A2=A,其中结构化矩阵A的不确定元素为aij当且仅当A1的元素或A2的元素为不确定元素.为了利用结构化理论,这里给出系统图G的表示形式.一般来说,系统图是一个有向图,有时亦称为流图.给定矩阵A,其不同的行与列分别对应不同的状态,如果A中的元素aij0,则存在从状态xj到状态xi的有向边(xj,xi).如果输出矩阵C∈Rm×n的元素ci,j0,则存在从状态xj到输出(传感器)yi的有向边.即系统有向图G可以表示为GA,C=(V,E),其中:

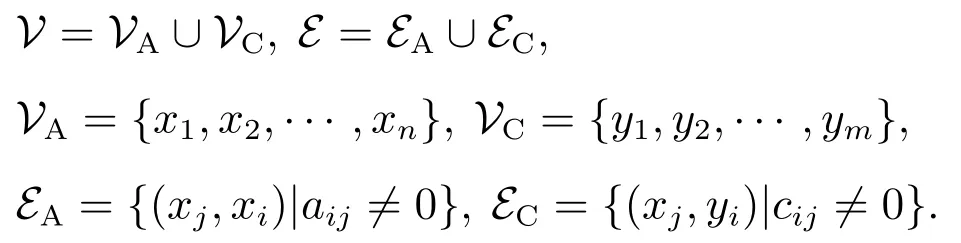
如果对于系统的任意状态节点(矩阵A对应的节点)都存在一条以某个输出(矩阵C对应的节点)为终点,且以这个状态为起点的有向通路,则说该系统为输出可达的.设V1和V2为互不相交的两个顶点集合,自集合V1到集合V2的有向边集为

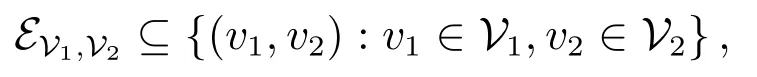
则称B(V1,V2,EV1,V2)为一个二分图.如果存在自集合V1中t个不同顶点到集合V2中t个不同顶点的t条不同有向边,则称这t条有向边构成的集合为二分图B(V1,V2,EV1,V2)的一个t-匹配,相应于此匹配的左或右节点称为左或右匹配节点.自集合V1到集合V2的所有不同有向边构成一个最大的边集合,称该集合为二分图B(V1,V2,EV1,V2)的最大匹配.系统图GA,C的二分图记为BG(A,C),其左边顶点集为VA,右边顶点集为VA∪VC,边集为矩阵A和C中的非零元素表示的有向边.

为了方便理解,这里针对上述系统图及其对应的二分图给出一个例子来进行说明.

例1考虑线性结构化系统

其中系统矩阵A∈R3×3和观测矩阵C∈R1×3分别具有下述形式:

其系统图和对应的二分图如图1所示,这里圆形节点表示状态节点(其中节点1,2,3分别表示状态分量x1,x2,x3),三角形节点表示输出节点(一般指传感器).图1的左边是这个系统对应的系统图,所有的状态节点都可以到达输出节点,故这个系统是输出可达的.图1的右边是相应系统图的二分图,其中自左边节点到右边节点集的任意一条有向边,如(x1,x3),称为这个二分图的1-匹配.任意两条有向边,如(x1,x3),(x2,x1),称为这个二分图的一个2-匹配.显然这个图中存在两个最大匹配:(x1,x3),(x2,x1),(x3,x2)和(x1,y1),(x2,x1),(x3,x2).这里可以看出,给定一个二分图,其对应的最大匹配是不唯一的,但其最大匹配所含有的边数是唯一的.

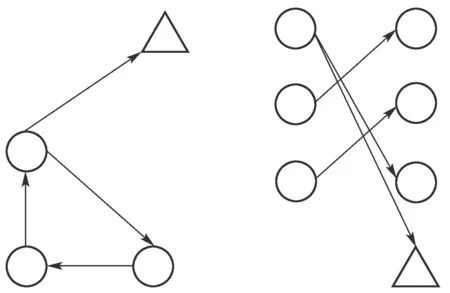
图1 系统图及其二分图Fig.1 System graph and its bipartite graph

2.2 相关引理

对于一般线性连续时不变系统这里给出其在结构化意义下的可观测性判据,并给出连续时变系统的分段定常处理方法和可观测性判据.

考虑结构化意义下的线性连续时不变系统:

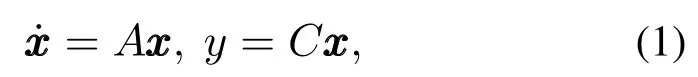
其中A∈Rn×n和C∈Rm×n为系统矩阵和输出矩阵.下面给出其结构可观测的定义.

定义1[21-22]如果存在与矩阵对(A C)具有相同结构1一般地,称相同维数的矩阵对(A C)和( )具有相同的结构是指,如果矩阵(A C)的每一个固定(零)元素,矩阵( )的相应元素也是固定的(零),同时,对于矩阵( )的每一个固定(零)元素,矩阵(A C)的相应元素也是固定的(零).的完全可观测矩阵对(A0C0),则称矩阵对(A C)为结构可观测的.

注1上述定义亦可表述为[26]:如果∀ϵ>0,存在与(A C)具有相同结构的完全可观测对(A1C1)使得‖A1−A‖<ϵ和‖C1−C‖<ϵ(其中‖·‖表示范数2例如,如果aij和bi分别为矩阵A和b中的相应元素,那么通常可以取‖A‖i,j=1,2,···,n=max|aij|和‖b‖i=1,2,···,n=max|bi|.)成立,则称矩阵对(A C)是结构可观测的.这个结果具有明显的物理意义.实际上,对于实际系统的矩阵对(A C),矩阵A和C的大部分元素是测量值的近似值.通常情况下,部分元素精确为零的位置是已知的.因此,这里假设矩阵A和C中的一些元素精确为零,其他元素为不确定的非零值具有合理性.

为了下面表述的方便,这里给出网络流中的两个概念,第1个概念是针对一般的有向图,第2个概念是对线性时不变系统来说的.

定义2(Menger-type linking[27])给定一个有向图,从顶点集合X到顶点集合Y 的顶点不交的有向路径称为自集合X到集合Y 的Menger-type linking,有向路径的数目称为链接的尺寸.

定义3[27-28]给定结构化线性连续时不变系统(1),称为系统(1)的时间跨度n的动态图,其中:

下面用一个例子来说明,给定结构化线性时不变系统后,如何绘制其动态图.

例2考虑例1中的结构化线性时不变系统.这里画出该系统对应的时间跨度3的动态图.图2中,X0为最左边的3个状态节点,X1=为第2列的3个状态节点,为最下面的2个输出节点,从X0到的Menger-type linking为着色有向路径和显然,在这个动态图中,不存在其它链接为3的有向路径.一般地,称这个自X0到的Menger-type linking为最大链接.

图2 例1的系统对应的动态图Fig.2 The dynamic graph associated with the system in example 1

下面的这个引理是系统结构可观测的图论判据.

引理1[22,24,27]设A和C分别是n×n和m×n的结构矩阵,以下命题是等价的:

1)系统(1)是结构可观测的;

2)i)GA,C是输出可达的;ii)二分图BG(A C)中存在一个n-匹配;

引理2[29]令A是有向图G的邻接矩阵(aij∈{0,1}),在矩阵Ar中,元素等于从顶点i到顶点j,含弧数为r条的相异有向链数.

引理3(Linkage lemma[27]) 设G=(X ∪U∪Y,A;X,Y)是一个具有入X和出Y 的有向图,BG=(X⋆∪U⋆,Y⋆∪U⋆;)为相应的二分图.那么,在G中存在一个自X到Y 的Menger-type complete linking当且仅当BG中存在一个完美匹配.

注2引理3中的入X是指顶点集合X中的节点只有出边,没有入边;相应的出Y 中的节点只有入边,没有出边.完美匹配是指,二分图中要么左边节点都为匹配的始点,要么右边节点都为匹配的终点.

对于线性时变系统,工程应用中可以将其视作不同阶段的线性时不变系统来处理.故而,这里给出分段线性定常系统(piece-wise constant system,PWCS)的一般结论.考虑下述PWCS[6]:

其中:Aj∈Rn×n,j=1,2,···,r,表示第j阶段的系统矩阵,C∈Rm×n表示不同阶段具有相同的输出矩阵.对YYY(t)进行求导数运算[1,6],并将这些向量堆积在一起可以得到

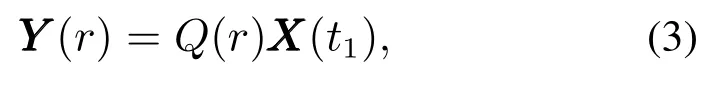
其中:t1为初始时刻,YYY(r)是包含全部观测向量及其逐次微分(直到n−1次)的总向量.矩阵Q(r)为

这里,∆j(j=1,2,···,r)为时间tj到tj+1的间隔,

为连续系统在第j时间段的可观测性矩阵.定义Qs(r)为连续PWCS的截取可观测性矩阵(stripped observability matrix,SOM):Qs(r)=

下面作为引理,给出连续PWCS的一个主要结论:

引理4[6]如果null(Qj)⊆null(Aj),1 ≥j ≥r,那么null(Q(r))=null(Qs(r)),rank(Q(r))=rank(Qs(r)).

上述引理中符号null(·)表示矩阵“·”的零空间,符号rank(·)表示矩阵“·”的秩.这个引理说明,在适当条件下,可以利用截取可观测性矩阵Qs(r)代替矩阵Q(r)来研究连续PWCS的可观测性.这样可以简化问题论述.

3 主要结果

这一部分研究两个问题:第1个问题是静基座下INS的可观测性分析和可观测状态的确定,利用的图论中的二分图匹配理论.第2个问题是动基座下INS的可观测性分析和可观测状态的确定,利用时变系统的分段线性定常分析方法和Menger-type linking知识,给出时变系统的结构可观测的图论判据,进一步给出广义二分图来分析动基座下惯性导航系统的可观测性.

3.1 静基座INS的可观测性

静基座INS初始对准的动态误差方程可写为[2]

δv1,δv2是速度误差沿东、北方向的投影;ϕ1,ϕ2,ϕ3是平台误差角沿东、北、天3个轴的投影;∇1和∇2是加速度计沿东、北向的零偏;ε1,ε2,ε3是陀螺沿东、北、天3个方向的漂移;参数ω是地球自转角速度;φ是当地纬度.

取惯性导航系统的水平输出速度误差作为观测值,即Zj=δvj+ωj,j=1,2,式中ωj表示白噪声.将上式写成矩阵形式如下:

通常情况下,对于给定的纬度参数,视系统方程(4)和(5)为时不变系统,此时可利用线性系统的理论来分析系统的可观测性.文献[1-2,7]在确定可观测状态时,取特殊的纬度值来分析.本文根据纬度参数的不同取值所引起的系统矩阵A中的元素为零与否进行分析.当纬度参数取值使得系统矩阵A中的某个元素为零时,系统图中该元素对应的边不存在;当纬度参数取值使得系统矩阵A中的某个元素为非零时,系统图中该元素对应一条有向边.进而通过用图论分析系统的结构可观测性的方法来分析静基座INS的可观测性,并确定可观测状态.

静基座INS(4)和(5)对应的系统图为图3,其中圆形节点表示状态节点,三角形节点表示输出(传感器)节点.

图3 静基座惯导系统的系统图Fig.3 System graph associated with the inertial navigation system under the stationary base

这个系统对应的二分图如图4所示.

图4 静基座惯导系统的系统二分图Fig.4 System bipartite graph associated with the inertial navigation system under the stationary base

图4中左边节点为有序状态节点,节点顺序与状态向量顺序一致.右边节点由复制状态节点和输出节点构成.左、右节点之间的匹配对应系统图中的有向边.

定理1静基座下惯性导航系统(4)和(5)是不完全可观;其可观测的状态数目等于系统图对应二分图中的最大匹配的数目;相应的可观测状态为系统二分图中对应最大匹配的左匹配节点.

证利用结构化理论来分析系统(4)和(5)的结构可观测性.定义=PC,其中P=diag{α1,α2},α1和α2为不确定的非零元素.因为∀α1,α20,等式

成立,所以上式左边矩阵与右边矩阵具有相同的秩.故,矩阵对(A C)和(A)具有相同的可观测性.将矩阵对(A)中的元素视为结构化元素,此时可以把数值意义下的可观测性转换为结构意义下的结构可观测性.由静基座惯性导航系统的系统图3可知,所有的状态节点都是输出可达的,故引理1的输出可达条件2)中i)成立.从图4中直接可以得出,最大匹配的数目为7,同时这个二分图的最大匹配并不唯一,故引理1的满类秩条件2)中ii)不成立.所以系统(A)不是结构可观的.由定义1可知,若系统(A)为结构不可观测的,则系统(A C)即为不可观测的.进一步,由文献[24]可知系统结构可观测的状态数目相应于系统二分图的左匹配节点数目.故,系统(4)和(5)不是完全可观测的,可观测的状态数目最大为7.又因为二分图的最大匹配一般不具有唯一性.所以,具体的这7个状态并不唯一. 证毕.

上述定理1不仅回答了静基座惯性导航系统是否可观测的问题,并且给出了可观测状态的数目.下面作为例子,对静基座INS进一步确定哪些状态是可观测的,哪些状态是不可观测的.

例3静基座INS可观测状态确定.对于惯性导航系统(4)和(5),其系统图3对应的二分图为图4,这个二分图中,左边节点1,2,···,10分别对应系统状态X的分量δv1,δv2,···,ε3.右边节点由观测节点和复制左边状态节点得到.由定理1可知,静基座惯性导航系统的最大可观测状态数目为7,相应于二分图4中最大匹配的左匹配节点.而这个二分图的最大匹配并不唯一,所以可观测的状态也不唯一.下面分析去掉3个状态时,二分图4中的最大匹配情形.为了简单起见,用数字代替原来系统中的状态分量.去掉{6,7,8},相应的最大匹配数为7,最大匹配为(9,4),(4,1),(1,y1),(10,5),(5,3),(3,2),(2,y2),此时可观测状态为δv1,δv2,ϕ1,ϕ2,ϕ3,ε2,ε3;去掉{6,8,9},相应的最大匹配数为7,最大匹配为(7,2),(2,y2),(10,5),(5,3),(3,4),(4,1),(1,y1),此时可观测状态为δv1,δv2,ϕ1,ϕ2,ϕ3,∇2,ε3;去掉{6,8,10},相应的最大匹配数为7,最大匹配为(9,4),(4,1),(1,y1),(5,3),(3,5),(7,2),(2,y2)或者(5,3),(3,5),(9,4),(6,1),(1,y1),(7,2),(2,y2),此时可观测状态为δv1,δv2,ϕ1,ϕ2,ϕ3,∇2,ε2或者δv1,δv2,ϕ1,ϕ3,∇1,∇2,ε2.去掉{5,6,7},相应的最大匹配数为6,最大匹配为(9,4),(4,1),(1,y1),(8,3),(3,2),(2,y2);去掉{5,6,9},相应的最大匹配数为6,最大匹配为(8,3),(3,4),(4,1),(1,y1),(7,2),(2,y2);去掉{5,6,10},相应的最大匹配数为6,最大匹配为(9,4),(4,1),(1,y1),(8,3),(3,2),(2,y2)或者(8,3),(3,4),(4,1),(1,y1),(7,2),(2,y2);去掉{4,7,8}或者{4,8,9},相应的最大匹配数为6,最大匹配为(6,1),(1,y1),(10,5),(5,3),(3,2),(2,y2);去掉{4,8,10},相应的最大匹配数为6,最大匹配为(6,1),(1,y1),(3,5),(5,3),(7,2),(2,y2).去掉{4,5,7},{4,5,9}或者{4,5,10}相应的最大匹配数为5,最大匹配为(6,1),(1,y1),(8,3),(3,2),(2,y2).当φ=时,相应的最大匹配数为6,最大匹配为(9,4),(4,1),(1,y1),(8,3),(3,2),(2,y2)或 者(6,1),(1,y1),(9,4),(4,3),(3,2),(2,y2).此时系统只有6个可观测的状态分量,分别为δv1,δv2,ϕ1,ϕ2,ε1,ε2或者δv1,δv2,ϕ1,ϕ2,∇1,ε2.

从这个例子可以看出,利用图论来研究INS的可观测性和可观测状态,可以得到与文献[2,7]中利用Cramer’s法则研究可观测度和奇异值判断可观测性相同的结论.

3.2 动基座INS的可观测性

这一小节讨论平台式INS在动基座下的可观测性和可观测状态的确定.为了与静基座时INS的误差模型相统一,这里使用相同的参数变量.在东-北-天坐标系下,删除位置误差状态变量及垂直通道的误差状态变量,假定加速度计误差为常值偏置,陀螺仪误差为常值漂移,并将∇1,∇2及ε1,ε2,ε3扩充为状态变量,则平台式INS在动基座下的对准误差模型可以表示为[1,6]

这里XXX=[δv1δv2ϕ1ϕ2ϕ3∇1∇2ε1ε2ε3]T为状态变量,系统矩阵

为时变的,其中0,I为适当维数的零矩阵和单位矩阵;块矩阵和分别为

的形式,其中fE,fN,fD分别是平台式惯导系统加速度计敏感到的比力在东向、北向、天向的分量,它们随时间变化.

为了研究动基座INS的可观测性,与文献[1]和文献[7]一样,假设对准过程中基座的运动方式为线运动,其可分为5个定常的时间段,具体分法见例4.在第j个时间段,INS误差方程可表示为

其中:矩阵Aj中除了块矩阵F(t)外,其它块矩阵都相同.记不同阶段的F(t)为

在基座的机动过程中,所有时间段都采用相同的测量分量,因此测量矩阵在整个对准过程中是不变的,仍然为方程(5).每个时间段中系统矩阵A都含有纬度参数,与静基座时INS情形相同,此处亦可利用图论来避免数值分析时具体的纬度值.为了给出连续PWCS的可观测性的图论特征,本文对一般的线性时不变系统(1)的动态图进行扩展.

定义4定义线性连续分段定常结构系统(2)的时间跨度n的动态图为

其中:k=1,2,···,r表示不同的阶段,

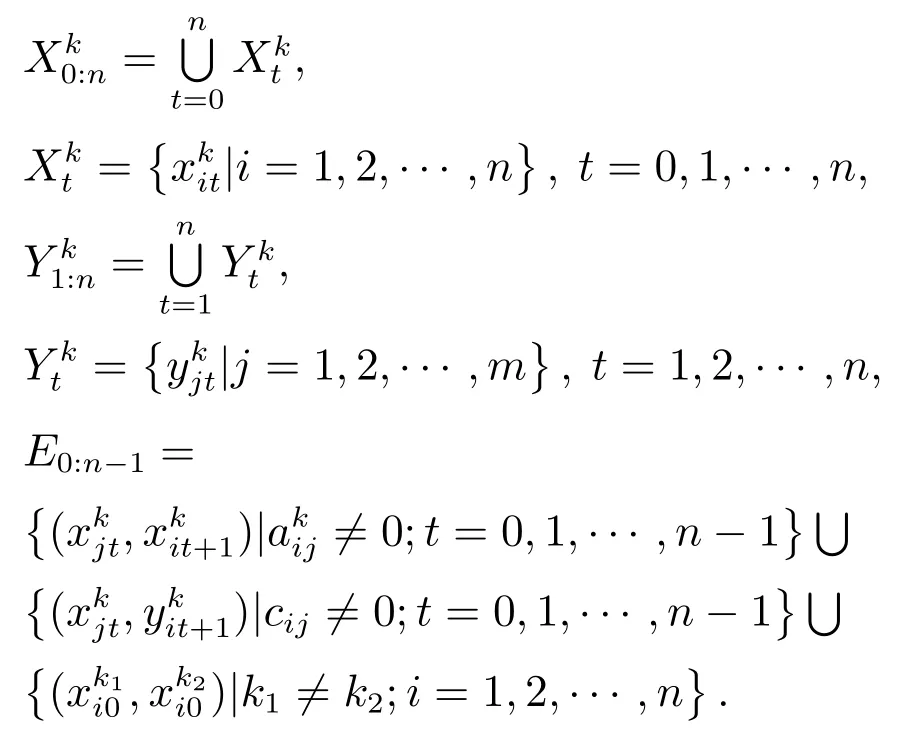
下面这个引理给出分段线性定常系统的系统矩阵为结构化矩阵时,系统结构可观的图论条件.

引理5假设具有r阶段的线性连续分段定常系统(2)满足null(Qj)⊆null(Aj),1 ≥j ≥r,当系统矩阵为结构化矩阵时,这个系统为结构可观测的充分必要条件是动态图G0:n中存在一个自到的n-Menger-type linking.

证必要性.因为线性连续分段定常系统(2)满足null(Qj)⊆null(Aj),1≥j ≥r,所以根据引理4可知:null(Q(r))=null(Qs(r)), rank(Q(r))=rank(Qs(r))成立[1].当系统矩阵为结构化矩阵时,如果存在一组参数使得矩阵Qs(r)为列满秩的,根据定义1可知,这个分段定常系统为结构可观测的.根据引理2和结构化矩阵的运算可知,任意结构矩阵Ak中的非零元素对应于矩阵A的有向图存在自状态节点xj到状态节点xi的长度为k的链接.这里,用归纳法进行说明.当k=1时,由邻接矩阵的定义可知,结论显然成立.假设k=l时,上述结论成立,下面说明k=l+1时亦成立.由矩阵的乘法可知,Al+1的非零元素可以表示为矩阵A的第i行元素与矩阵Al的第j列元素乘积之和,即若,则至少存在某个h使得,即有0和.因而从状态xj到xh存在长度为l的链接,从状态xh到xi存在一条边.因此,存在自状态节点xj到状态节点xi的长度为l+1的链接.同理可以证明,矩阵CAl中的非零元素dij表示自状态节点xj到输出节点yi的长度为l+1的链接.当线性连续分段定常系统(2)为结构可观测时,矩阵Qs(r)中一定存在n个不同行不同列的元素为非零.根据上述原因可知,这n个非零元素等价于动态图G0:n中存在一个自到的链接数为n的Menger-type linking.即在结构化意义下,这个系统为结构可观测时,G0:n存在一个自到的n-Mengertype linking.

充分性.如果动态图G0:n中存在一个自到的链接数为n的Menger-type linking,则由文献[23]和引理3可知,此时广义二分图中最大匹配的数目为n.即存在一组参数使得矩阵Qs(r)为列满秩的,由结构可观测性的定义可知,这个分段定常系统为结构可观测的. 证毕.

为了进一步分析的需要,这里引入一个广义二分图.其由不同阶段的二分图组成,这个广义二分图的最大匹配为不同阶段二分图匹配的并集(不同阶段具有相同的左右顶点的匹配为同一匹配).下面给出动基座时的主要结论:

定理2动基座下惯性导航系统(5)和(6)是不完全可观测的;其可观测的状态的最大数目等于动态图G0:10中自初始阶段的状态顶点到所有输出节点的最大Menger-type linking数目;相应的可观测状态为动态图中最大Menger-type linking含有的初始状态.

证动基座下惯性导航系统满足引理4中的条件,所以可以通过研究PWCS的可观测性来得到原来线性时变系统的可观测性.由引理2可知,结构矩阵Qs(r)的非零元素相应于系统图中的链接,从而可以用动态图来刻画.根据引理5可知,若动态图G0:10中最大Menger-type linking的数目为10时,惯性导航系统为结构可观测;并由其证明过程知,其可观测的状态的最大数目等于动态图G0:10中自初始阶段的状态顶点到所有输出节点的最大Menger-type linking数目.但易知G0:10中最大Menger-type linking的数目小于10.事实上,通过对广义二分图的分析,容易得到其Menger-type linking的数目为9,也就是说在动基座条件下,惯性导航系统的可观测状态数目最大为9,故惯性导航系统不是结构可观测的,根据定义1可知,这个系统亦不是完全可观测的.又由PWCS理论可知,相应的可观测状态可以由动态图G0:10中最大Menger-type linking含有的初始状态来得到. 证毕.

注3定理2在动基座下的可观测性分析结果与文献[9,30-31]中的结论不同.该文是针对未考虑GPS装置辅助作用时的平台式惯性导航系统模型进行分析的,文献[9,31]考虑的是捷联式惯性导航系统模型,故不同模型下可观测性的分析结果不同.另外,文献[10,30]引入的GPS装置可以提供额外的位置信息,从状态方程和测量方程的表达角度来讨论,引入GPS装置可以增强系统的可观测性.

上述定理利用动态图的Menger-type linking得到动基座惯性导航系统是不可观测的.对于低阶或分段数较少时,绘制和分析动态图相对容易,但当分段数和系统维数较高时,利用动态图分析相对困难.下面,利用广义二分图来具体分析动基座惯性导航系统在不同阶段的可观测性与可观测状态.

例4动基座INS可观测状态确定.动基座对准过程中,水平机动能力能够用分段定常水平加速度来代替.可以验证机动过程的存在能够明显的影响惯导系统的可观测程度.一般用PWCS来分析动基座平台式惯导系统.分段情况分别为:1)匀速直线运动(fE=fN=0,fD=g);2)具有北向加速度的直线运动(fE=0,fN0,fD=g);3)具有东向加速度的直线运动(fE0,fN=0,fD=g);4)具有水平加速度的直线运动(fE0,fN0,fD=g);5)上、下加速运动(fE=fN=0,fD0).

由于分析方法相似,这里仅对前两个阶段给出图形和分析过程,后面阶段可以仿照于此利用广义二分图给出相应结论.对于具有北向加速度的直线运动时的情形,其系统图为图5,在原来图3的基础上增加一条自节点5到节点1的有向边.这个图对应的二分图为图6,这个二分图中,左边节点1,2,···,10分别对应系统状态X的分量δv1,δv2,···,ε3.右边的圆形节点是对左边节点的复制,三角节点表示测量传感器.

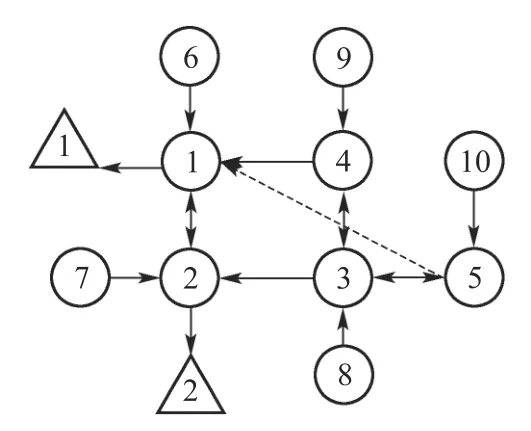
图5 具有北向加速度的平直运动的系统图Fig.5 System graph associated with the straight line motion under the north acceleration

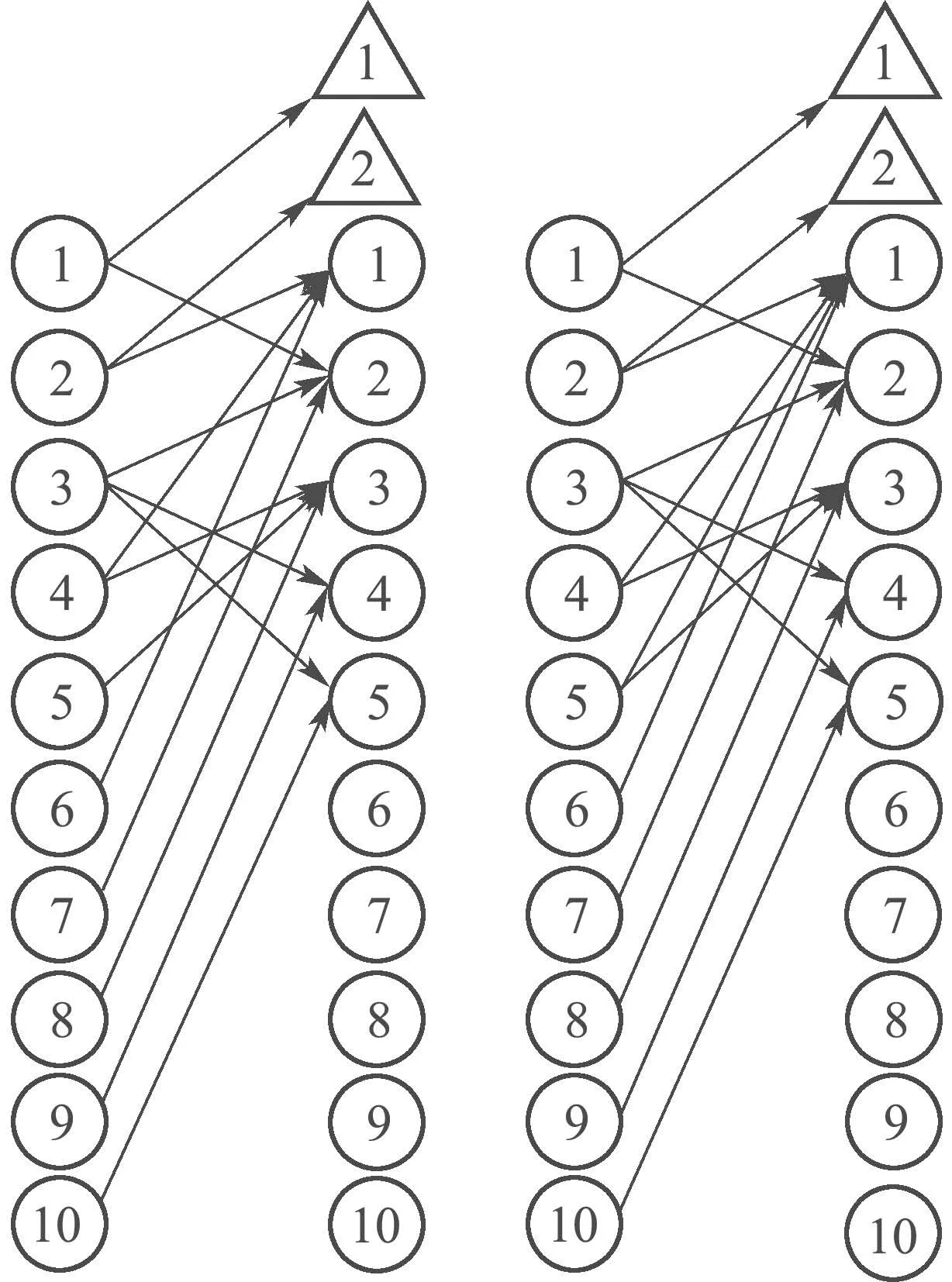
图6 匀速和具有北向加速度的平直运动的广义二分图Fig.6 Generalized bipartite graph associated with the straight line motion under the uniform velocity and north acceleration

因为此二分图的右边匹配节点最多为7,可知最大匹配数为7,除了阶段1(静基座)的3个最大匹配外,还存在最大匹配(10,5),(5,1),(1,y1),(9,4),(4,3),(3,2),(2,y2),其相应的不可观测状态为{6,7,8}.对于具有东向加速度的直线运动时的情形,除了阶段1(静基座)的3个最大匹配外,还存在最大匹配(10,5),(5,2),(2,y2),(8,3),(3,4),(4,1),(1,y1),其相应的不可观测状态为{6,7,9}.其它2个阶段可以仿照上述分析方法得到相应的最大匹配.由上述最大匹配可知,无论从哪一阶段开始,此时的最大可观测状态数都为7,基座通过运动可以增加可观测的状态,但是无论上述5个阶段怎样运动,惯性导航系统都不是完全可观测的.

4 结论

文中利用组合图论中二分图的匹配理论和Mengertype linking知识建立了平台式惯性导航系统的可观测性分析以及可观测状态确定的基本框架.针对静基座和动基座的情况,分别给出其可观测性的图论特征以及可观测状态的确定过程.这里的方法是结构化理论中常用到的,对于可以建模为线性系统的GPS/INS组合导航系统的可观测性分析,也可以利用文中的方法来处理.作者将进一步利用图论来研究组合导航系统和运动学模型时导航系统的结构可观测性问题,关于具有强非线性的捷联式惯性导航系统的结构可观测性分析,需要对图论描述法和非线性系统之间的关系深入研究后方能展开.