基于双目融合的无参考立体图像质量评价*

王 杨，向秀梅，卢 嘉，郁振鑫

(1.河北工业大学电子信息工程学院,天津 300401;2.河北工业大学天津市电子材料与器件重点实验室,天津 300401)

1 引言

随着立体图像相关技术的发展，准确地评价立体图像在采集、存储、压缩、传输等过程中的失真程度逐渐成为研究热点[1]。立体图像质量的客观评价以其评价方式便捷、结果客观可靠等优势而被普遍应用。根据评价过程参考图像的信息量将客观评价方法分为3种：全参考型、半参考型和无参考型[2]，其中无参考型评价方法无需参考图像信息，更为便捷和实用。

Figure 1 Overall framework of the non-reference stereo image quality evaluation method图1 无参考立体图像质量评价方法的整体框架

由于立体图像由左、右视点图像构成，包含深度信息和视差信息，不能将单目图像评价方法直接用于立体图像质量评价[3]。Chen等人[4]利用从立体图像提取的二维和三维特征来评估立体感知质量。马允等人[5]提取梯度幅值、拉普拉斯特征、空域自然场景统计特征训练无参考立体图像评价模型。Zhang等人[6]在卷积神经网络的基础上，通过单通道和三通道提取图像特征来评价立体图像质量。Liu等人[7]通过合成三维视觉显著图来实现不同区域的权重分配，将更高的权重分配给更重要的感知区域。Lin等人[8]提取相位一致性测量中的局部相位和局部幅度，并提出将其作为主要特征的立体图像质量评估框架。Ma等人[9]在梯度域中，通过联合考虑人类视觉系统的对比灵敏度和邻域梯度信息来生成修改的梯度幅度图，结合空间和梯度域的质量以提高立体图像的整体质量。Yao等人[10]利用双变量自然场景统计模型，分别从双眼融合、双眼竞争和双眼抑制区域提取特征来捕获图像质量。Zhou等人[11]提出了一种左、右视图子网之间包含多层网络交互体系结构的无参考立体图像质量评价方法。

基于上述提取立体图像特征训练评价模型的思想，以及三维视觉显著性由二维视觉显著性和深度信息构成的启发[12]，本文在双目特性的基础上融合左、右视点图像和视差信息，以此来获取深度信息，并结合Gabor小波变换图像和灰度共生矩阵反映出二维视觉显著性部分特征这一特点，提取深度信息的显著性特征，即三维显著性特征。通过建立左、右视点图像和合成图像特征与图像质量间的回归关系，提出一种基于双目融合的无参考立体图像质量评价方法。该方法评价对称失真和非对称失真类型立体图像均具有较高准确性，目前尚未见报道。

2 立体图像质量评价模型

本文所提出的无参考立体图像质量评价方法如图1所示，图中DMOS(Difference Mean Opinion Score)为差异平均主观得分，SVR(Support Vector Regression)为支持向量回归，Q(Quality)表示所得评价值。首先利用拉普拉斯金字塔完成左、右视点图像的逐层分解，采用每层图像区域能量或平均梯度确定该层融合系数，在双目加权模型基础上构建合成图(Cyclopean Image)；然后对左、右视图和合成图像进行二维显著性特征提取；最后将特征向量和主观评价值输入到支持向量回归SVR模型中进行训练并预测立体图像评价值。

2.1 构建合成图像

合成图像的构建需要先将参与合成的左、右视点图像逐层分解，本文采用拉普拉斯金字塔分解，分解步骤如下所示：

步骤1利用高斯核分别将参加融合的左、右视点图像IL、IR分解为高斯金字塔图像序列；

步骤2将每层图像与内插放大的上一层图像作差，可得该层的拉普拉斯金字塔分解图像；

步骤3由下至上重复内插放大、作差过程，形成左、右视点图像的拉普拉斯金字塔序列，分别为{IL0,IL1,…，ILn}、{IR0,IR1,…，IRn}，底层图像为IL0、IR0，顶层图像为ILn、IRn。

合成图像包含了左、右视点图像和视差图像所包含的信息，可用双目加权模型[13]构建合成图像：

CI(x,y)=ωL(x,y)×IL(x,y)+

ωR(x+d,y)×IR(x+d,y)

(1)

其中，IL和IR分别为左、右视点图像，d为视差信息。ωL、ωR分别为左、右视点图像的融合系数，因图像平均梯度和区域能量均包含图像局部纹理信息，这里采用平均梯度和区域能量来逐层分析融合权重。

Figure 2 Cyclopean images of distorted stereo image pairs图2 失真立体图像对的合成图像

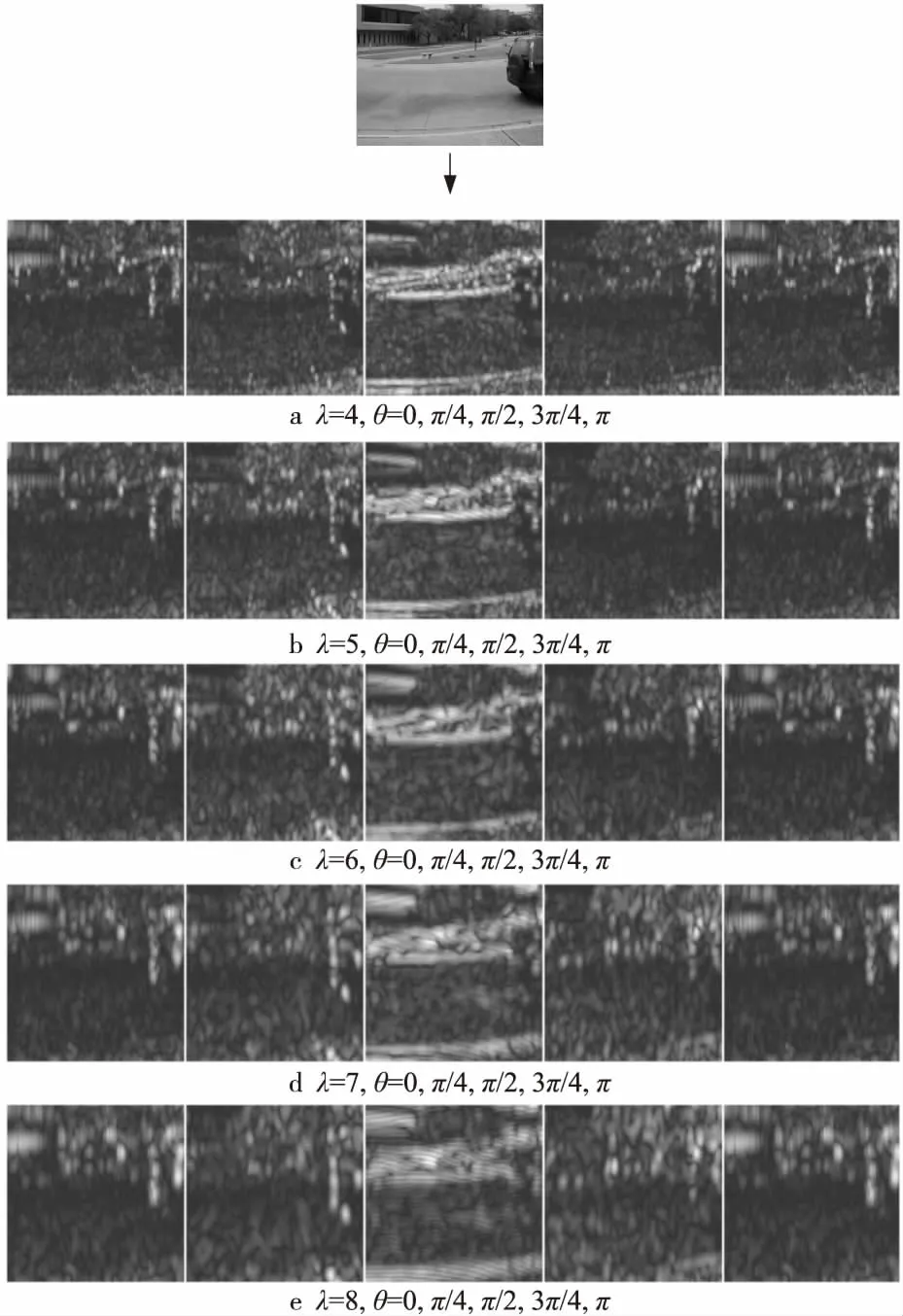
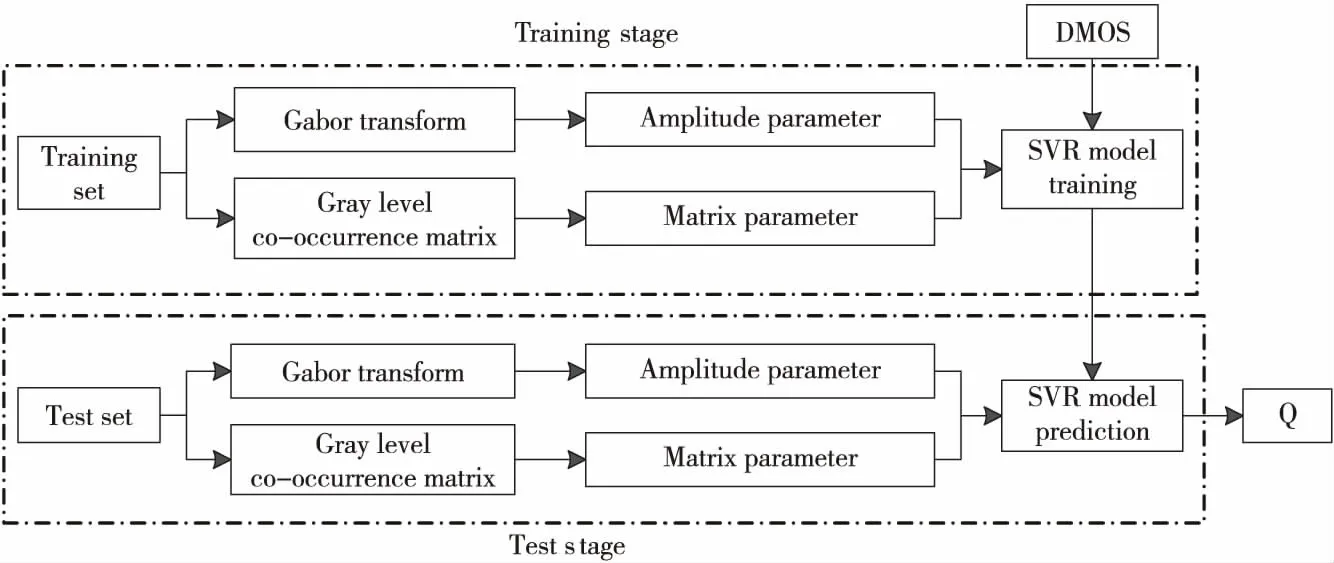
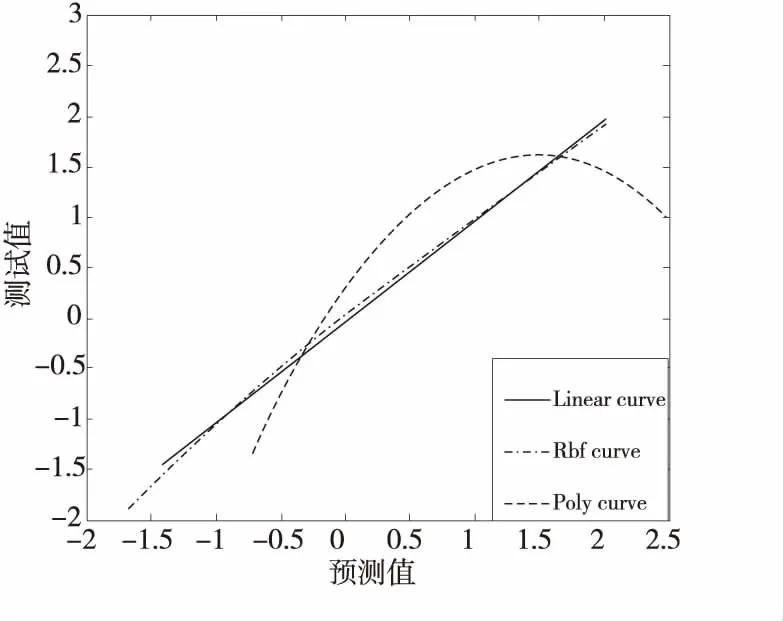
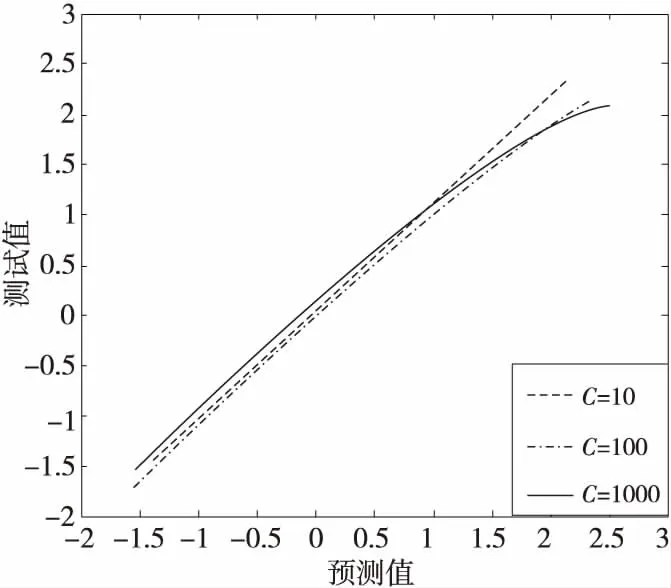
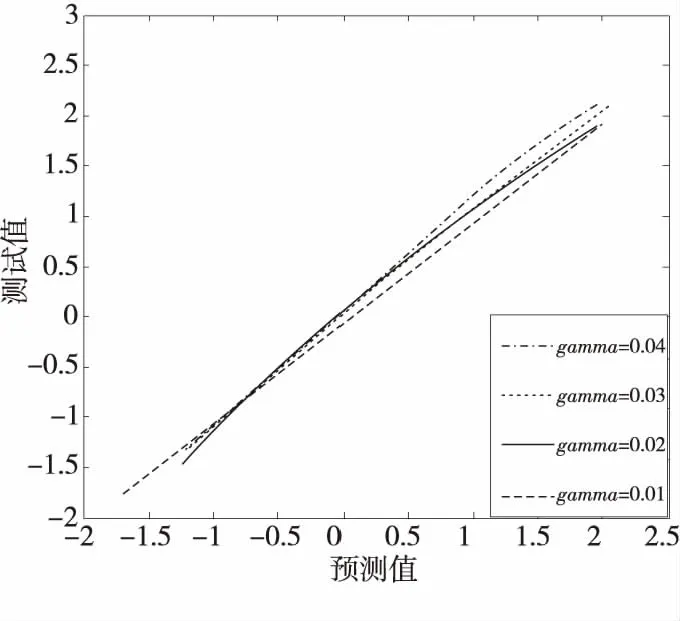
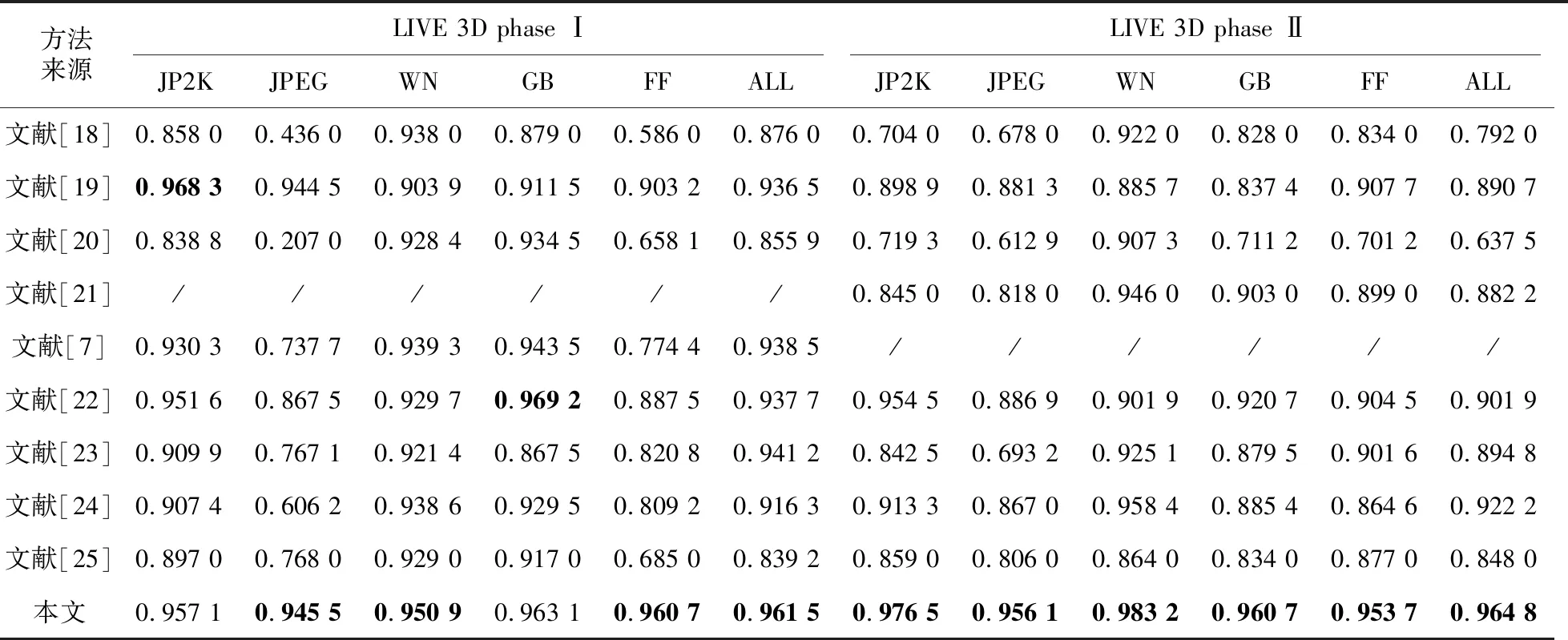
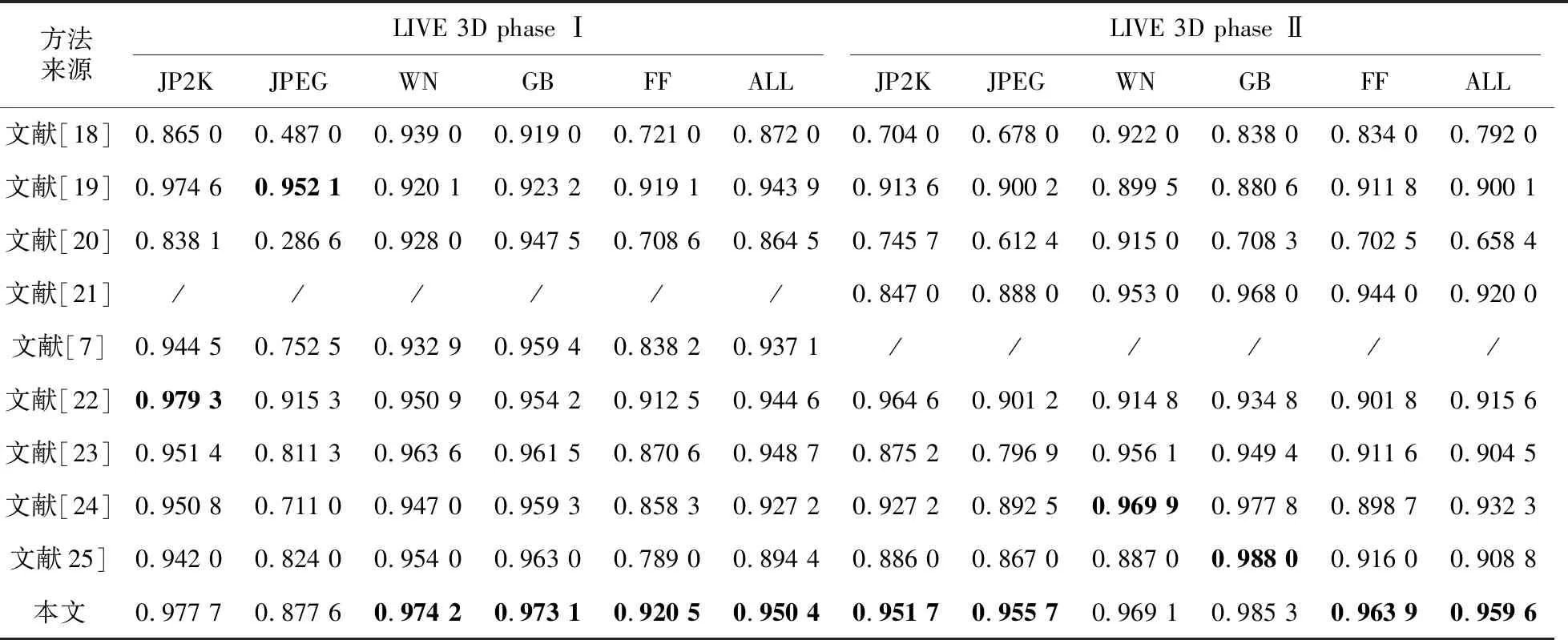
在双目加权模型上由下至上将左、右视点图像的拉普拉斯金字塔序列逐层融合，其中顶层图像ILn、IRn的融合系数采用平均梯度来分析，中间层图像ILm、IRm(0

(2)

(3)

其中，GRn为IRn的平均梯度，ERm(i,j)为IRm的区域能量，M、N为左、右视点图像大小，ΔIx、ΔIy分别为像素f(x,y)在x、y方向的一阶差分。

同理可得顶层图像ILn的区域平均梯度GLn和中间层图像ILm的区域能量ELm(i,j)，则顶层图像和中间层图像的融合系数为：

(4)

(5)

如图2所示，样本来自图像库LIVE 3D phase Ⅰ[14],分别为立体图像在高斯模糊、瑞利衰落、JP2K压缩、JPEG压缩、白噪声失真下的合成图像。

2.2 特征提取

二维视觉显著性是定位人眼感兴趣区域的重要机制，而人眼存在着纹理敏感性，纹理敏感性会对有着明显纹理变化的区域分配更多的注意力，本文采用Gabor小波变换和灰度相关矩阵抽取局部纹理特征。与二维图像相比，立体图像携带的深度信息也影响着视觉感知。将深度信息与二维显著性特征检测方法相结合，建立提取三维显著性特征的立体图像质量评价模型。

2.2.1 Gabor小波特征

Gabor滤波器的频率和方向与人眼视觉系统存在相似性[15]，且可以提取图像不同方向的纹理信息，能够提供良好的方向选择和尺度选择，因此本文采用Gabor滤波作为第一步特征提取方法。二维离散Gabor小波变换过程可用式(6)表示:

(6)

x′=xcosθ+ysinθ

(7)

y′=-xsinθ+ycosθ

(8)

其中，(x,y)为图像中的像素坐标点，λ表示波长，也代表Gabor滤波器的尺度，θ表示滤波器的方向，φ为相位偏移，σ为标准差；γ表示空间纵横比，决定了滤波器的形状，通常取γ=0.5。本文将滤波核中平等条带的方向θ选取为0,π/4,π/2,3π/4,π,Gabor核函数中余弦函数的波长参数λ=4,5,6,7,8,即生成5种方向5种尺度的滤波器组，将图像与滤波器组卷积可得变换图像，如图3所示。

Figure 3 5-scale,5-direction Gabor wavelet transform image图3 5尺度、5方向的Gabor小波变换图像

选取不同的尺度和方向，利用所得的不同Gabor滤波器对图像进行变换，分别提取变换后图像幅度的均值和方差特征,可得2×a×b维的特征向量：

Figure 4 Stereo image quality evaluation model图4 立体图像质量评价模型A=[μ0，0,σ0，0,μ0，1,σ0，1,…,μa-1,b-1,σa-1,b-1]

(9)

本文取5种方向5种尺度，θ=0,π/4,π/2,3π/4,π，λ=4,5,6,7,8，即a=5，b=5。将左、右视点图像和合成图像进行幅度参数提取，分别用AL、AR和AC表示。

2.2.2 灰度共生矩阵特征

图像的灰度相关特性表现为某距离的2像素之间存在某灰度关系[16]，因而利用灰度共生矩阵描述图像的灰度相关特性。本文通过计算灰度共生矩阵的4个最常用的特征值，来表示图像的部分纹理特征。

(10)

(11)

(12)

(13)

式(10)～式(13)分别为灰度共生矩阵的对比度、熵、能量、逆差分矩的计算公式。其中，pθ(i,j)为图像在方向θ上计算的L阶灰度共生矩阵，本文将方向θ分别设置为水平方向、竖直方向、主对角线和副对角线方向，可得到4个方向的特征参数：

B=[G1,0°,G1,45°,G1,90°,G1,135°,…,

G4,0°,G4,45°,G4,90°,G4,135°]

(14)

通过式(14)提取左、右视点图像和合成图像的灰度共生矩阵特征，分别表示为BL、BR和BC。

2.3 基于双目融合的无参考立体图像质量评价模型

对左、右视点图像和合成图分别进行Gabor小波变换幅度特征和灰度共生矩阵特征提取，右视点图像表示为GR=[AR,BR]，左视点图像表示为GL=[AL,BL]，合成图像表示为GC=[AC,BC]。将每对立体图像的特征参数记为G=[GR,GL,GC]，其中共提取的特征数为198。

如图4所示，模型分为训练部分和测试部分。训练部分将提取的特征集与主观评价值作为SVR模型的输入，进行模型的训练，得到特征值与主观评价值之间的映射。模型在Python3.7环境下进行训练和预测。测试部分根据特征值与主观评价值之间的映射，将部分立体图像的特征值输入到训练模型中，得到预测的评价值。

3 实验与结果分析

3.1 样本集划分

本文选取了 LIVE 3D phase Ⅰ和 LIVE 3D phase Ⅱ立体图像数据库进行测试，LIVE 3D phase Ⅰ中共有365幅失真立体图像和20幅参考图像，其中失真类型包含高斯模糊、JEPG 压缩、高斯白噪声、JP2K压缩和快速衰退。LIVE 3D phase Ⅱ中共有360幅失真立体图像和8幅参考图像[17]，其中失真类型包含对称失真和非对称失真2大类。将所有样本随机划分为训练和测试2个部分，其中80%用于训练，20%用于测试。

3.2 参数设定

本文采用的核函数分别为Rbf，Linear和Poly,如图5所示，横坐标为预测值，纵坐标为测试值，采用Rbf核函数时，模型的预测曲线最为准确，此曲线上的预测值几乎等同于测试值，故本文选用Rbf核函数对样本集进行训练。C为惩罚因子，分别设置惩罚因子为10,100,1 000，从图6可以看出，随着惩罚因子的增大，预测值逐渐偏离测试值。而Rbf 核函数的核系数gamma的改变对训练模型影响较小，如图7所示，随着gamma的减小，预测值逐渐等同于测试值，预测结果在gamma=0.01时最为准确。因此，将训练模型的惩罚因子和核系数分别设置为10和0.01。

Figure 5 Prediction curves with different kernel functions图5 使用不同核函数时的预测曲线

Figure 6 Prediction curves with different penalty factors图6 不同惩罚因子的预测曲线

Figure 7 Prediction curves with different kernel coefficients图7 不同核系数的预测曲线

3.3 数据库上的实验结果

本文采用Spearman等级相关系数SROCC(Spearman Rank Order Correlation Coefficient)和Pearson线性相关系数PLCC(Pearson Linear Correlation Coefficient)客观分析所提评价模型的相关性，SROCC和PLCC值越接近1，模型预测值与主观评价值的相关性越高。

表1分别比较了SSIM[18]、文献[7,19-25]和本文方法在LIVE 3D phase Ⅰ、LIVE 3D phase Ⅱ立体图像数据库上的SROCC指标，表2分别比较了它们的PLCC指标。其中文献[18]的SSIM为平面图像质量评价方法，其余文献均为无参考立体图像质量评价方法。

表格中5种失真类型分别为高斯模糊、瑞利快衰退、JP2K压缩、白噪声和JPEG压缩，对每种失真类型的最佳评价方法采用加粗标注。由表1和表2中数据可知，在LIVE 3D phase Ⅰ 数据库上，本文所提方法的SROCC指标相比于其它对比方法分别提高了9.8,2.7,12.3,2.4,2.5,2.2,4.7,12.7个百分点，PLCC指标分别提高了9.0,0.7,10.0,1.4,0.6,0.2,2.4,5.9个百分点。在LIVE 3D phase Ⅱ 数据库上，本文所提方法的SROCC指标分别提高了21.8,8.3,51.3,8.6,7.0,7.8,4.4,12.1个百分点，PLCC指标分别提高了21.1,6.6,45.7,4.1,4.8,6.1,2.8,5.3个百分点。数据分析表明，本文方法对于对称失真和非对称失真图像的评价均具有较高一致性，总体优于其他对比方法。

Table 1 SROCC coefficients on the databases表1 数据库上的SROCC系数

Table 2 PLCC coefficients on the databases表2 数据库上的PLCC系数

4 结束语

本文提出了一种结合图像融合的无参考立体图像质量评价方法。双目加权模型能够模拟视觉感知的处理过程，为得到立体图像对的深度信息，引入双目加权模型分别对左、右视点图像进行分解、融合、重构，并结合双目感知和二维显著性特征，提取合成图像的局部频域、能量、熵、对比度等特征作为三维显著性特征。结果表明，该方法对于对称失真和非对称失真立体图像的评价均与主观评价值具有较高的相关性，可以作为一种评价立体图像质量的新思路。