基于比特估计的RFID标签数量估计算法*
杨 帆,任守纲,徐焕良,孙元昊,杨 星
(1.江苏师范大学数学与统计学院,江苏 徐州 221116;2.南京农业大学工学院,江苏 南京 210031; 3.南京农业大学信息科学技术学院,江苏 南京 210095)
1 引言
物联网是新一代信息技术的重要组成部分,也是信息化时代的重要发展阶段。无线射频识别RFID(Radio Frequency IDentification)作为物联网感知层关键技术之一,对物联网的发展起着至关重要的作用[1]。标签防碰撞算法主要用于解决RFID系统中多标签碰撞问题[2 - 6],而准确估计标签数量作为提高标签防碰撞算法效率的重要环节,吸引了大量研究人员的关注。目前,标签数量估计算法[7 - 22]主要分为2大类,分别为基于帧时隙的标签估计算法[7 - 18]和基于比特估计的标签估计算法[19 - 22]。
基于帧时隙的标签估计算法又分为2类:1类是固定系数或经验系数的估计算法,如Low Bound估计算法[9]、Schoute 估计算法[10]和基于空闲时隙估计算法[11]等。该类算法具有时间复杂度低的优点,但其估计误差较大。另1类是根据区间最优值搜索的估计算法,如Vgot算法[12]、贝叶斯算法[13,14]和最大后验概率估计算法[15,16]等。该类算法虽然具有较高的标签估计精度,但由于其在标签的取值范围内多次求极值,使得算法的计算复杂度高。
基于比特的标签估计算法也可分为2类:1类是基于比特时隙的估计算法[19,20],如ART(Average Run based Tag estimation)估计算法[20]。该类算法将单个时隙内的标签回复量设定为1个比特,即当前时隙有标签选择,则标签回复1,否则回复0,这大大降低了读写器和标签之间的通信开销,但其仍然需要较多时隙来完成标签数量的估计。另1类是基于比特字符串的估计算法[21,22],如OBTT(Optimal Binary Tracking Tree protocol)算法[22]。该类算法以比特字符串代替时隙,并设定标签从读写器发布的比特字符串中任意选择1个比特位设定为1,其余位设定为0,然后返回产生的比特字符串。利用曼彻斯特编码技术,读写器聚合接收到的比特字符串,并统计聚合后比特字符串中未被标签选择的比特位个数,进而计算出比特字符串中的空闲比特率IBR(Idle Bit Rate),若有IBR≠0,则进行标签数量估计。
无论是基于帧时隙的标签估计还是基于比特的标签估计,从统计意义上看每个帧时隙状态(空闲、成功和碰撞)或字符串的比特位状态(选择和未选择)都符合二项分布定理。对于文献[22]中提出的标签估计算法,尽管在IBR值较大时具有较高的准确性,但在IBR近似为0时,面临如下2个问题:
(1)根据二项分布理论,对于具有不同数量标签的2组标签群,当2者的标签实际数量都远大于用于标签估计的比特字符串长度时,比特字符串的空闲比特率仍会出现IBR=1/S的情况,其中S为比特字符串的长度。此时,如何根据IBR的值精准估计这2组标签群内标签的实际数量?
(2)由于IBR的值与标签实际数量n和S的比值密切相关,在S/n→0的过程中,标签的估计误差会出现较大波动,那么是否存在1个非零且非1/S的IBR阈值TIBR(Threshold of Idle Bit Rate),当有IBR≥TIBR时,使得标签估计的误差率e(2.3节将给出定义)在任意标签实际数量下有e|TIBR,n≤e|1/S,n,且e值的波动较小。
通过对上述2点的分析,本文在文献[22]的基础上提出了基于比特估计的优化算法OBE(Optimization of Bit Estimation)。该算法通过引入TIBR取代S-1作为开启标签估计的判断条件,使得标签的估计误差大大降低。同时,通过分析不同TIBR在不同标签实际数量下的误差率和时隙消耗的均值和方差,寻找面向不同标签规模的最优TIBR。仿真结果显示,OBE算法相比现有的标签估计算法具有更高的精度,且在不同规模的标签群上具有更加稳定的标签估计性能。
综上所述,本文的贡献总结如下:
(1)提出了基于比特估计的优化算法。该算法通过引入TIBR解决了文献[22]中未考虑在IBR近似为0时的问题,在不同稠密度的标签环境中进行仿真实验,得出了独立于标签稠密度的最优TIBR值。最终仿真结果显示,OBE算法具有更高的标签估计准确度。
(2)利用二项分布和容斥原理等理论,对OBE算法中用于标签估计的时隙消耗进行了分析,并给出了OBE算法时隙消耗的数学表达式。
2 OBE算法
相比基于时隙的标签估计算法,基于比特字符串的估计算法利用曼彻斯特编码技术,通过在1个时隙内检测每个比特位的状态而不是在1个识别帧内检测时隙的状态来估计标签的数量。因此,基于比特字符串的估计算法可以使用较少的时隙开销完成对标签数量的估计。OBE算法分为2个阶段,分别是比特字符串长度调整和标签数量估计。表1给出了本文常用的数学符号及说明。
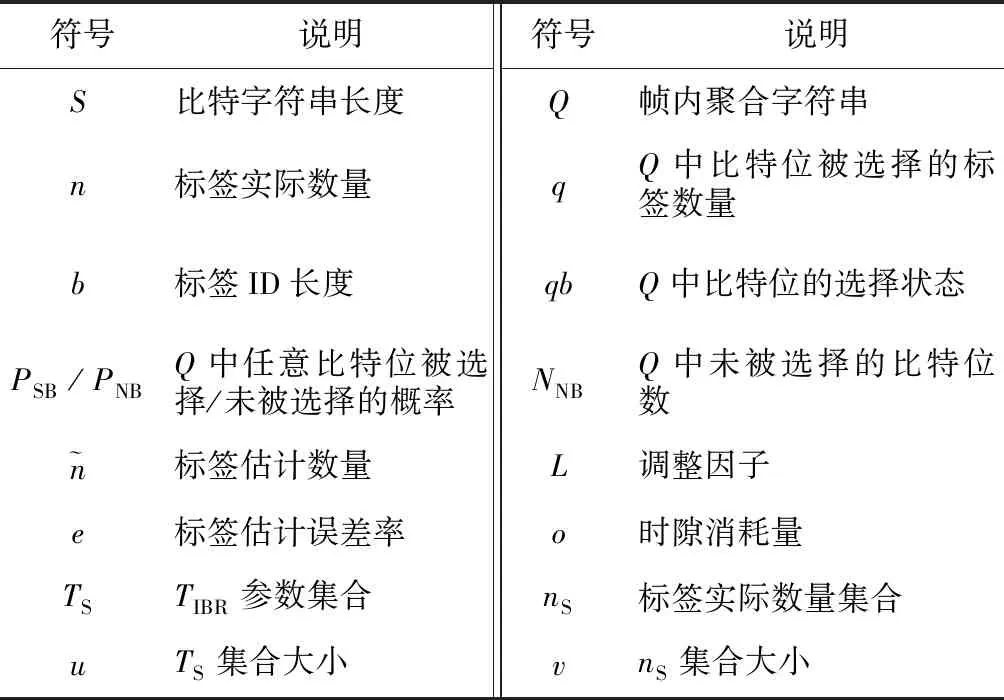
Table 1 Mathematic symbols表1 常用的数学符号
2.1 比特字符串长度调整
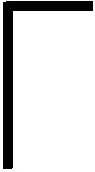
利用曼彻斯特编码技术,读写器分别合并1~L个时隙内标签回复的字符串,以获得该帧内聚合字符串Q={q0,q1,…,qS-1},其中qi={0,1,X},qi=0表示字符串的第i个比特位未被选择;qi=1表示第i个比特位只被1个标签选择,否则表示该比特位被多个标签选择。如果用qbi表示Q中第i个比特位的选择状况,则有:
(1)
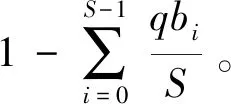
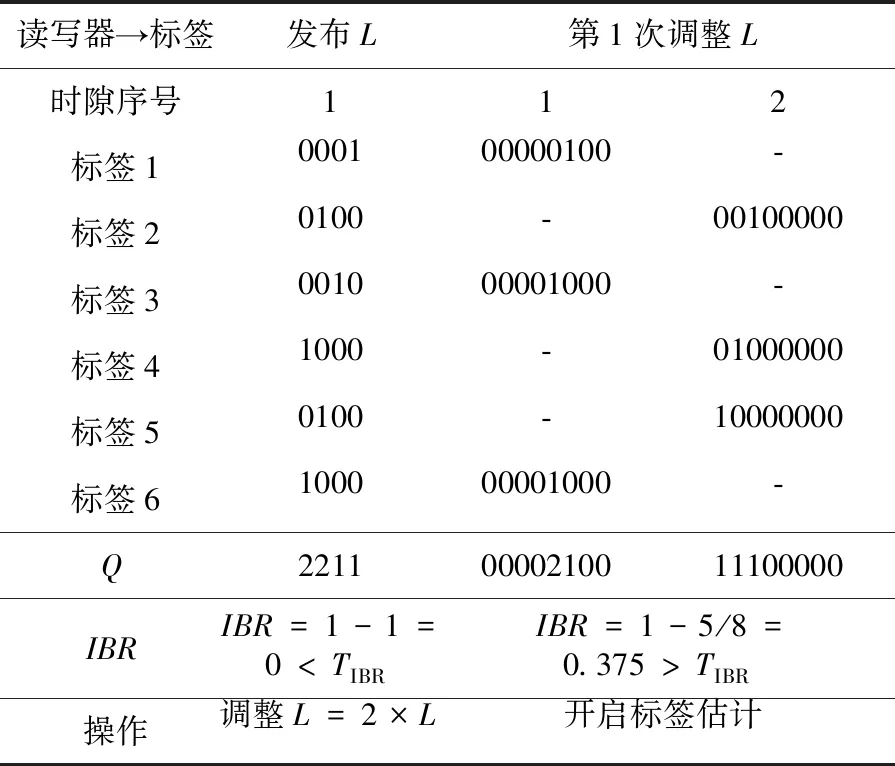
Table 2 Adjusting process of bit sequence length in OBE algorithm表 2 OBE算法比特字符串长度的调整过程
2.2 标签估计
对于Q中任意比特位被标签选择和未被选择的概率分别记为PSB和PNB,则有:
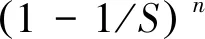
(2)
PSB(n,S)=1-PNB(n,S)
(3)
根据文献[3]可知,基于时隙的标签估计,在任意1个帧中出现空闲时隙的数量其均值满足:
E[I]=F×P(n,F)(0)
(4)
其中,I表示空闲时隙的数量,F表示帧长,P(n,F)(0)表示空闲时隙的概率。
对于Q中未被选择的比特位数NNB,结合式(2)和式(4)有:
(5)
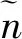
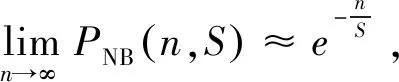
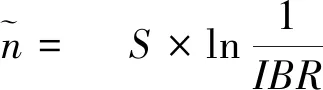
(6)
2.3 参数的选择
TIBR是OBE算法的关键参数,最优的TIBR取值不仅可以降低标签估计的误差率,还能够保证在不同规模的标签群上具有相对稳定的标签估计性能。
为了描述TIBT的取值对于误差估计准确性的影响,本文使用文献[9]中提到的归一化估计误差函数δ作为评判标准,其表示如下:
(7)
由于文献[23]给出了空闲率的最大上限值,本文以此为基础,设定TIBR的参数集TS={0.05,0.1,…,0.35,0.4},其集合大小u=8,标签实际数量的参数集nS={100,120,140,…,1 980,2 000},其集合大小v=96。同时,定义误差矩阵EM(Error Matrix)来观察不同TIBR和n对δ的影响,EM表示如下:
(8)
其中,evu为误差率,其值为:
evu=δ|TIBT=TS(u),n=nS(v)
(9)
利用OBE算法,以Matlab为仿真工具,在b=96的条件下,分别对不同TS和nS的取值组合进行仿真,每种组合迭代200次取均值得到其对应的e值和时隙消耗,仿真结果如图1所示。从图1中可发现,误差率e与标签实际数量n和TIBT均成反比关系,而时隙消耗数量o与标签实际数量n和TIBT成正比关系。
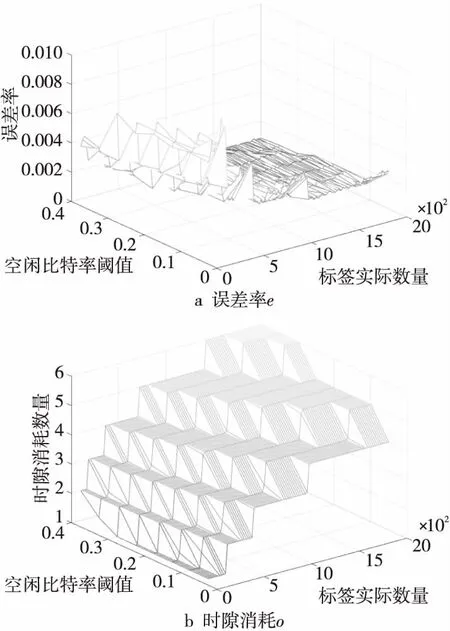
Figure 1 Error rate e and slot consumption o under different n and TIBT图1 不同组合下的误差率e和时隙消耗数量o
EM呈现了不同取值组合与误差率之间的关系,在相同的标签实际数量n下,较大的TIBR具有较小的误差率,但仍无法确定最优的TIBR取值。因此,本文引入误差率e的均值集合we={we1,we2,…,weu}和标准差集合σe={σe1,σe2,…,σeu},以及时隙消耗数量o的均值集合wo={wo1,wo2,…,wou}和标准差集合σo={σo1,σo2,…,σou},来分析不同TIBR值下标签估计的误差率及误差波动情况,以寻找最优TIBR值。该4类参数计算方法如式(10)和式(11)所示,结合图1中的数据集合,其计算结果如表3所示。
(10)
(11)
从表3中可清晰地看出,we与TIBT成反比关系,即TIBT越大,OBE算法的估计性能越好,这与前面分析的结果相同。在不同TIBT下,σe的取值出现上下浮动,当TIBR=0.35时,σe的值最小,即表明此时OBE算法受标签数量n的影响最小。wo与TIBT成正比关系,即TIBT越大,OBE算法所消耗的时隙数量越多。当TIBR=0.35时,σo的值最大,这表明OBE算法可以根据标签实际数量自动调整时隙消耗数量。综上考虑,本文设定最优的TIBT为0.35。
3 OBE算法性能分析
相比基于时隙的标签估计算法,OBE算法利用比特跟踪技术可减少因标签估计而产生的时隙数量,故本节主要分析标签估计所消耗的时隙数量。
假设T表示在标签实际数量为n的条件下第i次调整L时,Q中被选择比特位的个数,则有:
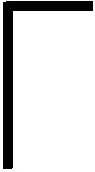
(12)
其中,Li=2i-1×L。
以Rx表示在标签实际数量为n的条件下第i次调整L时,Q中第x位未被选择的所有排列组合形式的集合,则其所有排列组合的数量为:
(13)
以Rx∩Ry表示在标签数量为n的条件下第i次调整L时,Q中第x位和第y位未被选择的所有排列组合形式,则有:
(14)
根据容斥原理,并结合式(12)和式(14),则对于Q中有T个比特位都被选择的所有排列组合数量为:
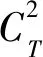
(15)
在标签实际数量为n的条件下第i次调整L的概率PA(i,n)为:
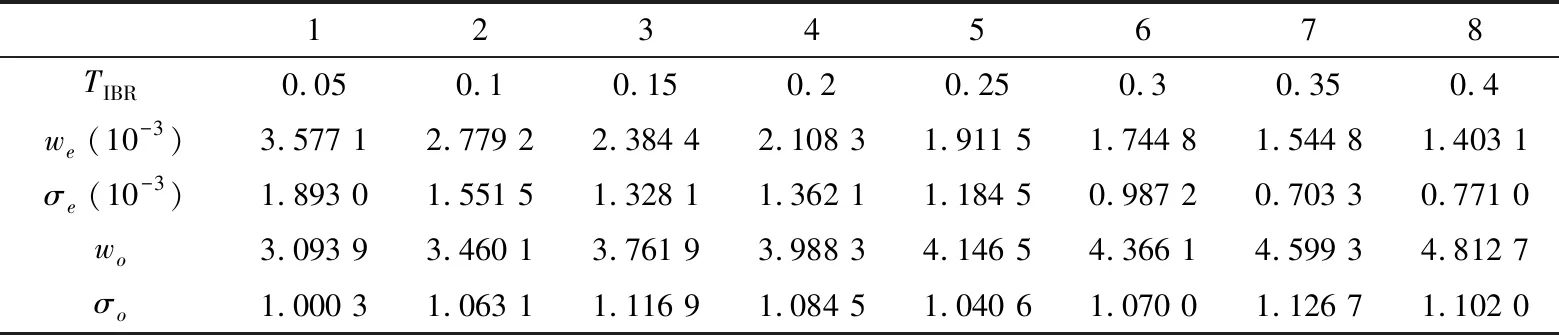
Table 3 Mean values and standard deviations of error rate and slot consumption under different TIBR表3 不同TIBR下的误差率和时隙消耗的平均值和方差

(16)
由于当n (17) 以PS(i,n)表示在标签实际数量为n的条件,第i-1次调整L后满足IBR≥TIBR的概率,则有: (18) 以H(i)表示第i次调整L需要的时隙数量,则有: (19) 因此,前i次标签估计消耗时隙的数量为: (20) 根据等式(17)、式(18)和式(20),则对n个标签估计所消耗的平均时隙A(n)为: (21) 本节利用计算机仿真实验验证所提出的估计算法的性能。在仿真实验中,假设该RFID系统仅有1个读写器,标签ID服从均匀分布,所有标签被读写器识别的过程中一直处于读写器的工作范围,且在整个识别过程中标签实际数量不会发生改变。同时,假定系统中的信号在信道传输和接收的过程中不存在误码问题且无捕获效应。标签数目n设定为50,55,60,…,2 000。每设置1次n,实验重复200次取平均值。 本节给出了在不同标签ID长度b下,OBTT算法和OBE算法的估计误差率随标签实际数量n的变化曲线图,如图2所示。从图2中可以很明显地看出,OBE算法的估计性能明显优于OBTT算法的,且基本不受标签ID长度和标签实际数量的影响。在b=64,n≤65和b=96,n≤95时,OBE算法和OBTT算法具有相同的估计误差,这是由于此时2者具有相同的IBR值,且都满足IBR≥TIBR,如图3a所示。 Figure 2 Error rate of each algorithm under different n图2 不同标签实际数量n下各算法的误差率 Figure 3 Adjusting process of IBR under different n图3 不同规模标签群上IBR的调整过程 对于不同b值下的OBTT算法误差率曲线,其每个波峰的出现即代表此时的IBR趋近于0,需要增加时隙调整S值重新估计标签数量,如b=96,n=950时,此时时隙消耗数量与标签实际数量在正无穷方向的某个区间上一定是单调递增的。 随着标签实际数量的不断增大,OBTT算法的IBR值不断减小直至IBR=0时才增加时隙调整S值,而OBE算法根据TIBR不断调整S,使其IBR值始终维持在TIBR以上,如图3b所示。因此,从仿真结果中能够看出,OBTT算法的估计性能随着标签实际数量的增大而出现下降,而OBE算法的误差率,基本维持在0.12%左右。 标签数量的估计本质上是对1个随机过程进行估计,由于其不可避免地会出现随机性误差,所以要求标签估计算法应该具备一定抵抗随机性误差的能力。在不同规模的标签环境中,其仍具有准确的标签估计性能,这种能力被称为标签估计的稳定性。本节通过分析在不同b值下,OBTT算法和OBE算法在标签数量为50~2 000时估计误差率的标准差来分析2种算法的稳定性。 从图4中可以看出,OBE算法的稳定性明显高于OBTT算法的。随着b值的不断增大,2种算法的估计性能趋稳定,这是因为b值越大,标签可选的比特位置越多,根据二项分布特性,其出现的空闲比特率也将越大,因此估计更加准确。虽然较大的b值可以提高标签估计精度,同时也会带来标签成本增加,标签与读写器之间的通信开销增大等问题。 Figure 4 Stability of OBE and OBTT algorithms under different ID lengths图4 不同ID长度下OBE和OBTT算法的稳定性 本节给出了在不同标签ID长度下,OBTT算法和OBE算法的时隙消耗在标签实际数量为50~ 2 000时的变化曲线图,如图5所示。 Figure 5 Slot consumption of tag number estimation图5 标签估计的时隙消耗 从图5中可以看出,2种算法的时隙消耗数量均与标签实际数量成正比,且OBE算法的时隙消耗量要大于OBTT算法的。这是因为OBE算法需要不断调整S值的大小,使得IBR≥TIBR。每1次S值的调整都需要消耗1个时隙,因此OBE算法相比OBTT算法的时隙消耗较高,即OBE算法的标签估计时间要长于OBTT算法的。 本文在研究OBTT算法的基础上,提出了基于比特估计的OBE算法,该算法针对OBTT算法中使用单个空闲比特位作为开启标签估计准则的缺陷,给出了1种新的开启标签估计的准则,通过引入TIBR参数用于判定当前比特字符串中的空闲比特率情况而决定是否进行标签估计。通过计算机数据模拟,确定了适用于稠密标签环境中的最优TIBR取值。仿真结果显示,与OBTT算法相比,OBE算法的估计性能要优于OBTT算法的,估计误差率维持在0.12%,且标签估计的精度基本不受标签实际数量和标签ID长度的影响。 尽管OBE算法具有较高的标签估计准确性,对标签进行估计时,由于可选的字符串比特位数S远小于标签实际数量n,因此存在IBR远小于TIBR的情况,使得读写器需要多次发布调整L值指令才能准确估计出标签的数量,但这在稠密的标签环境中,将大大增加标签和读写器之间的时隙消耗以及通信开销,造成相对较长的标签估计时间。因此,下一步将优化OBE算法中标签与读写器之间的数据交换机制,降低2者之间的通信开销,使之能够应用于实际的RFID系统当中。
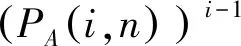
4 仿真实验
4.1 标签估计的误差率
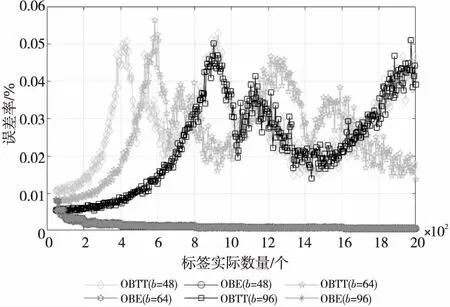
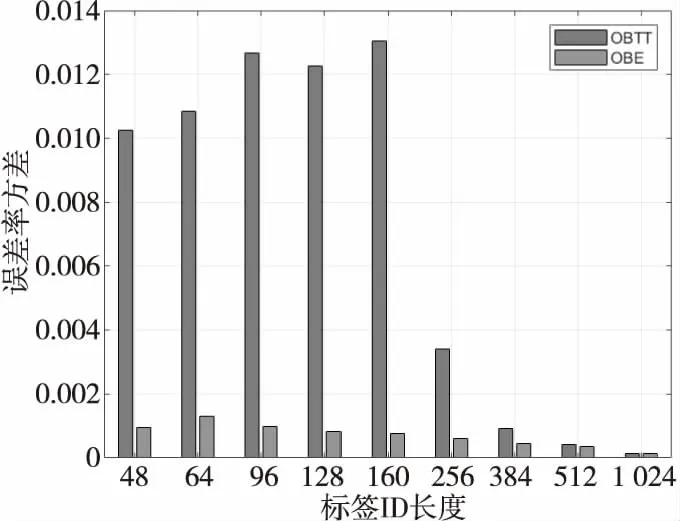
4.2 标签估计算法的稳定性
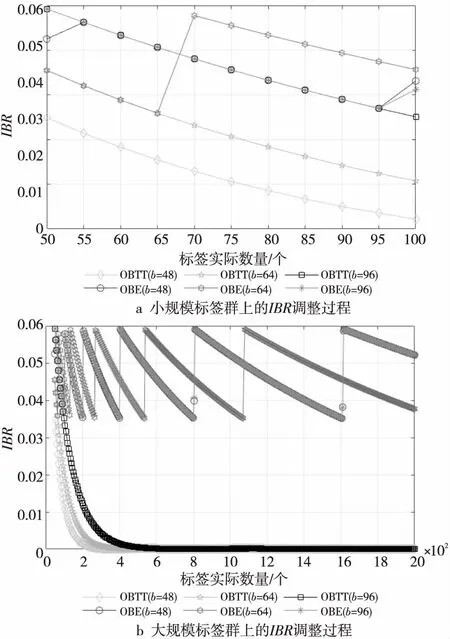
4.3 标签估计的时隙消耗
5 结束语

