基于改进蚁群算法的物流运输路径研究*

马贵平,潘 峰

(西南交通大学希望学院，四川 成都 610400)

1 引言

随着经济和科学技术的发展，网上购物逐渐成为人们必不可少的生活方式，这种购物方式不仅大幅度便利了人们的生活，而且还带动了物流行业的快速发展。物流作为“第三利益源泉”对经济发展的影响日益明显，越来越多的企业也纷纷加入其中，物流逐渐成为当今竞争激烈的行业之一。如何实现科学物流配送是每一家物流企业必须面对的一个非常繁琐而且至关重要的难题，物流企业都需要在运输过程中实现低成本、高效率的目标。在物流配送中，物流运输路径的选择问题尤为关键，它是每一家物流企业都需要解决的难题。在物流运输过程中，降低企业物流成本，缩短运输时间，提升运输服务质量，获得运输最优路径是学者们研究的目标。为此本文提出基于改进蚁群算法的物流运输模型来降低物流运输成本,提高运输效率。

2 车辆路径优化的问题

车辆路径优化问题VRP(Vehicle Routing Problem)是物流配送优化过程中的重要研究对象，车辆路径优化问题被明确定为NP-hard问题，随着配送货物数量不断增加，传统路径规划算法并不能在较短时间内获得最优解，这类组合优化问题利用仿生优化算法能更好地进行求解。国内外学者都提出了大量的算法对该类问题进行求解,例如王迎等[1]提出一种加入混沌扰动的模拟退火蚁群算法CSAACO(Chaotic-Simulated Annealing Ant Colony Algorithm)，该算法设定了寻找的范围，对信息素更新方式加以改进，提高了算法的全局寻优能力，在求解效率和精度方面优于传统蚁群算法；龙汀等[2]提出利用蚁群算法的思想求解VRP问题，该思想利用一种改进的蚁群算法来求解带时间窗的VRP，通过加入伪随机等相关参数来改进传统蚁群算法，最后通过仿真模拟实验测试，实验结果表明该算法能有效获得全局最优解，加快算法收敛速度；赵美红[3]在标准蚁群算法基础之上，对信息素更新方式进行改进，并且加入最近邻域算法以及局部最优搜索策略来解决算法初期的蚂蚁路径选择问题，同时利用动态信息素更新方法对标准蚁群算法进行优化改进，使算法趋于全局收敛，实验表明算法的性能得到了有效提高；王蕾等[4]搭建了多子群蚁群算法，利用各子区间之间的信息排斥与依存关系，加快最优线路的搜索速度，缩短了运行任务所需要的时间。

物流路径优化的问题是一个典型的组合优化问题，是极为复杂的系统性问题，上述研究在一定程度上改善了该难题。本文在以上研究基础之上，提出采用改进蚁群算法来有效改进目前运输车辆在选择路径时存在成本高、效率低下等问题，并与文献[1]中的CSAACO算法和传统的蚁群优化ACO(Ant Colony Optimization)算法进行仿真实验对比，来验证本文改进算法的可行性和有效性。

3 传统蚁群算法

ACO算法是一种人工智能优化算法，用以模拟自然界蚁群在搜寻食物过程中探索线路的行为。蚁群优化算法表明蚂蚁能够根据前面蚂蚁所分泌的信息素来选择路径，其选择食物源线路的通往概率与该线路上分泌的信息素强度成正比。因此，在蚂蚁经过的路径上会形成一种信息的反馈现象，即选择某1条路径的蚂蚁数量越多，该路径上所留下的信息素就越多，后面的蚂蚁选择该条路径的可能性就越大，以此达到寻找到最短路径的目的。

假设有m只蚂蚁，并且蚂蚁全部从规定出发点出发，假设它们到达食物的道路上分布有n个节点，τij(t)表示节点i和节点j之间的路径上在t时刻的信息素浓度，ηij(t)为路径i→j对应的启发信息函数，则对某1只蚂蚁k，从节点i爬行到下1节点j的概率为：

(1)

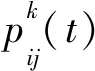
τij(t+1)=(1-ρ)τij(t)+Δτij(t)

(2)

(3)

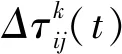
4 改进蚁群算法模型

传统蚁群算法优点较多，如算法鲁棒性较强，采用正反馈算法，并且容易和其他算法相结合等。但是，传统蚁群算法也不可避免地存在一些缺陷，例如，容易陷入局部最优解而导致搜索停止现象，而且搜索时间较长，在解决车辆路径优化这类NP-hard问题时，传统蚁群算法寻求最优解的速度和效率就会变得相对较低。在应用传统蚁群算法优化物流运输路径过程中,常见的方法是求解出物流运输起始点到终点之间的最短距离,此类算法主要考虑的是利用路径长短来衡量解的优劣。但是，在物流运输过程中，有必要考虑所选择道路的平均通畅程度，所产生的运输成本以及运输时间等因素。因此，道路的选择其实是1个多约束条件下的求最优解的问题。为此，本文在标准蚁群算法基础之上，加入基于多个约束条件的最优路径选择的改进蚁群算法，在传统蚁群算法基础之上对启发函数和信息素更新方式分别进行改进，利用下1节点到终点的距离来改进蚁群算法中的启发函数；通过由物流运输时间因子、物流运输成本因子和道路平均通畅程度因子组成的约束函数模型来改进算法中的信息素更新方式。改进后的蚁群算法使得物流运输时间更短，运输途径更短，运输效率更高。

5 改进启发信息模型

在传统蚁群算法公式中，启发函数只考虑相邻2个节点之间的距离的倒数1/dij，但这样的方式只反映了当前节点与相邻节点的关系，没有反映当前节点和目标点的关系。这种局部的搜索范围是以当前节点为中心，周围节点为半径的类似圆形的区间，这种没方向性的搜寻方式容易让蚂蚁陷入局部最优，只能搜索出局部最短路径，而且容易导致得到的解并非全局最优路径，从而失去了全局搜寻最优解的能力。针对该问题，可将下1个节点j与终点g之间的直线距离加入到启发函数中，表达式如下所示：

(4)

其中，dij表示当前节点i到下1个节点j之间的距离，djg表示当前节点j到节点g之间的距离。将下1节点和终点之间的距离引入启发函数，增强了蚂蚁搜寻的目的性，可加快算法收敛速度。若djgdij,则规定节点j为近距离节点。当蚂蚁搜索时，对于远距离的节点无需搜索，只需计算距离i较近的几个节点，利用此改进方法，能够进一步减少计算量，加快算法收敛速度。因此，利用式(5)对传统蚁群算法进行改进：

(5)

5.1 改进信息素更新模型

基于物流运输过程中，最优路径的选择主要考虑几个关键因素：运输的时间、成本、道路平均通畅程度。为了更快获取最优解，本文通过设置运输时间因子、运输成本因子、道路平均通畅程度因子来对路径选择建立基于多个约束因子的数学模型X(j)，并将该模型融入到标准蚁群算法当中,实现基于多约束条件的路径实时更新和动态选择,引导物流运输选择朝最优路径前行,更加精确地得到最优解。

5.1.1 物流运输时间因子

(6)

其中，Tjmax表示物流在道路运输过程中允许的预估最长时间上限，Tj表示物流运输所需的实际时间，并且

Tj≤Tjmax

(7)

X1(j)为物流运输时间因子，表示物流运输到节点j的实际运输时间与预估最长时间的比值。该比值越大，说明实际运输时间越长。

5.1.2 运输成本因子

(8)

其中，X2(j)表示运输成本因子，表示物流运输到节点j的实际运输成本fj与最大预估运输成本fj max的比值，该比值越大，说明实际运输成本越高。

fj=abrasionj+Tollj+Fuelj

(9)

fj≤fjmax

(10)

其中，abrasionj表示道路运输过程中的磨损费；Tollj表示通行费；Fuelj表示燃料费。

5.1.3 道路平均通畅程度

(11)

其中，X3(j)表示物流运输到节点j的过程中，运输到节点j的路径的通畅程度与车辆行驶道路通畅度最低容忍度的比值，该比值越大，说明运输车辆选择该路径行使过程越通畅;Clj表示运输到节点j的路径的通畅程度;Cljmax表示车辆行驶道路通畅度的最低容忍度。

综上，约束函数X(j)表示如下:

X(j)=εX1(j)+φX2(j)+γX3(j)

(12)

其中,X1(j)表示物流运输时间因子，X2(j)表示物流运输成本因子，X3(j)表示道路平均通畅程度因子，ε、φ、γ分别表示在物流运输到节点j的过程中所花时间、成本、道路平均通畅程度所占权重。

5.1.4 最优最差路径优化

为了加快算法的收敛速度，对质量路最差的径进行削弱，加入惩罚因子，降低其被选择的概率，增强质量较好的路径上的信息素浓度，使蚂蚁选择质量更佳的路径。对标准蚁群算法中信息素更新公式改进如下：

(13)

式(13)中引入参数μ，μ∈[0,1]，Dbest表示遍历到的最优路径，|Dbest|表示其长度，Dworst表示遍历到的最差路径，|Dworst|表示其长度,ρ为信息素浓度挥发系数。μ表示改进蚁群算法中的信息素增强因子，对遍历到的最差路径进行惩罚，降低其信息素浓度，对遍历到的最优路径上的信息素进行增强。同时，在改进蚁群算法执行过程中，为了防止路径上信息素浓度无限制地累加，必须对信息素浓度进行限制，约束表达式如下所示：

(14)

其中,τmax，τmin分别表示信息素最大值和最小值。

6 改进后蚁群算法流程

改进后的蚁群算法流程图如图1所示。

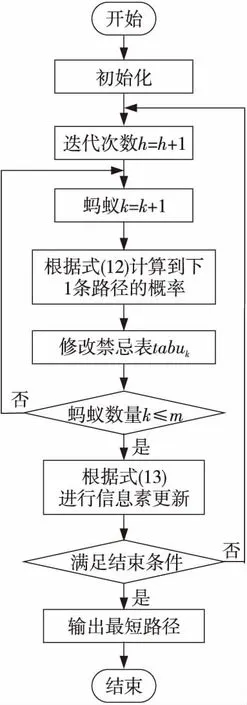
Figure 1 Flow chart of improved ACO algorithm图1 改进ACO算法流程图

7 仿真实验

在仿真实验中,具体的实验环境设置如下:CPU 为2.30 GHz，内存为4 GB，操作系统为Windows 2003，采用 Matlab 7.0实现编程。改进后的蚁群算法参数设定为：蚂蚁数量为100，初始的信息启发因子α=1，期望启发因子β=1，信息素挥发系数ρ=0.5，ε=1/3，φ=1/3，γ=1/3，最大的迭代次数为300次，采用快递物流公司的5个配送网点的数据，其物流配送服务的客户规模如图2和图3的横坐标所示，配送时间缩短量和配送距离缩短量如图2和图3中的纵坐标所示。采用本文改进的蚁群算法、ACO算法和CSAACO算法分别对物流运输车辆进行最优路径求解，求解结果用图2和图3中的折线表示。

从图2可以看出,改进算法的平均寻优路径的时间比ACO算法和CSAACO算法的分别缩短258 004 s和15 000 s；当客户规模在100～200时，传统的ACO算法、CSAACO算法和本文的改进算法的任务时间方面差异不是那么明显，当随着客户规模不断增加，在执行同样规模任务的情况下，本文算法的时间远低于CSAACO和ACO的，本文算法能够弥补CSAACO算法和ACO算法的寻优时间较长的不足，具有更快的求解速度。

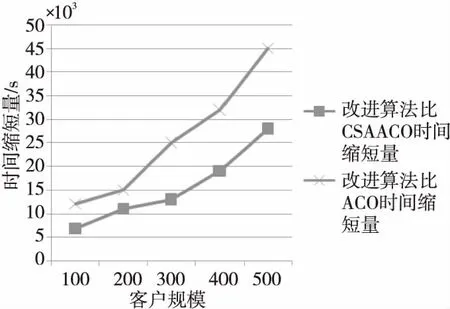
Figure 2 Relationship between customer size and time shortening图2 客户规模与时间缩短量的关系

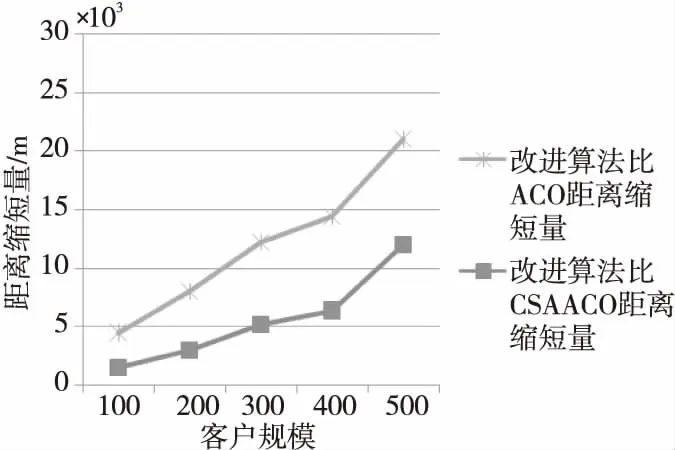
Figure 3 Relationship between customer size and distance reduction图3 客户规模与距离缩短量的关系

从图3可以看出,本文改进算法的求解路径距离相比ACO和CSAACO分别减少25 000 m和5 854 m。当客户任务规模为100时，本文算法与CSAACO算法相比，距离缩短了约2 650 m；改进算法与传统ACO算法相比，距离缩短了约5 000 m；而且随着规模的增加，差距在逐渐扩大，本文改进算法表现出来的优势更加明显，具有更好的路径寻优能力。

以上实验结果表明，改进算法在寻优效率和寻优质量方面相比于CSAACO算法和ACO算法都有着明显的提升。特别是随着服务客户的规模不断扩大，该算法能更有效地解决物流配送耗时长和求解质量差等问题，优势得到了更好的体现，利用本文改进蚁群算法在同样客户规模任务的情况下，能够有效缩短执行配送任务的时间，减少运输路径距离，加快算法收敛速度，最大化地提高物流行业整体配送效率。

8 结束语

物流运输的路径选择问题对物流企业的运送成本、时间与效率的影响至关重要，是所有物流行业所面临的难题。本文在传统蚁群算法基础之上对路径上的信息素浓度进行限制，同时加入基于运输时间、成本、道路平均通畅程度因子的约束条件，改进信息素更新方式，从而改变了物流路径转移概率，增加了全局寻优能力，缩短了配送路径，降低了物流企业配送所花费的成本，提高了配送效率，促进了物流行业的快速发展。