一种基于周期性特征的数据中心在线负载资源预测方法*
梁 毅,曾绍康,梁岩德,丁 毅
(北京工业大学信息学部,北京 100124)
1 引言
随着大数据产业的发展,数据中心得到了较为广泛的关注和较大的投入建设。负载是数据中心应用的运行实例,也是数据中心资源使用的主体。以Web服务、流式计算为代表的在线负载是其中一类长时运行、延迟敏感的负载。由于在线负载受到用户行为驱动,负载强度具有较大的波动性,在运行过程中其资源需求动态变化。在线负载资源需求预测一直以来都是数据中心资源管理领域的研究热点。快速、准确的在线负载资源需求预测是数据中心合理分配资源、保障负载执行效率的关键。
数据中心在线负载资源预测方法已得到广泛关注和研究。总结而言,既有方法可分为3类:基于简单统计分析方法、基于时间序列分析方法和基于机器学习方法。
简单统计分析方法是指通过对资源使用数据采用统计分组、相关分析等方法分析在线负载资源使用情况,对当前在线负载资源需求进行预测[1,2]。然而,单纯采用简单统计分析的方式无法更准确地挖掘在线负载资源使用的特征和变化趋势。
针对简单统计分析方法的不足,时间序列分析方法被引入数据中心资源预测。既有工作主要采用AR(Auto Regressive model)分析法[3 - 5]、自相关和互相关方法[6,7]以及ARIMA(Auto Regressive Integrated Moving Average)方法[8 - 13]对数据中心单负载及混部负载场景下应用的CPU、内存、磁盘及网络资源需求进行预测。然而,上述时间序列分析方法多适用于短期预测,难以对在线负载的长时运行的资源需求进行准确预测。
随着机器学习的发展,相关算法被广泛应用到了在线负载资源预测中。既有工作主要采用多元线性回归方法[14 - 16]、聚类方法[17,18]、支持向量回归方法[19 - 21]及马尔科夫模型[22 - 25]进行应用资源使用预测。文献[26]针对在线负载,测试了线性回归、神经网络和支持向量回归等算法在CPU需求预测上的性能,发现在各算法中支持向量回归算法的预测结果更准确且表现最优。然而,机器学习算法的预测准确度依赖于大规模样本数据的训练,而大规模数据的训练会导致较大的时间开销,无法满足在线负载实时性的场景。
然而,上述研究成果尚存在2点不足:(1)既有基于简单统计分析和时间序列分析的预测方法多着眼于短期预测,难以获得较为准确的长期预测值;(2)既有基于机器学习的预测方法准确度依赖于大规模样本数据,且具有较大的时间开销,难以适应在线负载快速响应、延迟敏感的需求。
针对上述问题,本文将在线负载资源使用的周期性特征引入资源预测中,提出基于周期性特征的在线负载资源预测方法PRP(Periodical characteristic based Resource Prediction)。PRP通过资源使用变化周期识别和资源使用样本子序列分类,将在线负载的长期资源预测转化为短期预测,通过加权综合不同类资源使用子序列获得快速、准确的在线负载资源预测。本文的主要贡献可归纳为3个部分:
(1)提出了基于自相关函数的在线负载资源使用周期识别方法。应用自相关函数对在线负载资源序列的周期进行识别和量化,利用其周期性特征将长期资源预测转化为周期间资源使用的比对统计。
(2)提出基于K-Means聚类的资源使用子序列分类方法。针对资源使用量以及变化趋势,采用K-Means聚类算法对按照周期划分的子序列集进行分类;最终依据分类,采用线性加权方法计算资源需求预测值。
(3)对本文提出的在线负载资源预测方法PRP进行了性能评测。实验结果表明,与既有基于ARIMA算法、支持向量回归算法和马尔可夫模型的在线负载资源预测方法相比,PRP方法可使预测平均相对误差最大降低28.3%,12.3%和27.4%。同时,随着预测时间步长的增加,PRP方法在预测准确度和时间开销上的优势逐步增加。
2 在线负载周期性特征分析
本节将分析在线负载资源使用的周期性特征。
2.1 任务知识
请求到达波动性是在线负载的典型特征。随着在线负载用户群体的扩增、服务访问或数据采集行为习惯的趋同,负载请求波动的周期性特征具有一定的普遍性。图1中展示了3个不同的在线负载场景下请求强度的变化统计。
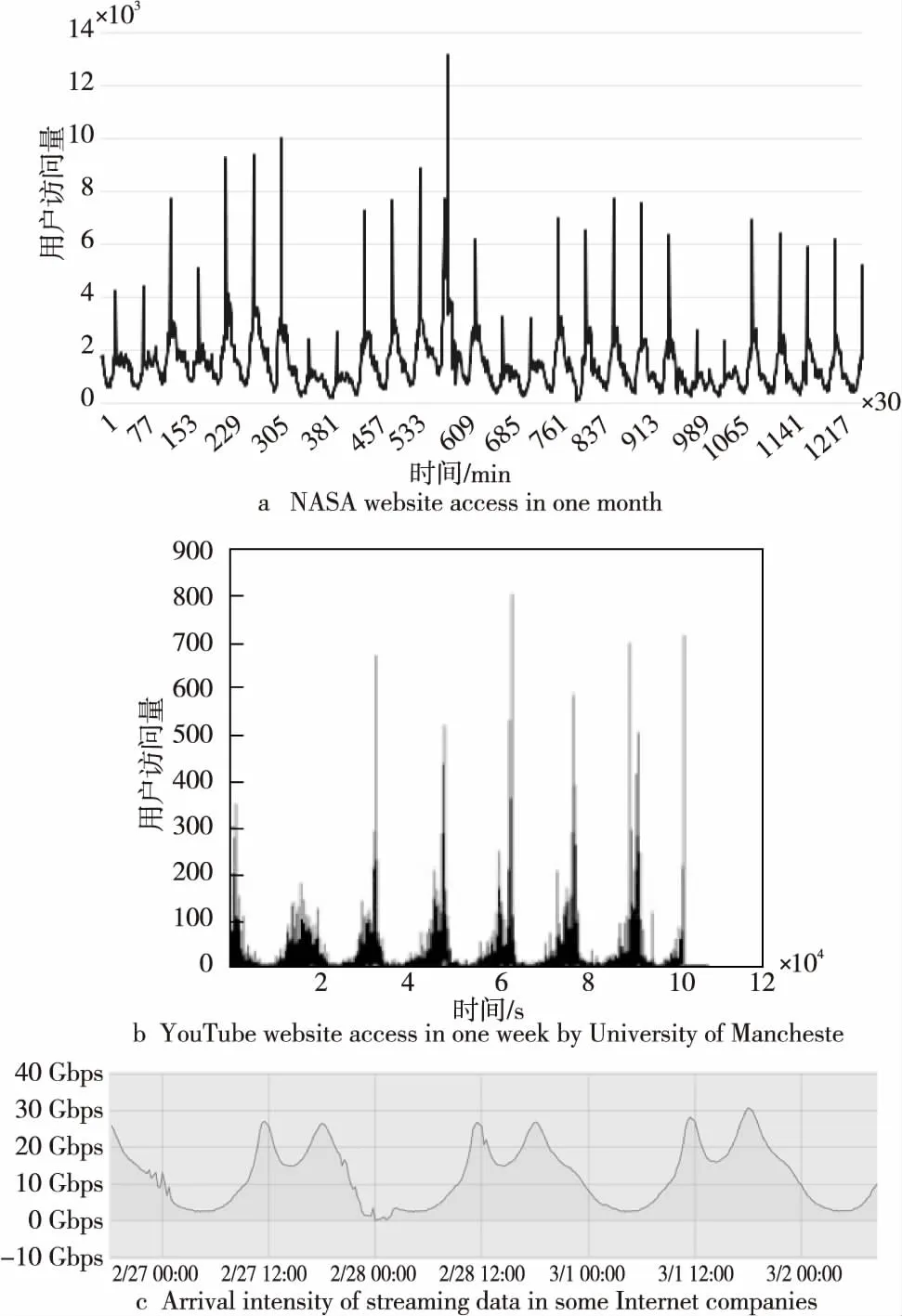
Figure 1 Examples of online workload user request/data arrival intensity图1 在线负载用户访问量/数据到达强度
从图1中可以分析出,在线负载请求强度呈明显的周期性变化,在周期内数据呈相似的变化趋势。以图1a NASA网站1个月的用户访问量为例,其用户访问以24 h为1个周期发生变化,大多数周期内的用户访问量在500~8 000次以相似的趋势波动。但是,也有少数周期内数据量变化有异常现象。其中,在第8和第9个周期内,用户访问量在0~4 000 波动,在第13个周期内,用户访问量最多达到了13 000以上。同样,图1b和图1c分别展示了曼彻斯特大学的学生1周内对YouTube网站的用户访问情况和国内某互联网公司的流式日志数据到达强度趋势,其中流式日志业务是在线负载中典型的流式计算负载。除此之外,伯克利大学主页访问、法国世界杯体育网站[27]访问等数据也均呈现为较典型的周期性特征。具体而言,上述在线负载的访问具有如下共性特征:(1)负载请求以小时、天或者周为周期,具有相同的变化趋势;(2)大多数周期间,数据的变化幅度相同或相似,存在少量周期间数据变化幅度有较大差异。
2.2 在线负载资源使用周期性特征分析
在线负载请求到达强度是影响其资源使用的核心因素,本文提出假设:周期性的用户访问/数据到达强度会引发在线负载的周期性资源使用特征。为此,通过1组实验进行分析。
既有数据中心多采用容器技术部署在线负载,并进行资源隔离。因此,本文假设数据中心多在线负载间的资源使用干扰较小。基于容器技术,部署单在线负载,分析其资源使用特征。本文采用典型的Web类型负载——TPC-W,在数据中心单在线负载的场景下,设置用户访问量变化周期为1 h,周期内用户访问符合正弦分布,用户访问强度为40次/秒~120次/秒。
以上实验展示了在周期性的用户访问强度下,在线负载资源使用变化的情况。分析可知,在用户访问强度变化以1 h为周期的情况下,其资源使用量的变化周期也为1 h。另外,在相同的用户访问强度下,每个资源周期内的数值波动范围相同,周期间的变化趋势也有较强的相似性。在第3个周期(图2中横坐标170~230),我们将请求强度变化从40次/秒~120次/秒提高到40次/秒~160次/秒,在图2a中可以看到,在本周期内负载的内存使用量变化从1 700 MB~2 500 MB变为1 700 MB~2 700 MB,增长明显。同样,在第7个周期(图2中横坐标410~470),将线程变化从40次/秒~120次/秒降低到40次/秒~80次/秒,其内存和CPU使用量在第7个周期内也呈现明显的降低。

Figure 2 Variations in resource consuming of online services图2 在线负载运行的资源使用情况
综上,具有周期性请求/数据到达强度的在线负载,其资源使用量会随着请求/数据到达变化,且呈现相近的周期特征。
3 基于周期性特征的在线负载资源预测方法PRP
本文将在线负载资源使用的周期性特征引入资源预测中。如图3所示是在线负载资源预测方法PRP的框架。
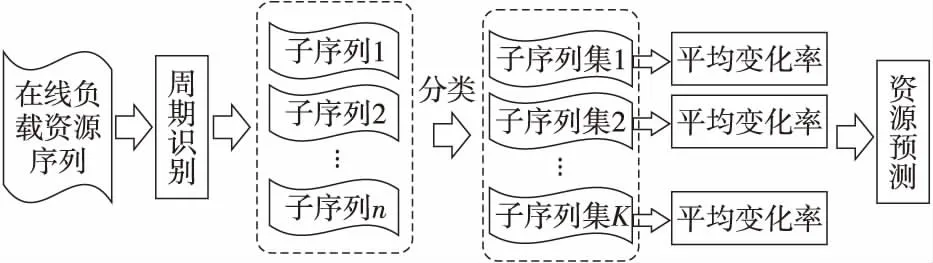
Figure 3 Overview of PRP图3 在线负载资源预测方法PRP框架
PRP方法首先应用自相关函数法对在线负载资源使用量样本序列进行周期识别;其次将样本序列依据周期进行划分得到子序列集;再次计算所有子序列间的相似度,并根据相似度进行子序列划分;最终根据预测时刻点在各类子序列中对应时刻点的资源使用变化率计算资源需求预测值。
3.1 在线负载资源使用的周期识别
本文选用自相关函数方法对在线负载的内存和CPU资源使用量进行周期量化识别。自相关函数被广泛用于信号的潜在周期性检测中。对于1个有限长度的离散序列,当序列中2个变量存在关系时,随着其中1个变量数值的确定,另1个变量会有不同的取值,但是该变量的取值有一定的规律性。这种统计规律可以通过自相关函数来表示,如式(1)所示:
(1)
其中,N是有限长的离散序列y的长度,x表示元素下标,k表示自变量。
自相关函数有以下性质:
性质1周期函数的自相关函数依然存在周期性,并且其周期性与原函数周期频率相同。
性质2自相关函数具有偶函数特点,即R(k)=R(-k)。
性质3任意函数的自相关函数都会周期性地存在极大值和极小值,并且在相邻的极大值和极小值之间,自相关函数是单调的。
本文的目的是利用自相关函数的特性计算出内存和CPU使用量序列的周期值。
由于内存和CPU的预测方法以及周期相同,因此,下面均以资源使用序列统一指代内存和CPU序列,L={l1,l2,…,ln},其中li表示第i个时间点对应的资源使用量,n为资源使用量样本总数。具体的判别和度量流程如下所示:
方法1在线负载资源使用周期识别方法
(1)收集在线负载资源使用数据;
(2)以5 s为固定步长,截取样本数据,构建在线负载资源序列ML;
(3)根据式(1)计算出序列ML的自相关序列MR;
(4)求取MR中任意2个相邻的极大值,计算它们的时间距离t_maxi;
(5)将所有t_maxi求和,然后取平均值;
(6)所得到的平均值即为资源使用序列ML的周期。
3.2 在线负载资源使用样本子序列分类
在线负载资源使用样本子序列分类的目的是在序列周期识别的基础上,统计具有不同资源使用量及变化趋势的子序列类,最终为资源预测提供依据。
本文采用欧氏距离作为资源使用样本子序列间相似度度量,称为子序列距离,计算如式(2)所示:
(2)
其中,pi表示第i个序列,pj表示第j个序列,pik表示第i个序列中的第k个元素数据,同理,pjk表示第j个序列中的第k个元素数据。
显然,子序列距离越大,序列间相似度越小,反之则序列间相似度越大。同时,本文采用聚类方法对资源使用样本子序列进行分类。如第2节所述,在线负载资源使用的周期性特征呈现出多数周期间资源使用量值及变化幅度相同或相似,少数周期间则存在较大差异的特点。因此,本文将在线负载资源使用样本子序列分为常规序列和异常序列。其中,常规序列是指在线负载资源使用子序列中数据变化范围相似的大多数的子序列,异常序列是指在线负载资源使用子序列中数据变化发生异常的子序列。本文首先给出如下定义:
定义1全局子序列最大距离:所有资源使用样本子序列之间距离的最大值dmax:
dmax=max({d(xi,xj)|xi∈X,xj∈X})
(3)
其中,d(xi,xj)表示xi、xj之间的距离,X表示样本序列集合。
定义2全局子序列最小距离:所有资源使用样本子序列之间距离的最小值dmin:
dmin=min({d(xi,xj)|xi∈X,xj∈X})
(4)
其中,d(xi,xj)表示样本序列xi,xj之间的距离,X表示样本序列集合。
定义3子序列类距离阈值:所有资源使用样本子序列类中序列之间距离的最大值:
α=(dmax-dmin)×a+dmin
(5)
其中,0 本文选择K-Means聚类算法[24]进行在线负载资源使用样本子序列分类,它将1个给定的数据集划分为用户指定的k个聚簇,有着较高的执行效率。在线负载资源使用子序列分类的K-Means算法如算法1所示。 算法1在线负载资源使用子序列分类的K-Means算法 输入:在线负载资源使用子序列集,子序列类距离阈值α,常规子序列占比阈值δ,子序列分类数K。 输出:子序列分类集合C。 1C←∅;/*初始化子序列分类集合*/ 2O←∅;/*初始化中心点集合*/ 3 Fori 4oi←RandomSelect(X); 5O←O∪{oi}; 6 End For 7 Repeat: 8 ForxiinXDo: 9j←MinDistance(xi,O); 10Cj←Cj∪{xi}; 11 End For 12 Fori 13max_point_distancei←MaxDistance(Ci);/*计算每个簇内最大距离*/ 14maxD←maxD∪{max_point_distancei}; 15si←Scale(ni,N);/*计算每个簇内数据量占总的子序列数量比例*/ 16maxS←maxS∪{si}; 17 End For 18maxDistance←Max(maxD);/*计算所有簇距离的最大值*/ 19maxScale←Max(maxS);/*计算所有簇所占子序列总量比值的最大值*/ 20 UntilmaxDistance<α&maxScale>δ; 21 ReturnC 算法1依据用户指定的子序列分类数量进行子序列聚类,从所有在线负载资源使用样本子序列中随机选取初始类簇中心点,并进行迭代计算。其迭代收敛条件有2个:(1)任一类簇中子序列的最大距离不超过定义的阈值,这保障了所获得的子序列分类中,每一类子序列间具有相似的资源使用量和变化规律;(2)规模占比最大的类簇其规模占比应超过设定的比例阈值,这是因为根据本文第2节的观测结果,在线负载资源使用周期性呈现出多数周期间资源使用量及变化规律相似,少数周期间差异较大的特点。通过约束规模占优子序列类的占比阈值,进一步保障聚类结果与实际场景中子序列分类情况吻合。 在周期识别和序列分类的基础上,本节提出具有周期性特征的在线负载资源预测方法。 令NL={nl1,nl2,…,nlS}表示资源使用样本集合,其中nli(1≤i≤S),表示第i类子序列集合,S是样本类总量,nli={sli_1,sli_2,…,sli_K}表示按时间排列的第i类样本子序列集合,K是序列类的总量。sli_j={eli_j_1,eli_j_2,…,eli_j_T},1≤j≤K,eli_j_t表示1个采样周期内第t个采样时刻的资源使用量,1≤t≤T,T是采样周期时长。本文首先给出以下定义: 定义4子序列类比例:在经过周期分割的所有在线负载资源使用子序列中,每一类子序列所占子序列总数的比例,可以用式(6)表示: (6) 其中,|nli|为第i类子序列集合中的序列总数,S是样本类的总量。 定义5子序列资源使用变化率:对任意子序列中采样时刻t的资源使用变化率Rnli_j_t可表示为: (7) (8) 定义7子序列资源预测值:第i类子序列在下1个周期的采样时刻t的资源使用预测值pli_t可表示为: pli_t=eli_K_t×(1+Anli_t) (9) 定义8在线负载资源预测值:最终的在线负载在下1周期t时刻的资源使用预测值lnext_t可表示为: (10) 其中,wi为第i类样本子序列的预测权重。 由上述定义可知,对于在线负载资源需求的预测实质上是依据历史资源使用样本数据中各类样本子序列出现的概率,对子序列中对应时间点的资源使用变化率进行加权平均,进而形成预测时间点相对于上1个周期相应时间点的资源使用变化率,最终计算出预测时间点的资源需求量。 本节从预测准确度和计算效率的角度对PRP方法进行性能评测。针对在线负载的主要资源需求,选取CPU和内存2类资源进行预测。 本文分别选取TPC-W和HiBench中的流式计算负载WordCount作为测试负载。上述负载分别是在线负载中Web服务和流式计算的典型代表。负载的请求/数据到达强度符合泊松分布和正弦分布。测试基础环境由5台服务器组成,服务器具体配置包括:Intel(R) Xeon(R) CPU E526600@2.20 GHZ*4,16 GB内存,1 TB磁盘,千兆以太网。实验软件环境主要包括Apache 2.4和Spark 2.3.1。实验选取预测平均相对误差(MRE)作为预测准确度的量化评价指标;选取预测时间开销作为预测计算效率的量化评价指标。 Figure 4 MRE of memory utilization prediction of streaming workloads图4 流负载内存资源预测误差 实验选取既有成果中基于ARIMA算法、马尔可夫(Markov)模型以及支持向量回归(SVR)的在线负载资源预测方法进行性能对比。这3种方法分别作为时间序列分析类和机器学习类方法被广泛应用于在线负载资源预测问题,是较为有代表性的预测方法。 为了模拟长期预测,本文根据样本中包含的采样时刻点数量M,从第2M的时刻点开始对每隔30 s的资源需求进行预测,预测总量为100个时间点。 实验选取WordCount作为流式计算负载,设置请求/数据到达服从泊松分布,通过配置不同的请求/数据到达强度以及变化周期构造不同的资源使用周期性特征,具体配置如表1所示。预测的样本数据通过运行一段时间负载获得,采样周期为5 s,样本规模分别为10 800,14 400,18 000。 图4和图5分别展示了在数据到达符合泊松分布的情况下,PRP方法和其他对比方法的预测平均相对误差。由图4和图5可知,在各种数据到达强度-周期配置下,PRP的预测准确度均优于既有方法的,其中,CPU和内存资源预测平均相对误差最大分别下降了25.4%和27.9%。同时,实验显示随着样本规模的减小,PRP的预测准确度优势更为显著。这是因为,PRP方法利用周期识别,将长期资源预测转化为短周期内资源的比对预测,克服了既有方法对于大规模样本数据的依赖。因此,PRP方法在样本数据有限或长期预测的场景下具有较好的性能优势。 Figure 5 MRE of CPU utilization prediction of streaming workloads图5 流负载CPU资源预测误差 Table 1 Data arrival and variation period settings 取值组数据到达强度/(MB/s)周期/min1[1,5]152[1,10]153[1,20]154[1,5]305[1,10]306[1,20]307[1,5]458[1,10]459[1,20]45 实验选取TPC-W作为Web负载,请求到达同样服从泊松分布。对于TPC-W负载通过改变请求发生数量来改变请求的到达强度。请求到达强度与周期设置如表2所示。预测样本数据的获取和规模同4.1节,预测样本获取、样本数据规模以及预测时刻点的选取同4.1节。 Table 2 Request arrival intensity and variation period settings表2 请求到达强度变化和周期变化分组 图6和图7分别展示了在请求到达符合泊松分布的情况下,PRP方法和其他对比方法的预测平均相对误差。由图6和图7可以获得与4.1节相同的结论。对于Web负载,PRP可分别最大降低CPU和内存资源预测平均相对误差22.6%和24.1%。 Figure 6 MRE of memory utilization prediction of web workloads图6 Web负载内存资源预测误差 Figure 7 MRE of CPU utilization prediction of web workloads图7 Web负载CPU资源预测误差 随着样本规模减小,PRP方法的预测性能优势更为显著。然而,相对于流式计算负载而言,Web负载的资源预测平均相对误差平均上升了7.9%。这是由于TPC-W具有更为复杂的计算逻辑,对计算资源消耗的波动较流式WordCount负载更大,在资源使用样本子序列分类数量受限的情况下,仅用较为简单的线性加权方法计算资源预测值,无法更为精细地识别周期内资源使用的变化规律。 本节评测PRP和其他对比方法在不同的样本规模下资源预测的计算效率。实验选取流式WordCount和TPC-W作为测试负载,改变样本规模统计预测所需的时间开销。 对于流式WordCount,实验设置数据到达强度为1 MB/s~10 MB/s,变化周期为20 min,数据到达符合泊松分布。实验结果如图8所示。 Figure 8 Time overhead of resource prediction of streaming workloads图8 流式计算负载资源预测时间开销 以请求到达强度变化为40次/秒~80次/秒、变动周期为20 min的TPC-W负载产生的资源序列为样本数据的情况下,实验结果如图9所示。 Figure 9 Time overhead of resource prediction of web workloads图9 Web负载资源预测时间开销 在上述实验中,PRP的预测平均相对误差均小于其他比较方法的,最小下降率为9.3%(由于篇幅限制,本节不再列出预测准确度的测试数据)。然而,由图8和图9可知,随着样本数据规模的增大,PRP方法在预测过程中的时间开销增长率平均为6.7%,而3种对比方法的时间开销平均增长率分别为16.7%,19.6%和12.5%。这是因为PRP在第1次预测的过程中,已完成周期的识别,结合周期性特征,后面新增加的样本数据不用再进行周期识别,减小了时间开销。而在其他3种方法中,每1次建模和预测都要对全部的数据进行训练,这样才能保持一定的准确度。因此,随着样本的增大,其他3种方法的时间开销明显增加。 综上而言,由于PRP充分利用了在线负载资源使用的周期性特征,将长期预测转化为短周期的资源使用比对预测,因此避免了性能预测中的反复建模问题,在资源使用变化周期被识别后,仅通过简单的周期间资源使用统计即可获得预测值,同时保障了预测的准确性。 针对当前在线负载资源预测方法无法进行长期准确的预测和由于依赖海量样本数据导致的较大的时间开销问题,本文提出了一种基于周期性特征的在线负载资源预测方法PRP。该方法在分析提取在线负载资源使用周期性特征的基础上,采用自相关函数方法量化计算在线负载资源使用周期,根据周期计算结果将资源使用样本序列划分成多个子序列;然后将子序列分类;最后加权综合每一类子序列资源使用变化率,计算在线负载资源使用的预测值。大量的实验表明,PRP方法在长期预测的准确度和时间开销方面优于对比方法。 在进一步的研究工作中,将致力于提升样本子序列分类精度,并在此基础上使用更为复杂的资源预测方法进行预测。3.3 在线负载资源预测
4 性能测试与分析
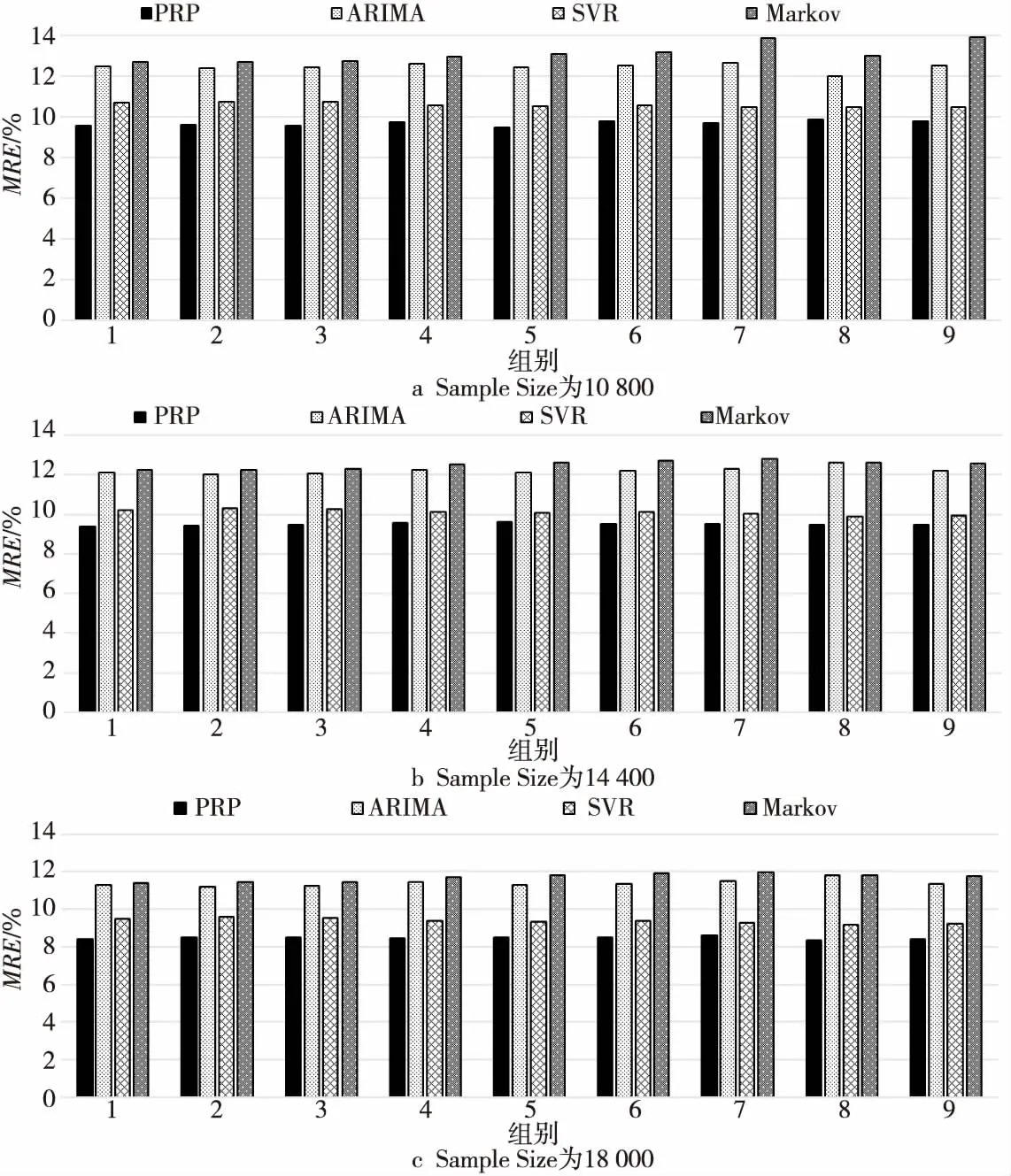
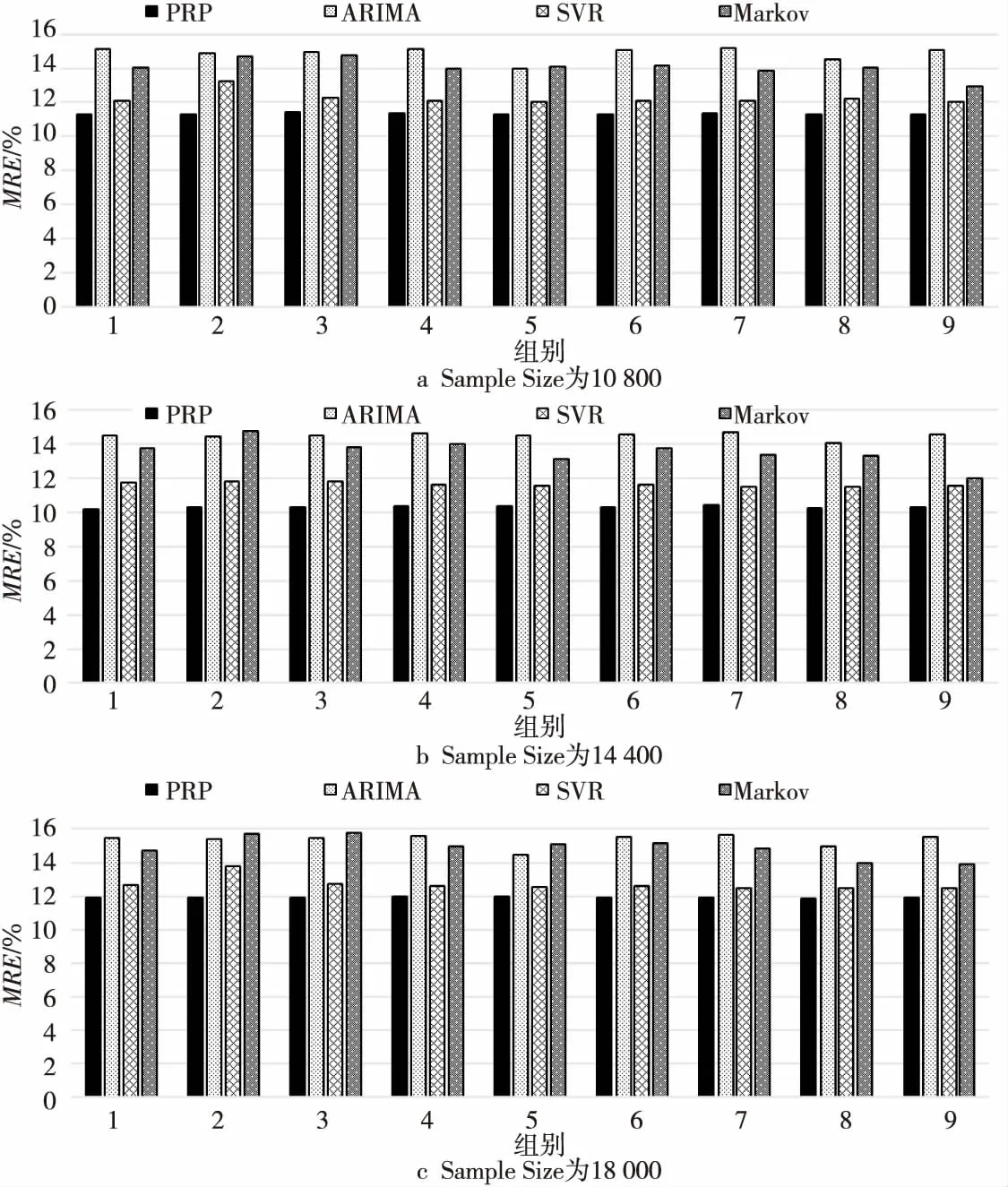
4.1 流式计算负载资源预测准确度评测

表1 数据到达强度和周期变化分组
4.2 Web负载资源预测准确度评测


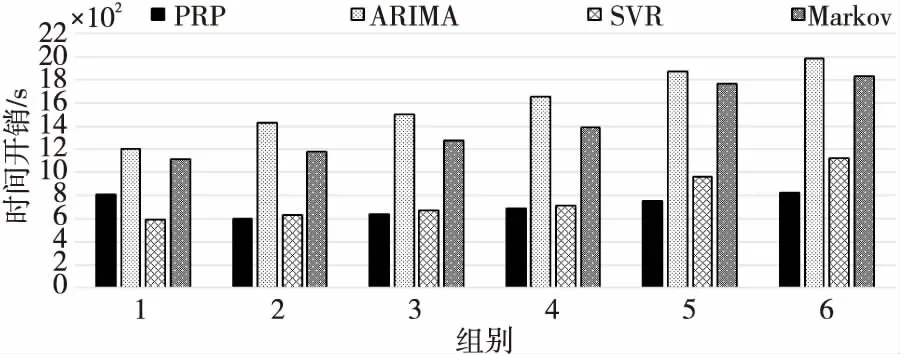
4.3 在线负载资源预测计算效率分析

5 结束语

