WKBZ简正波模型混合并行计算方法研究*
范培勤,刘晓妍,过武宏,崔宝龙
(1.海军潜艇学院,山东 青岛 266199;2.92020部队,山东 青岛 266000; 3.青岛海洋科学与技术试点国家实验室,山东 青岛 266000 )
1 引言
声波是目前唯一能够在海水介质中进行远距离传播的有效载体,掌握和了解水下声传播规律,并做出快速准确的预报,对水声传感器、武器系统的使用和研究都具有极其重要的意义,也是海洋战场环境仿真和“透明海洋”领域的基础研究内容。随着水声传感器、武器装备信息化程度的不断提高,其性能的发挥对环境的敏感性和依赖性更加强烈,如何实时提供精细化、精确化、实时化海洋水声环境信息保障,成为迫切需要解决的难题。随着多核技术的发展,SMP(Symmetrical MultiProcessor)集群在高性能计算领域中所占的份额越来越大,如何充分发挥SMP集群强大的计算能力,提高计算资源有效使用效率,成为HPC领域研究的热点和难点。本文结合SMP集群系统体系架构特点,采用MPI(Message Passing Interface)+OpenMP(Open Multi-Processing)混合编程方法,通过节点内内存共享,节点间消息传递的方式,将并行编程环境与SMP集群的硬件特点进行有机融合,实现了WKBZ模型[1]的2级混合并行计算。测试结果表明,该方法可大幅提高程序的并行效率,同时具有良好的可扩展性。
2 MPI+OpenMP混合并行编程模型
MPI是由工业、科研和政府部门等联合建立的消息传递并行编程标准[2]。它采用分而治之的思想,将大任务划分为若干个小任务分配给集群系统的所有节点,节点间通过消息传递协同工作,最终实现问题的快速处理,具有标准化、可移植、可扩展等特点,适用于几乎所有的高性能计算机系统,是目前SMP集群上主流的并行编程模型。
OpenMP是一种共享内存并行编程模型[3 - 5],通过显式地添加并行编译制导语句来实现程序的并行处理,具有编程简单、移植性好和支持增量并发等特点,是共享存储系统中的并行编程标准。
MPI+OpenMP混合并行编程模型通过在节点内使用共享存储模型、节点外采用消息传递模型实现具体问题的多级并行求解[6]。该模型将SMP集群的硬件特点与并行编程模型有机融合到一起,通过充分发挥2种模型各自的优点,实现SMP集群计算性能的充分发挥,从而获得更高的计算性能和可扩展性。具体来讲:节点间采用消息传递,解决了节点间OpenMP模型计算结果无法交互的问题;节点内采用共享存储,减少进程的数量,缩短了进程初始化和通信所花费的时间。其基本架构如图1所示。

Figure 1 Structure of MPI+OpenMP hybrid parallel programming model图1 MPI+OpenMP混合并行编程模型结构图
3 WKBZ简正波模型混合编程算法的设计与实现
WKBZ简正波模型可准确计算深海环境水下声场的分布,是认识和利用深海中水声传播规律的有效手段,广泛应用于深海环境下水声环境的分析和保障。文献[7]基于PC集群,采用MPI并行编程模型,通过“交叉划分+聚合通信”的方法,实现了1维WKBZ简正波模型的并行计算,可在10-1s的时间内完成1维水声传播损失的计算。为进一步提高水声环境信息保障的精细化程度,利用该方法对2维水声传播并行计算时间进行了测试,结果表明,计算时间随进程数的增加呈现先减小后增加的趋势,计算时间达到了秒级,难以满足为水声环境信息保障提供实时化水声传播数据支撑。通过对测试结果的进一步分析发现,造成这种现象的主要原因是随着进程数量的增加,进程间通信所花费的时间不断增加,并逐渐主导着整个计算时间,严重影响程序的可扩展性。为提高程序的可扩展性,提高计算资源的使用效率,满足水下声场环境仿真对水下声场实时化保障的需求,本文基于MPI+OpenMP混合并行编程的方法,通过节点内共享内存、节点间消息传递的方法,实现了水声环境信息的快速计算,该方法大幅减少了进程间通信次数和数据交互量,有效缩短了通信时间,为实现业务化的水声环境信息保障打下了坚实的基础。
3.1 基于WKBZ的2维水下声场计算
当接收深度、目标深度确定后,WKBZ简正波模型的计算主要围绕着本征值、本征函数、水平距离上传播损失的计算开展,计算量随着频率的增加而增加。为了得到水下2维声场的精细化分布,即考虑目标深度不变,接收传感器在整个水深上变化时所接收到的目标声场分布,将接收深度按照固定的水深间隔向海底方向循环计算,从而得到不同水平传播距离在垂直方向上的声场分布,其计算流程如图2所示。

Figure 2 Flow chart of 2D WKBZ normal model serial computing图2 WKBZ 2维声场串行计算流程图
3.2 基于MPI的并行程序设计与实现
WKBZ 1维声场的并行计算主要采用“交叉划分+聚合通信”的方式围绕着本征值、本征函数和传播损失3部分循环计算过程的并行处理展开,文献[7]已有详细的描述,在此不再赘述。
从图3可以看出,与1维声场计算相比,2维声场的计算主要增加了接收深度循环,即围绕着不同接收深度上本征函数和本征值的循环求解展开,其并行处理可以采用2种方式:
(1)直接在1维声场传播并行计算程序中添加1层深度循环,仍然使用多进程分别完成某1个接收深度上的本征函数、传播损失并行计算,计算完成后再开始计算下1深度的本征函数值和传播损失值。这种方法的实现相对简单,但每个接收深度的计算结束时需要做2次聚合通信和1次广播通信,总的通信次数为接收深度上循环次数的3倍。
(2)对接收深度循环进行并行划分,让每1个进程独立地完成某1个接收深度上的本征函数、传播损失计算,所有进程计算完成后,再通过聚合通信将传播损失值收集到一起。这种方式只需要在每个进程计算完成后进行1次聚合通信,大大减少了通信次数。本文采用此方法来实现基于MPI的WKBZ 2维声场并行计算,计算流程如图3所示。

Figure 3 Flow chart of parallel computing of 2D WKBZ normal model based on MPI图3 基于MPI的WKBZ 2维声场并行计算流程图
基于MPI的WKBZ 2维声场并行计算主要围绕着不同接收深度上本征函数和传播损失的并行处理开展,接收深度的循环次数通常不会超过103次,因此在一定程度上制约着程序的可扩展性。另外,在单个接收深度计算过程中不需要与其他进程进行数据交换,并行计算部分花费的时间通常随进程数的增加线性减少,而每个进程的通信次数和数据传输量相对固定,这将会导致随着计算规模的增加,并行计算花费的时间在整个程序计算时间中所占的比例不断减少,进程间通信时间所占的比例将会不断增加,当计算规模达到一定程度时,通信时间可能会占据主导地位。
3.3 基于MPI+OpenMP的并行程序设计与实现
通过前面的分析可知,2维WKBZ简正波模型的计算过程主要围绕着不同接收深度上本征函数、水平距离上传播损失的计算开展,计算过程可归结为2重循环:第1重为深度循环,即求解不同接收深度上的传播损失值,称之为外循环;另1重为求解具体接收深度上本征函数及不同距离上的传播损失,称之为内循环。2维水声传播模型的求解过程可通过MPI+OpenMP混合2级编程模型与SMP集群的存储结构的特点有机地结合起来。具体来讲:外循环实际上主要完成不同接收深度上水声传播计算任务的分配,是1种粗粒度的任务划分,可通过MPI消息传递的方式实现其并行任务划分;内循环主要完成某个深度上具体的计算任务的处理,内部不同部分间需要进行大量的数据交互,是1种细粒度的任务划分,可采用OpenMP以共享内存的方式实现任务的并行划分。WKBZ简正波模型混合并行算法的计算流程如图4所示。

Figure 4 Flow chart of WKBZ normal model hybrid parallel computing图4 WKBZ简正波模型混合并行算法计算流程图
算法的具体实现过程分为以下几步:
(1)初始化。
完成节点内部的线程数设定和环境参数的读取等初始化工作,再通过MPI_Bcast()函数广播给其他进程。
(2)本征值计算(MPI)。
采用交叉划分方法,将不同号数本征值的求解分配给不同的进程,具体实现见文献[7]。
(3)接收深度循环的划分(MPI)。
采用均匀划分方法,将在深度方向的循环次数分配给不同的进程(第1级循环并行处理)。计算过程伪代码如下所示:
n=waterdeep/NP;
for(i=myid*n;i<(myid+1)n,i=++)
{
#pragma omp parallelprivate(tid)
{
传播损失计算;
}
}
(4)计算划分(OpenMP)。
调用OpenMP的并行编译制导语句,分别实现对本征函数、传播损失并行计算域的创建(第2级循环并行处理)。计算过程伪代码如下所示:
#pragma omp parallelprivate(tid)
{
1例万古霉素致急性肾损伤老年患者行血浆置换术的用药分析和药学监护 ……………………………… 李 薇等(19):2704
tid=omp_get_thread_num();
#pragma omp for//本征函数求解
for(i=0;i { la[i]=la(vl[i]);//本征函数 } #pragma omp for//传播损失求解 for(i=0;i tl[i]=TL(vl,la);//传播损失 } } (5)数据收集和输出。 每个节点分配的计算任务完成后,调用MPI_REDUCE函数将计算结果收集到进程0,并将计算结果输出。 基于MPI+OpenMP混合的WKBZ 2维声场并行计算方法,通过在节点间传递消息,节点内共享内存的方式,实现了2维声场“粗粒度+细粒度”的2级并行计算。采用该方法可以将进程数降低到MPI编程模型下的1/NP(NP为单节点计算核心数),在有效提升算法可扩展性的同时,大大降低了进程间的通信次数和通信开销。 利用海军潜艇学院SMP集群系统对WKBZ简正波模型混合并行算法进行测试,该平台共314个计算节点,理论峰值计算能力310 TFLOPS,具体配置如表1所示。 本文分别将MPI、MPI+OpenMP混合编程模型实现的2维WKBZ简正波模型并行计算程序,使用同样的计算资源进行性能测试和分析。为科学地表达2种编程模型的计算性能的差异,测试过程中按如下原则设定进程数和线程数: Table 1 SMP cluster configuration table表1 SMP集群配置表 (1)在MPI编程模型中,指定单个计算核心只运行1个进程,单节点进程数与核心数相等。 (2)在OpenMP编程模型中,指定单个计算核心只运行1个线程,单节点线程数与核心数相等。 (3)在MPI+OpenMP混合编程模型中,单节点只启动1个进程,节点内线程数与核心数相等。 上述3个原则保证了计算过程中单个物理核心只运行1个计算任务。为便于比较,将计算资源统一用核心数进行表示,即在MPI编程模型下,核心数=进程数;在MPI+OpenMP混合编程模型下,核心数=进程数*单节点核心数。 利用图5给出的深海声道行声速剖面,设定计算频率为5 000 Hz,表2为MPI与MPI+OpenMP 2种编程模型实现的水声传播模型的计算时间,图6为其对应的加速比。 Figure 5 Typical deep ocean sound speed profile图5 典型深海声速剖面 Table 2 Computing time of MPI andMPI+OpenMP hybrid parallel programs 编程模型核心数244896192384768MPI+OpenMP3.421.790.940.680.530.43MPI2.481.401.021.262.434.55 Figure 6 Parallel speedup of MPI and MPI+OpenMP parallel programs图6 MPI与MPI+OpenMP并行程序计算加速比 由表2和图6可以看出: (1)使用单计算节点运行时(24核),MPI编程模型程序性能优于MPI+OpenMP混合编程模型的,这主要是由于在利用OpenMP对break、continue等语句进行处理时引入了一定的额外计算量引起的。 (2)对于MPI+OpenMP编程模型,计算时间随核心数的增加逐渐减小,最小运行时间为0.43 s,核心数超过96个后,计算时间的减少量逐渐减小。 (3)对于MPI编程模型,计算时间随核心数的增减呈现先减小后增加的现象,最小运行时间为1.02 s,核心数超过96个后,计算时间随核心数的增加线性增加。 为了进一步分析造成2种编程模型性能差异的原因,将2种编程模型的运行时间分为并行计算时间和进程间通信时间2部分进行了测试,测试结果分别如表3和表4所示。 Table 3 Computing time of MPI parallel program表3 MPI并行程序计算时间 s 表3为MPI并行程序计算时间表,图7为其计算时间图。从表3和图7可以看出,随着核心数的增加,MPI程序并行部分计算花费时间由2.29 s减少为0.11 s,占总计算时间百分比由92.3%降低至2.4%;进程间通信消耗的时间由0.21 s增加至4.44 s,占总计算时间的百分比由7.7%提高至97.6%,从而导致并行程序的计算效率大幅降低。 Figure 7 Computing time of MPI parallel program图7 MPI并行程序计算时间组成图 Table 4 Computing time ofMPI+OpenMP parallel program 时间核心数244896192384768并行计算时间3.101.630.780.420.200.13进程通信时间0.320.160.160.260.330.30合计3.421.790.940.680.530.43 Figure 8 Computing time of MPI+OpenMP parallel program图8 MPI+OpenMP混合并行程序计算时间 表4为OpenMP+MPI并行程序计算时间表,图8为其计算时间图。从表4和图8可以看出,随着计算规模的增加,MPI+OpenMP程序并行计算部分花费时间由3.10 s减少为0.13 s,占总计算时间百分比由90.6%降低到73.4%;进程通信部分消耗的时间由0.04 s增加到0.46 s,占总计算时间由9.4%提高至26.6%。 从上面的分析可以得出以下结论: (1)2种编程模型:并行计算部分花费的时间随核心数的增加大幅减少,单核心计算时间基本一致。 (2)MPI并行程序:进程通信消耗的时间随核心数的增加呈现先减少后增加的现象,且随核心数的增加,逐渐在整个运行时间中占主导地位,远大于并行计算部分花费的时间。 (3)MPI+OpenMP并行程序:通信时间虽然也呈现先减少后增加的现象,但由于进程的数量远远小于MPI并行程序的数量,其通信时间较MPI程序能够降低1个数量级,具有更高的计算性能和可扩展性。 综上,MPI+OpenMP混合编程模型通过节点内共享内存、节点间传递消息的方式,大大减少了进程通信消耗时间,计算性能和可扩展性远高于MPI编程模型。因此,对于实时计算问题的并行处理,必须采取合理的通信方式,尽可能降低由于进程间通信带来的时间开销,提高程序的执行速度,MPI+OpenMP混合编程是解决此类问题的1个很好的选择。 本文基于SMP集群,采用MPI+OpenMP混合并行编程模型,实现了WKBZ简正波模型的2级混合并行计算。该方法大大减少了进程间频繁通信引起的时间开销,同单一的MPI编程模型相比,具有更高的计算性能,基本满足水下声场信息实时仿真的需求,对具有2级循环结构应用问题的并行处理具有较好的参考价值。4 算法测试与结果分析
4.1 测试环境
4.2 测试方法

4.3 测试结果

表2 MPI与MPI+OpenMP混合并行程序计算时间s
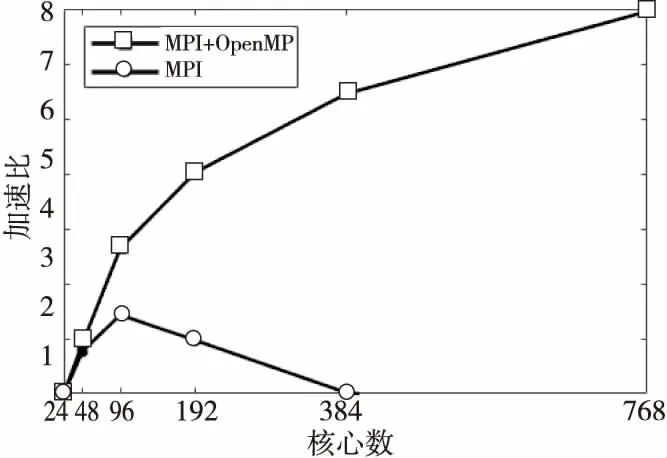
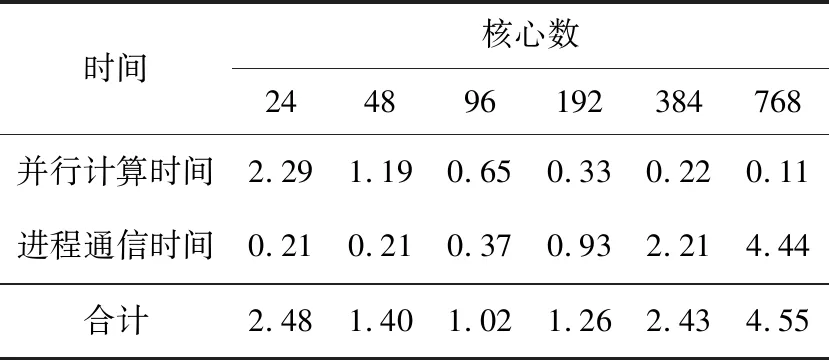

表4 MPI+OpenMP并行程序计算时间s

5 结束语

