神经网络结合直接数字合成技术的电力系统谐波测量方法
宫元九,周佳禾
(辽宁大学信息学院,辽宁沈阳 110036)
0 引言
电力系统的谐波源于电力电子装置中的非线性负荷,如变频调速器、大功率开关电源等。电网中产生的高次谐波影响电网的供电质量,也能影响电网中其他设备的正常运行。作为谐波分析的一个分支,谐波测量也是电力电测仪表的重要功能之一。
谐波测量技术的发展,经历了模拟式、数字式到智能化的发展过程。早期出现谐波测量方法主要有基于模拟滤波器的谐波测量方法及受限于三相三线制电路的、基于瞬时无功功率的p-q法和ip-iq法。进入到数字化阶段以后,随着单片机与DSP的应用,相继出现了基于离散傅里叶变换(DFT)频域分析方法和基于小波变换(WT)[1-2]及线性调频z变换(CZT)等时频域分析方法。凭借复杂度低的优势,快速傅里叶变化(FFT)逐渐占据了谐波测量的主导地位。使用FFT测量谐波需要锁相环[3]的硬件支撑,以适应电网频率的波动。如果无法实现同步采样,采用时域插值修改等效采样频率或采用时域加窗结合频域插值的方法,可以适度改善测量精度,无法在根本上解决问题。
作为传统机器学习技术代表之一,神经网络技术广泛应用于工业测量[4-5]与控制[6]等领域。神经网络技术为电力谐波测量提供了一种不同的解决方案,其独特的优势在于不受同步采样的限制。用于谐波测量的神经网络在结构上可以分为3种类型,即反向传播神经网络[7-10](BPN)、径向基函数神经网络[11](RBFNN)和自适应线性神经网络[12-14](Adaline)。其中,Adaline的网络结构通常为两层前馈网络,有时为了测量电网频率会增加一个单一节点的输入层。不同于BPN与RBFNN,Adaline测量谐波只有单一的训练环节,当网络收敛时,连接隐藏层与输出层的突触权值即为待测的基波和谐波成分。基于神经网络的谐波测量方法,直接应用了机器学习的成果,具有较好的测量精度,但计算量大、迭代时间长。
本文在Adaline的基础上,设计一种结合直接数字频率合成(direct digital synthesis,DDS)技术的谐波测量实现方法,在确保测量精度的前提下,提升测量的实时性。
1 Adaline的谐波测量原理
对于最高谐波次数为N的交流电压或电流信号,使用固定采样频率获得的采样序列一般可以表示为
(1)
式中:yk为第k个采样值;N为最高谐波次数;fl为电网频率;fs为采样频率;a0为采样序列中的平均值成分;An为基波或谐波成分的振幅;φn为基波或谐波成分的初相;σk为观测噪声。
图1是用于谐波测量的Adaline网络的一种变化结构。附加的虚拟输入节点用于接收采样序列采样值的序号,隐藏层神经元分为2组,神经元数量与待测谐波次数相关,其激活函数为三角函数,输出层是单一的线性神经元。神经网络的输出为
(2)
式中:cos(2πnfk/fs)与sin(2πnfk/fs)表示隐藏层神经元的输出;an及bn为连接隐藏层神经元与输出神经元的突触权值;yk为网络的输出。
网络中的参数f、a0、an及bn均可通过学习获得。当网络收敛时,网络的参数an及bn即为待求基波及谐波成分的正交分量。对比式(1)与式(2)可知,网络的输出是对采样序列的估计,如果观测噪声为独立同分布的高斯噪声,则网络的输出是采样序列的极大似然估计。
训练图1所示的网络,一般采用串行模式,网络中各待学习参数的梯度分别为

(3)

(4)

(5)
(6)
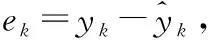

图1 Adaline网络结构图
选用恰当的学习策略,设置合适的学习率[15]并确保网络收敛,图1所示的神经网络可以得到较佳的测量结果。然而,神经网络网络训练过程中浮点运算特别是三角函数的计算量过大,制约了神经网络技术在电力仪表中的应用。
2 结合DDS的神经网络训练方案
2.1 DDS原理
DDS是数字硬件系统中广泛使用的频率合成技术,其主要构成包括相位累加器、正弦查找表及D/A转换器。相位累加器的输出经截断后,利用其高位寻址查找表,查找表中保存有一个周期的正弦幅值数据,利用查找表完成相位到幅值的转换,该幅值数据最终经D/A转换器输出并转化为连续的正弦波信号。DDS技术具有较高的频率分辨率以及同工作时钟一致的稳定度,其输出频率为
(7)
式中:A为累加器位宽;fc为累加器工作时钟;Wf为频率控制字;fOUT为DDS输出信号频率。
2.2 软件DDS
DDS技术提供了一种利用软件模拟DDS生成正弦与余弦函数值的思路。各一个周期的正弦与余弦函数值查找表可根据硬件资源状况存放于代码空间或数据空间,而相位累加器可以简单地用无符号整形实现。软件DDS生成正弦与余弦函数值的方法所需的硬件资源与普通查表法相近,但性能却与DDS相同,且所需计算量极小。以32位无符号长整型实现相位累加器为例,对于任意待求的正弦或余弦函数值,其频率控制字与查找表地址分别为
(8)
(9)
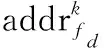
软件DDS的优势在于,输出数据的精度只与查找表的数据类型相关,不存在D/A转换器带来的量化噪声。然而,软件DDS仍然无法摆脱DDS相位截断的影响。相位截断导致软件DDS的输出在数值上存在与实际正弦或余弦函数值的偏差,在频谱上则表现为相位噪声。使用软件DDS,需均衡数值精度要求与硬件资源条件,合理选择相位截断长度。图2所示的频谱图为软件DDS生成的50.2 Hz基波的19次谐波信号的频谱,软件DDS使用的相位累加器为32位无符号长整型,截断长度为11位,查找表数据类型为32位浮点型。由图2可知,在截断长度为11位时,软件DDS输出信号的无杂散动态范围(spurious free dynamic range,SFDR)已经优于60 dB。

图2 软件DDS输出单频信号频谱
2.3 神经网络结合软件DDS的谐波测量仿真
图3为利用图1的神经网络结合软件DDS实现谐波测量的MATLAB仿真结果。软件DDS相位累加器为32位无符号长整型,查找表数据类型为32位浮点型,截断长度为11位,频率分辨率可达7.45×10-8Hz。仿真所用采样序列为
(10)
式中:yk为采样序列的第k个采样值;fl=50.2 Hz为仿真的电网频率;fs=3.2 kHz为采样频率;φ1及φn分别是基波及谐波的初相,为-π/2~π/2之间的随机值;σk为附加的高斯噪声。
维持采样序列50 dB的信噪比。采样序列长度为80,包含了基波的2~19次谐波,各次谐波的谐波含有率均为2%。

(a)频率学习曲线

(b)误差能量变化曲线
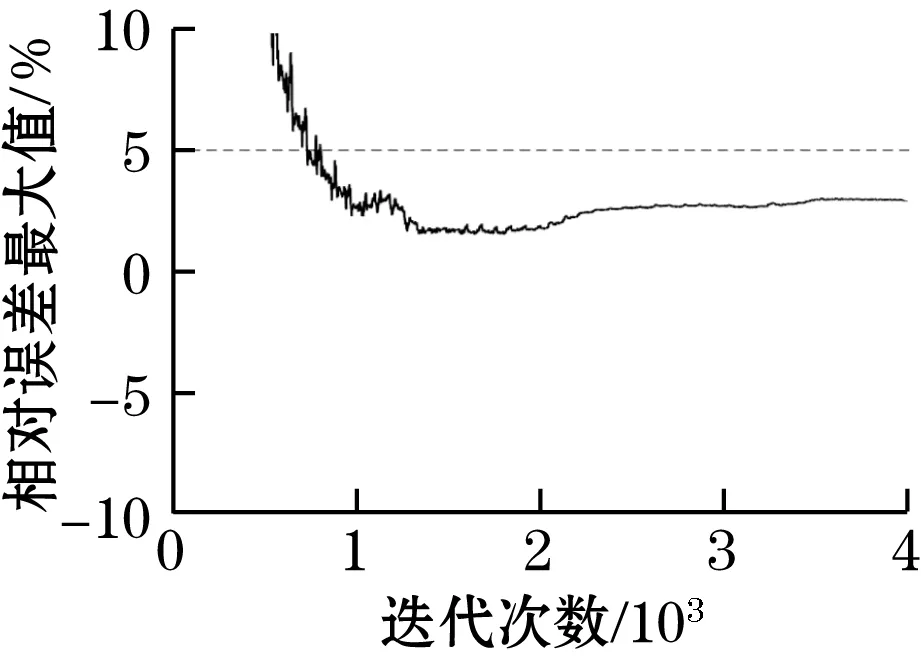
(c)测量误差最大值变化曲线

(d)谐波测量误差
神经网络隐藏层共计38个神经元,对应基波及其2~19次谐波。神经网络训练使用串行模式,应用梯度下降法可以得到神经网络突触权值参数a0、an及bn的更新规则:
(11)
(12)
(13)
α(m)=5.0×10-2×(1-0.9×m/50)
(14)
式中:α(m)为第m回合训练时突触权值参数的学习率,随训练逐回合线性下降。
频率参数f使用了与突触权值参数不同的更新规则
(15)
(16)
β(m)=1.0×10-6×(1-0.8×m/50)
(17)
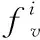
初始条件方面,突触权值a0、an及bn的初始值均设为0.0,动量项fv的初始值为0.0 Hz,频率参数f的初始值为50.0 Hz,采用顺序抽样的方式训练50个回合。图3给出了相关的学习曲线与仿真测量结果。图3(a)是频率参数的学习曲线及其最终测量结果,从中可以明显看出限幅对训练早期的影响;图3(b)中的实线是每回合误差能量平均值的变化曲线;图3(c)是训练过程中各次谐波估计相对误差绝对值中最大值的变化曲线;图3(d)给出了网络训练结束时的测量误差,包括了单次仿真结果的相对误差及10次仿真结果方均根值的相对误差。结合图3(a)~图3(c)可以看出,在该次仿真中经过20个回合左右的训练,网络趋于收敛,测量误差可以满足GB/T 14549的要求。
需说明的是,在电网频率未知条件下的仿真,随机初相及附加的噪声使得每次仿真训练的收敛过程不相同。但大量的仿真结果表明,50个回合的训练足以确保网络收敛并满足谐波测量精度的要求。
图3(b)中虚线是在频率参数f已知但与采样序列仿真频率存在最大2.0×10-4的相对偏差时,误差能量平均值的变化曲线。可以明显地看出,在其他条件相同的情况下,如果频率参数已知,经过5个回合左右的训练,网络即趋于收敛,收敛速度明显加快。这说明,通过其他方式测量电网频率,不仅可以减少网络训练时频率参数更新的计算量,而且提高了网络训练的收敛速度,对谐波测量实时性的提升作用明显。
3 实验结果与分析
在dsPIC33EP64与ATT7022C为核心的电力仪表平台上对比神经网络结合DDS测量谐波的不同实现方法,进一步验证其实时性和测量精度。
ATT7022C是三相电能专用计量芯片,适用于三相三线和三相四线应用。根据配置,ATT7022C能够以3.2 kHz采样频率及16 bit的分辨率对电压或电流进行单通道、双通道或三通道采样,并将采样数据保存于片上长度为240的缓存存储区中。ATT7022C具有较高的电网频率测量精度,其频率测量数据经过dsPIC33EP64进一步处理后,测量误差小于0.01 Hz。
在该硬件平台上,使用仿真阶段所用的神经网络,对比训练的3种实现方法,即利用库函数计算三角函数值的网络训练方法、利用软件DDS生成三角函数值的网络训练方法和软件DDS结合Q15、Q15.16定点格式的网络训练方法。在方法2中,软件DDS相位累加器为32位无符号长整型,查找表置于代码空间,其长度为2 048,数据类型为32位浮点型。方法3与方法2的不同之处在于,查找表的数据类型为Q15,而其他浮点类型的变量均调整为Q15.16。
使用长度为80的采样序列,训练5个回合。表1给出了3种实现方法的耗时。前两种实现方法的对比可以看出,软件DDS对提升测量实时性作用显著。后两种实现方法之间的差异则是意料之中的,但采用定点格式也带来了代码编写与维护的压力。

表1 不同实现方法耗时 ms
在该仪表平台上,使用方法3在电流谐波含有率分别为1%、2%及5%等3种条件下进行实际谐波含有率测量。所用信号源为TH-0301三相交直流指示仪表校验装置,测量采用的基波频率为49.5 Hz,电流有效值为1 A。对于待测的电流通道,使用长度为80的采样序列,谐波次数为2~19,每次测量训练5个回合。仪表经过标定后,将原始测量数据经长度为10的滑动平均值滤波器处理作为最终的测量结果。表2所示为3种不同谐波含有率条件下的实际测量结果,测量精度完全满足GB/T 14549的要求。
利用表2中的数据并结合ATT7022C的电流有效值测量结果,可以换算各次谐波的有效值:
(18)


表2 谐波含有率测量结果 %
进一步的实验结果表明,通道的改变、电量类型的差异、电网频率在49.5 Hz与50.5 Hz之间变化等因素对测量结果的影响均远远小于表2所示的测量误差,表现出良好的一致性。
4 结束语
神经网络结合软件DDS与定点格式运算可以保证在电力仪表中谐波测量的实时性,对于感兴趣的、已知的谐波成分能够提供满意的测量精度。这种方法也可以扩展应用于频率已知的间谐波测量。Adaline的网络结构与其频率测量能力密切相关,对于存在但与网络结构无关的频率成分,Adaline无能为力。应对这种情况,FFT与Adaline神经网络的联合是可供选择的手段之一。FFT负责分析采样序列中存在的频率成分,进行粗测,Adaline神经网络则根据已知的频率成分构建相应的网络结构,最终完成对已知频率的精确测量。

