声学CT温度场重建系统的收发器位置优化与实现

颜 华，张力男

(沈阳工业大学信息科学与工程学院，辽宁沈阳 110870)

0 引言

声学CT温度场重建技术根据在被测区域周围布置的收发器之间的声波传播时间，推算被测区域温度分布，具有非接触不破坏温度场、测温范围广、环境适应能力强等优点，是温度场测量领域的研究热点。工业锅炉的温度分布监测是此技术的典型应用[1-2]。利用该技术监测深海热液口温度分布[3]、大气温度分布[4]、仓储粮食温度分布[5]、堆积物料的温度分布[6]等方面的研究也正在开展。

声波收发器的布局不同，声波传播路径与覆盖区域也不同，进而对温度场重建结果产生影响[7-8]。因此有必要对收发器的位置进行优化。文献[9]以双峰对称温度场模型重建误差(均方根误差)最小为目标，对8声波收发器的位置进行优化，仿真重建结果表明与普遍采用的均匀布置相比，优化布局下的双峰对称温度场模型重建均方根误差有明显改善。

被测区域的温度分布通常会呈现出多种多样的特征。例如炉膛内的温度场模型大致有以下3种情况：燃烧正常时的单峰对称温度场模型；火焰直接冲刷水冷壁管时的单峰偏置温度场模型；由于吹入的煤粉分布不均匀，燃烧状况不佳，火焰出现多个峰值时的多峰温度场模型[10]。与工业炉温度场相比，储粮温度场中可能出现的热点(峰值)数目更多，热点位置的随机性也更强[11]。因此收发器布局优化时必须考虑对特征各异的温度分布的普适性问题。

为提高收发器布局对被测区域内可能出现的特征不同的温度分布的适应性，本文提出一种声波收发器位置优化新方法：以均匀温度场重建误差最小为目标，用粒子群优化算法优化收发器位置坐标。为验证所提方法的有效性，采用基于均匀温度场的优化布局(本文方法)、基于双峰对称温度场的优化布局(文献[9]方法)和常用的均匀布局，对单峰偏置等5种温度场模型进行了仿真重建。重建结果表明本文所提方法对应的重建误差总体上显著优于另外两种。采用声学CT温度场重建系统和本文方法确定的收发器布局，对用电热器形成的单峰偏置温度场进行了重建实验。重建结果进一步验证了本文方法确定的收发器布局的有效性和实用性。

1 声学CT温度场重建原理

声波在气体介质中的传播速度c(m/s)、气体介质的热力学绝对温度T(K)和由气体组成决定的常数z(对空气而言其值为20.045)之间的关系可表示为[11-12 ]

(1)

为测量某一区域的温度分布，需将该被测区域划分成M个像素(网格)，并在被测区域周围设置若干声波收发器，形成N条有效穿越被测区域的声波路径。用适当的重建算法，可由测量或仿真计算得到的N条有效路径上的声波传播时间，重建出被测区域的声速分布，进而利用式(1)得到温度分布。

本文针对二维温度场即典型层面的温度场重建进行研究，给出的重建结果都是采用MTR算法获得的[11-12]。对于二维温度场，MTR算法可简述如下。

假设被测层面上声速的倒数分布为f(x,y)，则声波沿路径lk的传播时间tk可表示为

(2)

将f(x,y)表示为M个Markov径向基函数的线性组合：

(3)

式中：xi、yi为第i个网格中心的坐标;εi为待定系数；φi为 中心位于(xi，yi)的径向基函数;α(α>0)为径向基函数的形状参数。

将式(3)带入式(1)可得：

(4)

定义A=(aki)k=1,…,M,i=1,…,N,ε=(ε1,…,εM)T，t=(t1,…,tN)T，可得：

Aε=t

(5)

式(5)的Tikhonov正则化解可以表示为

(6)

其中σ1≥σ2≥…≥σp>0是矩阵A的奇异值，p是非零奇异值总数，uj和vj分别为矩阵A的左、右奇异值向量；μ是正则化参数。用仿真计算或实际测量的方法获得声波传播时间向量t以后，可由式(6)确定参数向量ε；进而通过式(3)、式(1)得到被测区域的温度分布。

重建温度场的质量可以采用最大相对误差emax、平均相对误差eave、均方根误差erms和热点温度误差eh来评价。计算公式如下：

(7)

(8)

(9)

(10)

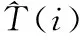
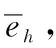
2 收发器位置优化

2.1 优化参数

对于二维温度场重建来说，一个由NS形成的收发器阵列有2NS个坐标参数要优化。但如果收发器是固定在一个预先制作好的支架上，则NS个收发器的位置可由NS参数描述，本文就是这种情况，NS=8，有8个待优化参数。

2.2 目标函数

用系统实际运行时拟采用的温度场重建算法，本文是MTR算法，对均匀温度场(温度在被测温度范围内)进行仿真重建，并以重建温度场平均相对误差eave最小为目标函数。

2.3 优化方法及优化结果

优化方法采用粒子群优化(particle swarm optimization，PSO)算法[13-15]。

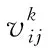
(11)

式中：ω为惯性权重；c1、c2为正的加速度常数；r1、r2为0～1之间均匀分布的随机数。

其中，ω代表粒子对当前速度的承袭度；c1和c2调节学习最大步长，r1和r2用来增加搜索的随机性。c1和r1、c2和r2分别决定了粒子自身学习能力和向群体中优秀个体学习的能力。满足搜索终止条件时找到的全局最优位置，就是寻到的最优解。

粒子群算法的性能很大程度上取决于算法的控制参数。惯性权重是PSO算法中最重要的可调参数。较大的ω有利于跳出局部极小值，便于全局搜索，而较小的ω会增强算法的局部搜索能力，利于算法收敛。为了提高局部搜索和全局搜索能力，防止在最优点附近振荡或早熟陷入局部极值的情况，本文采用随机权重法[14-15]确定ω。计算公式如下：

(12)

式中：μmaxμmin分别为随机权重的最大值和最小值；rand(0,1)是0到1的均匀分布。

如果在进化初期就已经在最优点附近，随机ω可能产生相对小的权重值，加快算法的收敛速度；如果在进化初期找不到最优点或在进化过程中陷入局部极值，随机ω可能产生相对大的权重值而最终跳出局部最优。

粒子数的多少依问题的复杂程度而定，粒子数量越多搜索范围越大，越容易找到全局最优解，但是程序运行时间越长。声波收发器位置优化是离线进行的，对运行时间无要求。考虑到问题的复杂性，本文的粒子数取200。粒子的维度也就是问题解的维度。本文是对安装在正方形支架上的8个收发器位置优化，每个收发器的位置可用一个参数描述，所以粒子维度为8。一般c1=c2且取值通常在0到4之间，本文取c1=c2=1.194 5。粒子群搜索的终止条件一般设置为达到预设的最大迭代次数或搜索到的最优位置满足预定最小适应度阈值。本文采用的是最大迭代次数200次。

图1给出搜索过程中重建温度场平均相对误差(即适应度)随迭代次数变化的情况。可以看出迭代到100次时平均相对误差已趋于稳定，此时的平均相对误差约为0.007%。图2给出了本文方法基于均匀温度场优化所确定的8声波收发器布局。作为比较，图3给出了普遍采用的均匀布局。图4给出了基于双峰对称温度场优化，即文献[9]方法，所确定的收发器布局。图2～图4中还给出了这些布局所对应的的声波传播路径和被测区域的网格划分。3种方法声线分别穿过302个网格、293个网格、281个网格。由此可见本文方法优化后的收发器布局所形成的声线能更好的覆盖被测区域。

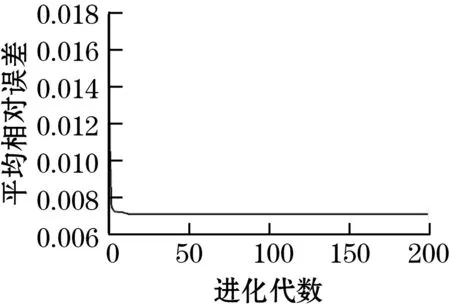
图1 平均相对误差变化曲线

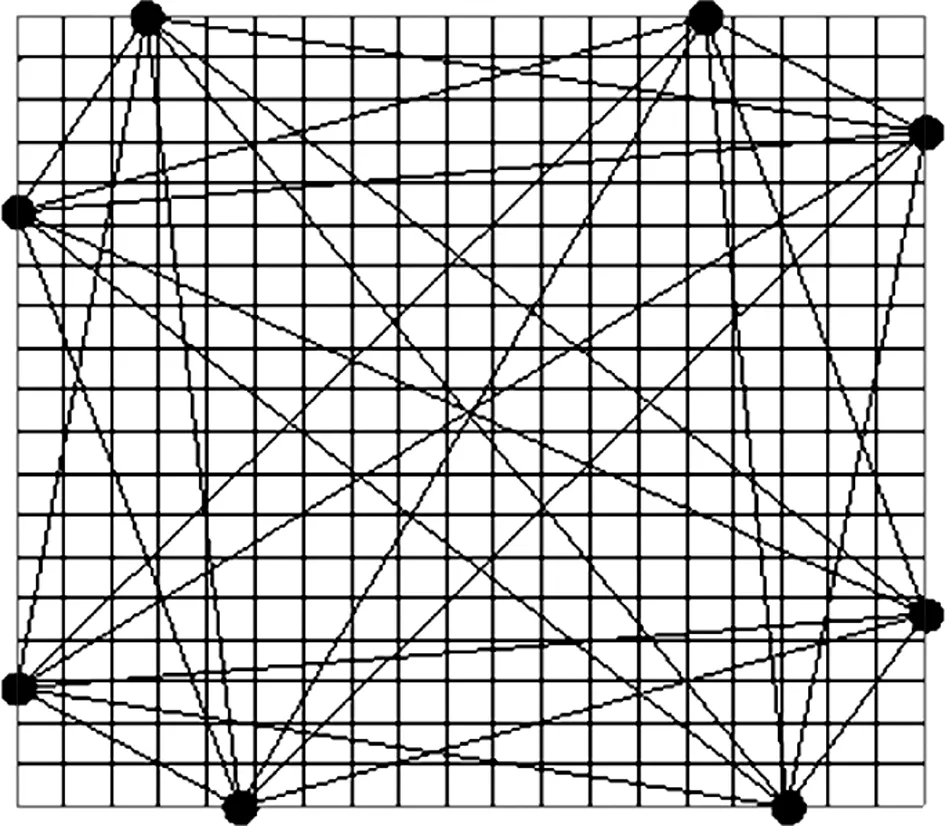
图2 优化布局(本文方法)

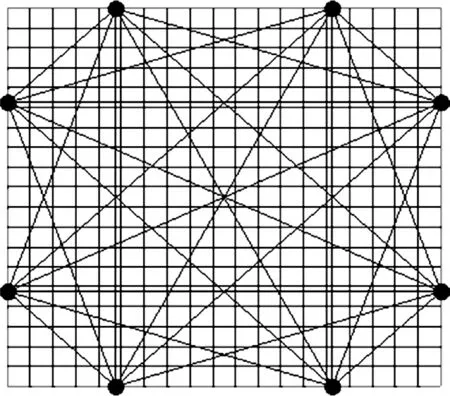
图3 传统均匀布局

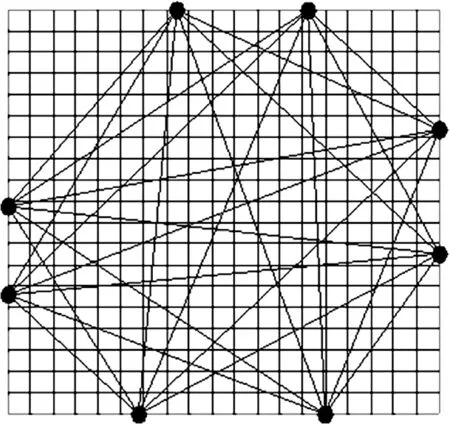
图4 优化布局(文献[9]方法)

3 优化效果验证

3.1 仿真重建

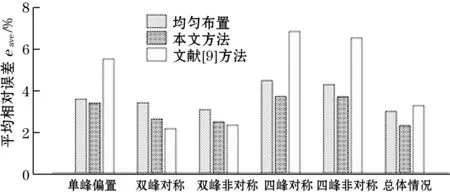
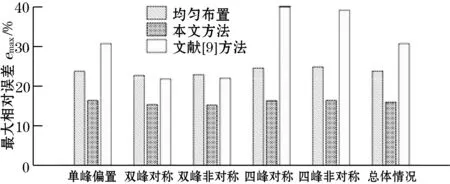
为了验证本文所提声波收发器位置优化方法的有效性，采用本文方法得到的优化布局、文献[9]方法得到的优化布局和常用的均匀布局，对单峰偏置、双峰对称、双峰非对称、四峰对称、四峰非对称5种温度场模型进行了仿真重建。图5给出了模型温度场以及不同布局所对应的重建温度场。由于重建温度场采用了与模型温度场相同的颜色条，故省略了重建温度场的颜色条。图6给出了不同收发器布局对应的重建误差比较，其中总体情况是5种温度场重建误差的平均值。由图5、图6可以看出：

(1)对于单峰、双峰温度场模型，3种收发器布局都能正确地重建出温度场模型的特征；但对于复杂的四峰温度场模型，文献[9]方法的重建温度场图像有明显失真。

(3)总体来看与优化前相比，本文方法的各项重建误差指标均有改善，最大相对误差的改善最明显；而文献[9]方法只是对双峰温度场模型的重建误差指标有改善，非双峰温度场模型的重建质量尚不及优化前。

综上，本文方法确定的优化布局重建质量最佳，对特征各异的温度场模型适应性最好。最大相对误差、平均相对误差、均方根误差热点温度误差分别降低至优化前的67.0%、77.3%、83.8%、78.5%。

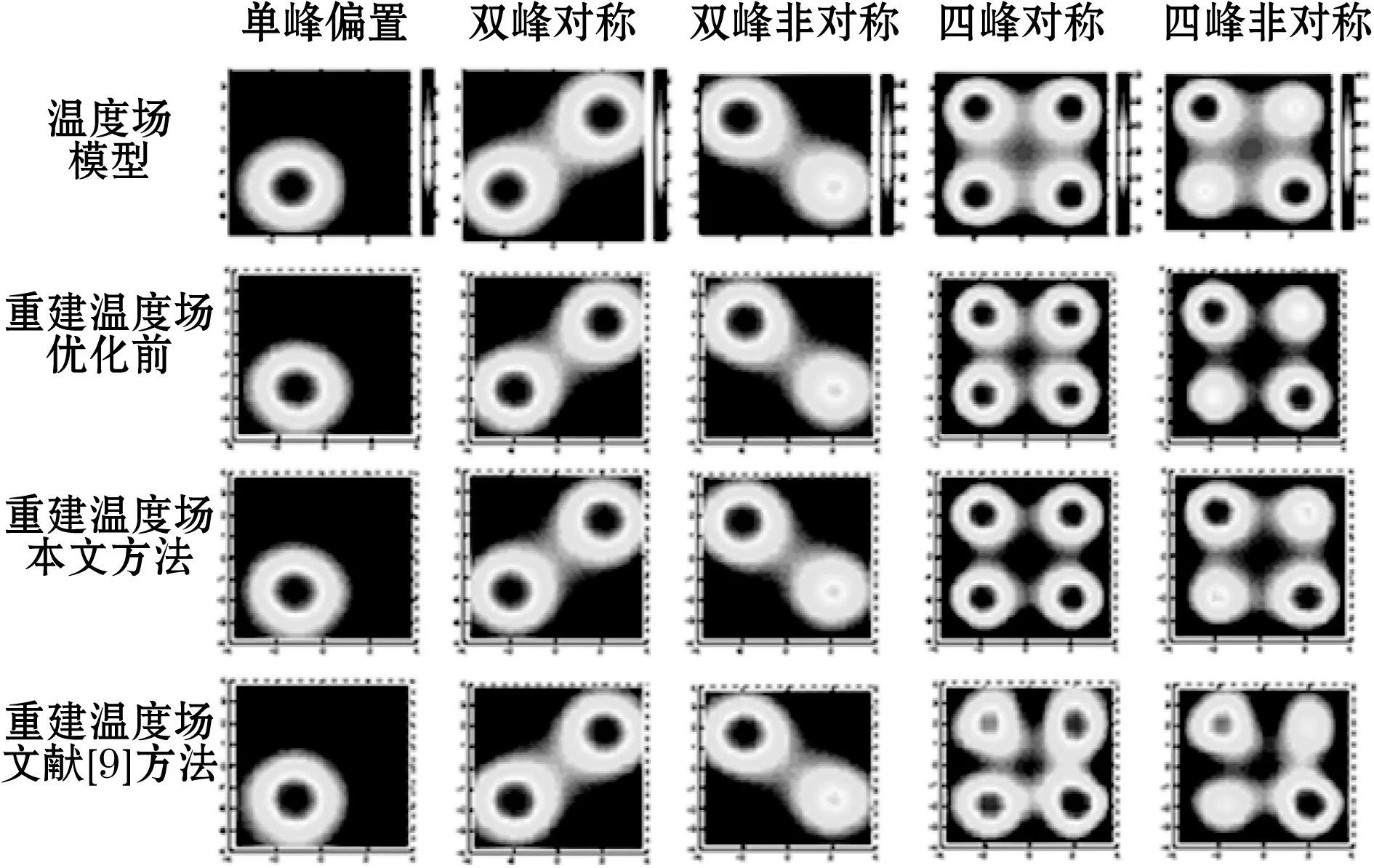
图5 温度场模型及3种收发器布局所对应的重建温度场

3.2 实验验证

将8声波收发器按照本文方法得到的优化布局进行了实际安装，如图7所示。8个声波收发器围成了一个130 cm×130 cm的正方形被测区域。在被测层面的下方放置一个电热器，电热器通电后在被测层面上形成一个单峰偏置温度场。实验是在室温为26 ℃时进行的。运行基于虚拟仪器的声学CT温度场重建系统，可以实时重建出被测层面的温度分布。图8给出了通电5 min后的重建温度场，此时系统给出的被测区域最高温度是33.1 ℃。利用FLUKE 54Ⅱ温度计测量到的被测层面最高温度是33.3 ℃。实验结果进一步验证了本文方法确定的收发器布局的有效性和实用性。

图7 实际收发器布局

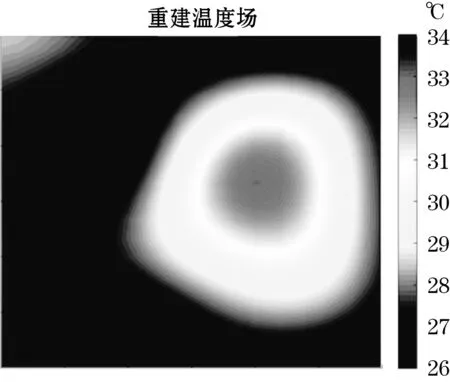
图8 重建的温度分布

4 结论

本文提出一种声波收发器位置优化新方法：以均匀温度场平均相对误差最小为目标函数，用粒子群优化算法优化收发器位置坐标。单峰偏置等5种典型温度场模型仿真重建结果表明：与传统的均匀布置相比，本文方法的各项重建误差指标均有明显降低。采用本文方法获得的优化布局，对用电热器形成的单峰偏置温度场进行了重建实验，实验结果进一步验证了所提方法的有效性和实用性。

针对某种或某几种典型分布进行传感器优化是CT技术中的常用方法。但这样优化的传感器对于优化时未被考虑的分布通常对应着较大的重建误差。本文所提方法针对均匀温度场进行位置优化，由于被测区域内温度分布上无差异，所以优化布局的声波传播路径对被测区域的采样有更好的均衡性，并最终体现在重建误差的明显降低上。