柔体大变形参数的光纤光栅集成检测方法

吕宇翔，任 旭，路长厚，李学勇，马晓源，谷雨橦

(山东大学机械工程学院，山东济南 250061)

0 引言

传统机器人的结构刚性限制了运动灵活性，对环境的适应能力低，只能在结构化环境中工作，人机交互安全系数低。这些缺点制约了刚性机器人的发展应用，研究者以软体动物为原型，提出了软体机器人[1-2]，也称柔性机器人。柔性机器人由可承受大应变的柔体材料加工而成，理论上具有无限自由度和分布式连续变形能力，同时其自身良好的柔性和安全性等弥补了刚性机器人的不足，在工业生产、科学探测等领域具有广泛的应用前景。

关于软体机器人的研究多为设计探讨软体机器人运动控制方法，采用开环控制的思路，以视觉的直观方式观测柔体变形，然而软体机器人很多情况下需要深入狭小的环境工作，难以直接观测，软体机器人的运动控制主要依靠自身柔体运动稳定性，无法确定变形情况以及是否失稳。因此对软体机器人柔体变形过程的监控检测具有重要意义，其中对弯曲变形的识别检测极为关键。但目前来说，对柔体形变信息检测的研究较少。

由于软体机器人具有无限自由度和连续变形能力，大多传统检测方案难以使用，需要新型传感器或检测方法来检测软体机器人形状变化。光纤光栅传感器具有体积小、弯曲性能好、抗电磁干扰、可复用等优点[3]，比较适合作为敏感元件粘贴或埋入柔性机器人表面形成光纤传感网络，实现分布式测量。J.Yi等[4]研究了一种基于正交光纤光栅传感器阵列的框架模型结构空间形状实时感知和三维重建方法，H.Wang等[5]在柔性机械臂埋入分布式光纤布拉格光栅传感器网络设计形状检测算法。R. J. Roesthuis等[6]提出了集成光纤光栅传感器阵列的镍钛合金针样机，测量轴向应变，计算针的曲率，用光纤光栅传感器重建三维针形。王超[7]设计了一种软体机械臂三维形状检测传感网络和方法，基于分段常曲率-挠率假设，将光纤光栅传感网络的测量值转换为节点的空间位置，绘制出软体机械臂的三维形状。

石英光纤布拉格光栅的应变检测量程能达到6 000 με，在以上形状检测重构中，光纤光栅传感器均直接采集所需方向上的应变，结构形变时测量应变较小属于光纤光栅测量量程内。但这种布置方式并不适用于测量大变形的柔体，在柔性机器人工作中时常伴随着柔体的大应变[8](超过2%的应变)，柔体在较大角度弯曲等大变形时，其局部应变远超过光纤光栅测量量程。且平行布置的分布式光纤光栅传感网络无法区分柔体拉伸和扭转状态，无论柔体是纯拉伸还是扭转时，传感网络测得的各点应变均一致，无法有效区分。

文中提出应对柔体大变形的光纤光栅检测方法，可以实现柔体变形大应变检测，同时区分识别柔体弯曲、拉伸、扭转变形参数，完成柔体大变形监控检测。检测过程中采用螺旋倾斜缠绕布置方法，扩大传感设备应变测量范围，采用不同旋向的光纤缠绕方式来区分柔体大变形拉伸、扭转、弯曲状态并进行三维形状重构。

1 检测对象

本文中以目前软体机器人中应用较广泛、研究相对成熟的软体抓取机械臂为检测对象，这类软体机器臂以气液驱动、记忆合金驱动、线驱动等多种形式实现机械臂的弯曲、拉伸变形来达到空间预定位置，由于本体在空间弯曲中也有扭转变形因素，选取圆柱柔体来代表此类软体机械臂，检测柔体大变形过程。

2 柔体大变形检测方法

2.1 光纤光栅传感原理

光纤布拉格光栅是在纤芯上产生周期性的折射率分布而形成。当宽带光波在光纤中传输时，光纤布拉格光栅对入射光中相应频率的光产生相干反射，形成中心反射峰，满足光纤布拉格条件的光将被反射，其余的透射光则不受影响。FBG反射峰的中心波长λB=2neffΛ。neff为FBG反向耦合模的有效折射率，Λ为光栅周期长度。

外界环境的变化引起光纤光栅温度、应变等变化，导致Bragg中心波长发生偏移，通过对中心波长的监测可实现对外界环境参数变化的检测。保持实验过程中温度场恒定，光纤光栅仅受轴向应力作用，应变对中心波长偏移的关系为ΔλB=λB(1-Pe)ε。ΔλB为中心波长偏移量，Pe为光弹系数。由中心波长偏移量可得光纤光栅测量应变εFBG：

(1)

对于常用的石英光纤，Pe取0.216 nm/με。

2.2 大应变测量方案

在圆柱式柔体大变形的测量环境中，为实现大应变检测的目的，采用螺旋倾斜的布置方式避开载体应变变化灵敏方向，弱化光纤光栅应变变化以扩大应变测量范围，如图1所示。

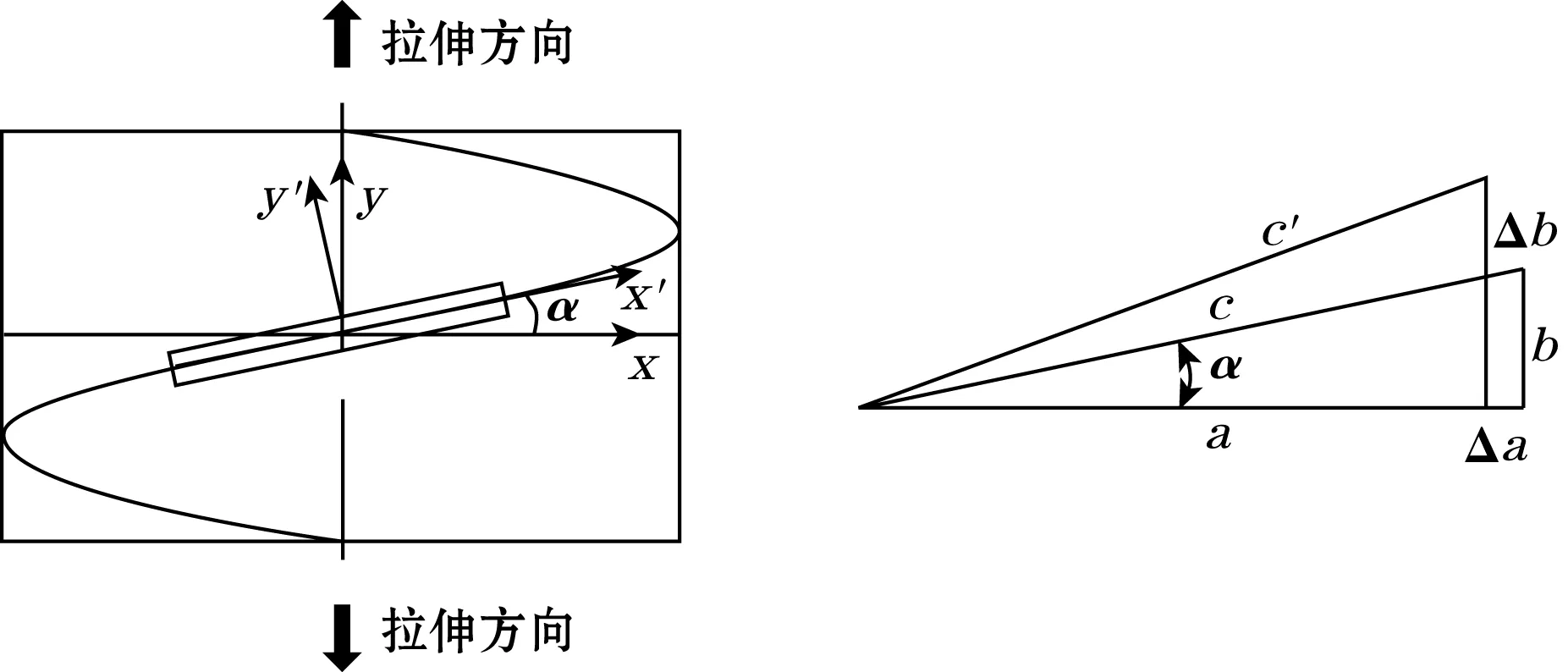
图1 光纤光栅螺旋布置与栅区长度变化

图1中，c为光纤光栅栅区原长，a和b为分解的直角边长度，α为光纤螺旋缠绕时螺旋升角，直角边b的应变为拉伸方向的待测应变ε，斜边c的应变为光纤光栅倾斜布置应变εc，选取适当的螺旋升角获得合适的应变测量范围扩大倍数，以实现大应变检测的目的。推得倾斜布置应变：

(2)

式中v为柔体材料泊松比。

根据图1中xy和x′y′坐标系转换关系，x′轴线方向应变即为光栅测量应变，可简化倾斜布置应变为

εc=ε(sin2α-vcos2α)=kε

(3)

倾斜布置光栅测量的灵敏度降低，角度降敏系数[9]k=(sin2α-vcos2α)大致反映倾斜布置应变与轴向应变的比值。选取不同的螺旋升角α，直接影响实际应变测量范围。

2.3 光纤光栅传感测点布局

为了识别柔体形变中扭转、弯曲、拉伸变形，通过左旋和右旋交错的光纤螺旋缠绕方式，在圆柱截面周向上布置4个光纤光栅测点。同一横截面上4个倾斜应变测点布置见图2。

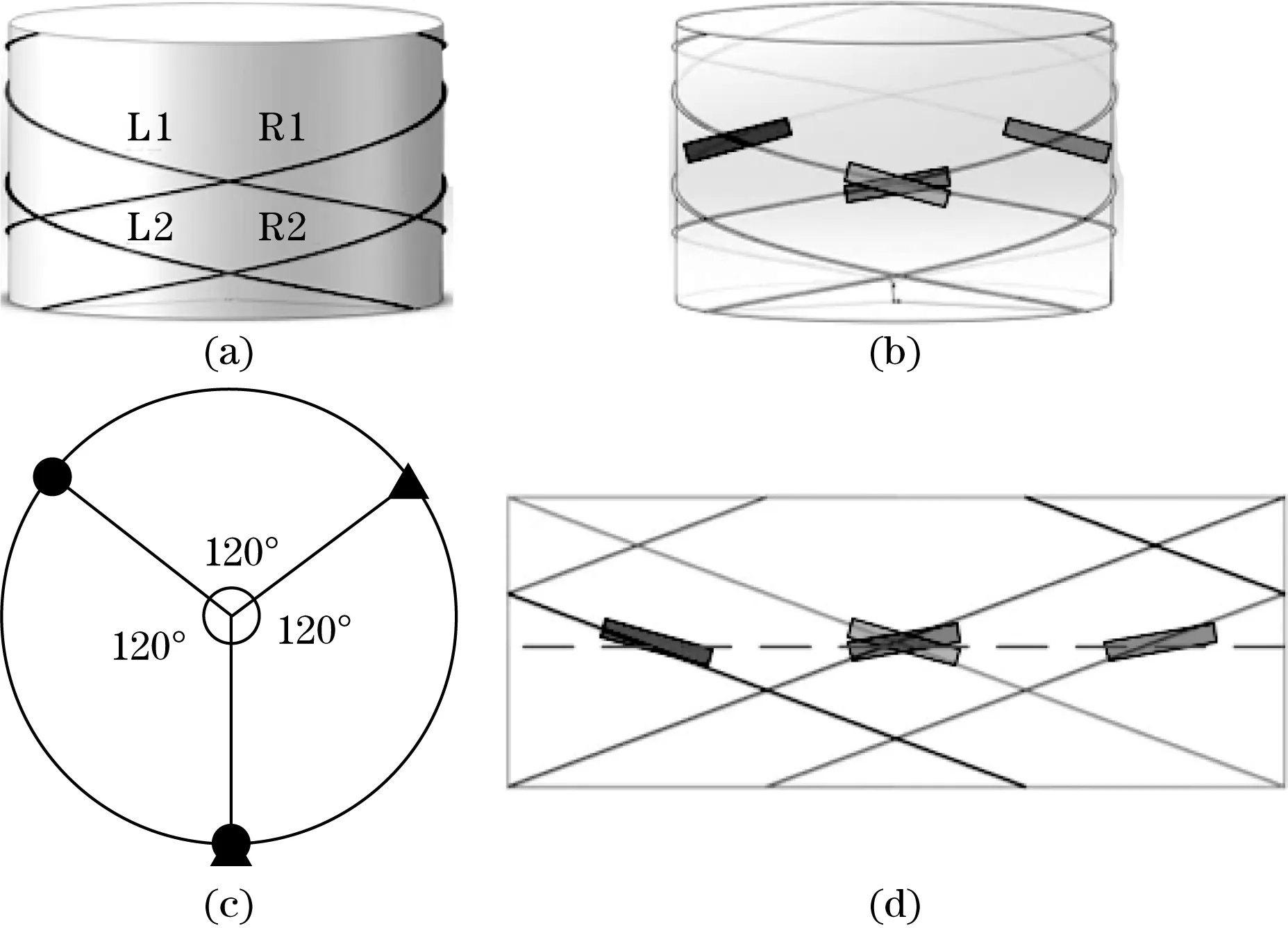
图2 光栅光栅测点布置

在柔体表面缠绕两根左旋光纤L1、L2与两根右旋光纤R1、R2，如图2(a)所示，图2(b)为光栅测点位置，图R1和L1测点交叉重叠，R2、L2分别与R1、L1平行且等间距均布于同一横截面上，图2(c)是测点在截面上投影的位置图，光纤布置沿侧面展开见图2(d)。其中重合测点处栅区长度变化见图3。

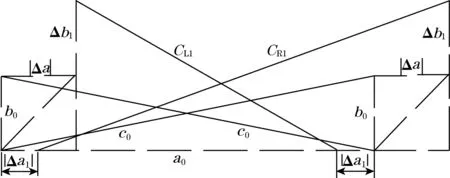
图3 交叉重合测点光栅形变示意

重合测点轴向长度变化一致为Δb1，横向长度变化有扭转引起的变形Δa和轴向拉伸引起的弹性变形Δa1。布置重合测点来区分柔体扭转、拉伸状态参数，柔体扭转变形时，相反旋向的光纤光栅长度变化是不同的；而拉伸变形时，长度变化一致。布置周向不同位置的测点来识别柔体弯曲方向和程度。

利用重合测点处轴向长度变化一致而扭转长度变化相反的特点来分解得到扭转应变，进而解得周向不同位置的轴向应变。4个光纤光栅栅区测量长度为：

(4)

由应变关系将式(4)转化为：

(5)

式中：εa为横向扭转应变；εb1、εb2、εb3为周向等间距分布的轴向应变，可由方程解得。

3 形状重构算法

设计形状重构算法可将光纤光栅测量数据推算得的应变转化为形状参数，反演节点信息重构柔体变形三维形状。

将圆柱柔体划分成n分段，当每段内弧长足够小时，可将每分段变形柔体中心轴线视为空间弯曲圆弧，由外圆周上等间距均布的3条轴线长度，可推算得柱体弯曲情况，将扭转集中在分段接触面上，将分段组合连接重构柔体中心轴线变形形状。其中，第i分段(i=1,2,…,n)内弯曲曲率和偏转方向分析见图4。

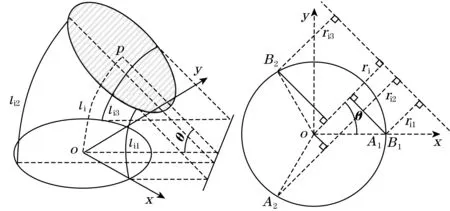
图4 分段弯曲变形示意与参数间关系

由轴向应变得周向等间距分布的分段轴线长lij=l0(1+εbj),j=1、2、3，l0取决于柔体总长度和分段数量。利用弧长l=θr、曲率κ=θl以及图示弧线弯曲半径关系解得分段中心轴线长度li、弯曲曲率κi、偏转角φi：

(6)

分段接触面扭转角φ=εa/πDtanα，分段弯曲角度θi=liκi。各分段建立局部坐标系{xi,yi,zi}，zi轴为中心线在o点切线，xi轴为中心线o点指向交叉测点的主法线，yi轴为中心线在o点副法线。分段内轴长、曲率、偏转、扭转等信息唯一确定分段柔体形变形状和节点Pi坐标。整合各分段局部坐标系，获得统一坐标系下各分段节点位置，连接得到柔体变形轴心曲线，重构柔体变形形状。

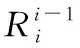
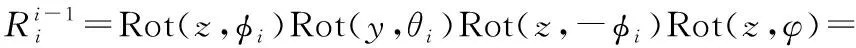
(7)

(8)

(9)

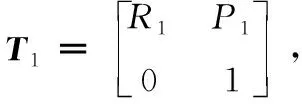
(10)

(11)

由节点全局坐标{Pi}连接得到的柔体中心轴线曲线描述了柔体形变形状。圆柱柔体在受力变形时中心轴线是光顺曲线，具有二阶光滑性，曲率和挠率的变化均匀，没有突变。对于长度相等依次相连的分段，其中心轴线长度li、弯曲曲率κi、偏转角φi、扭转角φi相对于分段在柔体上位置si的曲线变化较均匀，可采用样条拟合插值获取更多的分段数据，计算得到更多的节点位置，描绘出更准确的柔体变形形状中心曲线。

4 实验验证

实验采用直径25 mm、长度500 mm的聚氨酯材质圆柱棒料作为实验柔体，经试验其泊松比为0.4，光纤缠绕方式和测点布置如前所述，螺旋升角为60°。光纤光栅采用胶接方式表贴在棒体表面，连接光纤光栅解调仪输出变形实时反射峰波长并存储。实验平台和光纤光栅粘贴见图5。

图5 实验平台及栅点粘贴情况

实验中固定柔体一端，另一端加力使棒体呈现不同弯曲变形程度。空间弯曲试验通过三维形状比较更直观地展示重构结果，平面弯曲试验通过局部曲率和端点位置的比较更量化地表现出重构算法的精度。

4.1 应变修正标定

柔体待测表面的实际应变经过粘接胶、光纤包层等多层的传递反映到光纤光栅上的应变有所减小[10]，不同粘接胶的厚度、杨氏模量等对应变检测有直接的影响。表面粘贴式光纤光栅测量应变和基体实际应变之间有传递关系，需对光纤光栅测量应变进行标定。

标定时柔体在平面上弯曲，旋转柔体使待标定的光栅栅点位于拉伸外侧，柔体弯曲至固定的弯曲形状，在坐标纸上描绘弯曲轮廓。弯曲至该固定形状保持一段时间后，放松回复原来平直状态，稍后再次弯曲至标定弯曲形状，如此弯曲放松反复多次，记录拉伸时应变测量数据。同理记录不同光纤光栅压缩时应变测量数据。

由描绘的弯曲轮廓线拟合得到弯曲曲线函数求得栅点处实际应变，与测量应变比值作为应变修正系数ka，有ε实际=kaεFBG。处理得R1、L1、R2、L2应变修正系数ka依次为5.54、5.85、5.4、5.4，将修正后应变代回应变方程(5)。

4.2 重构算法过程及结果分析

存储数据通过基于LabVIEW编程的可视化界面输出节点坐标和重构变形曲线。

空间弯曲试验：将竖立柔体朝x轴正方向弯曲一定角度，LabVIEW编程前面板如图6所示，显示节点坐标和重构曲线三维图像。

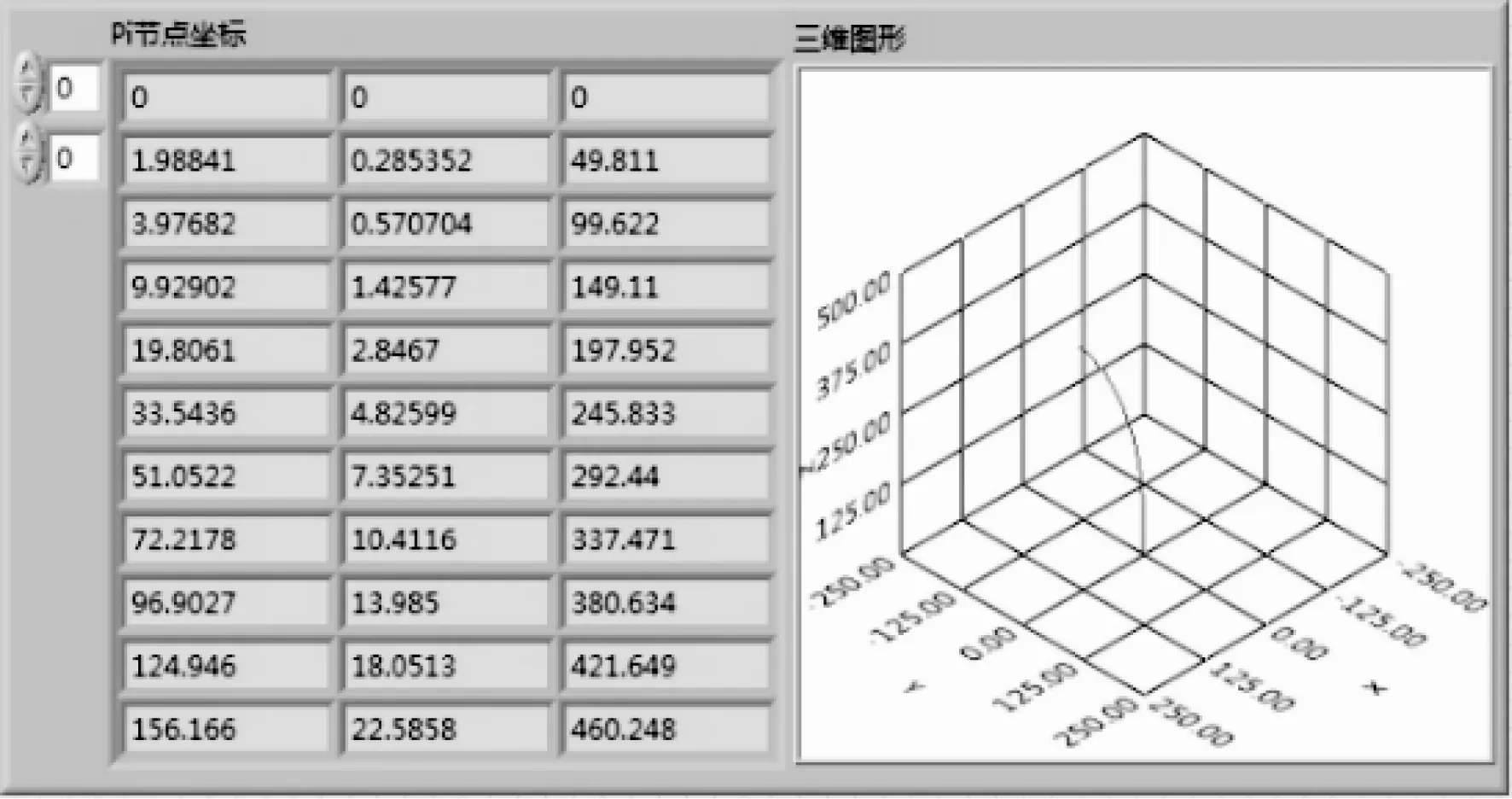
图6 节点坐标及重构弯曲曲线

重构所得的结果形状与柔体实际弯曲形状基本吻合，实际偏转角度约为180°，重构结果为172°，角度计算误差约为4.4%。

平面弯曲试验：将柔体弯曲不同的程度，旋转柔体记录不同的偏转角度，描绘弯曲轮廓并记录测量数据。拟合轮廓得到测点处实际曲率，与修正后的重构曲率和反演端点比较见表1。

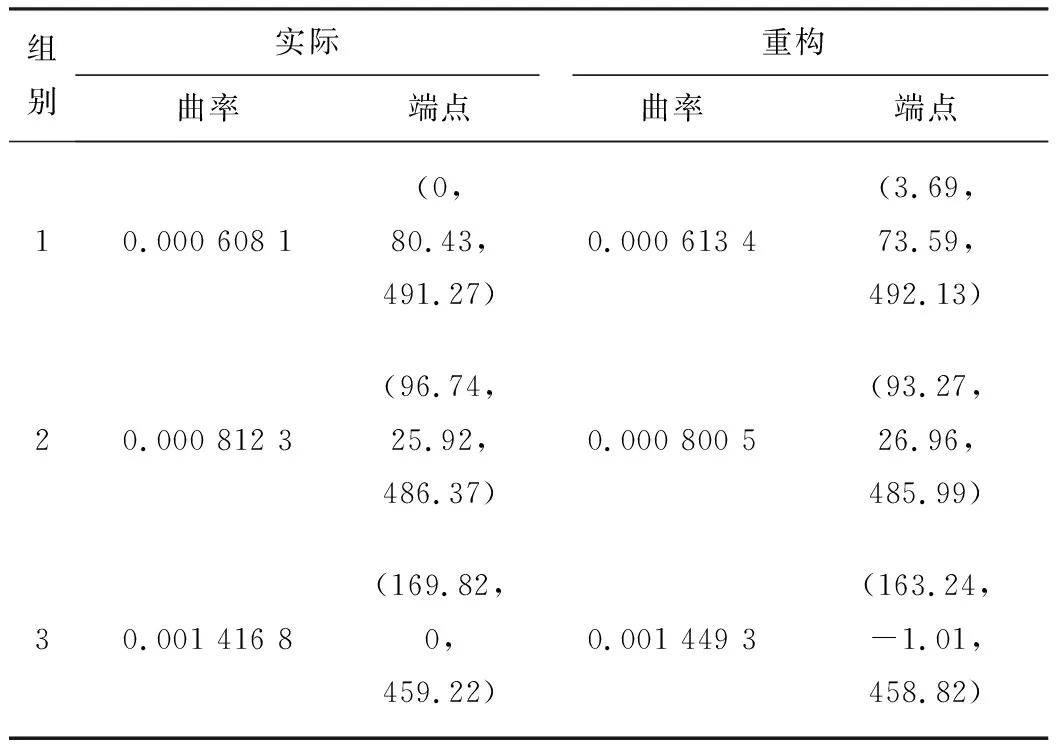
表1 实际与重构结果比较

不同程度弯曲下修正后的曲率结果与实际拟合情况比较吻合，3组曲率相对误差分别为0.87%、1.5%和2.3%，说明形状重构算法反演的曲率信息准确可靠。3组端点位置误差分别为7.8 mm、3.6 mm和6.7 mm，端点位置误差小于1 cm，相对柔体轴向长度的相对误差不超过2%。

结合螺旋倾斜60°升角布置的角度降敏和表面粘贴方式的应变传递，实验中实际应变变化量程达到光纤光栅测量量程的9倍，使原测量范围为6 000 με的石英光纤光栅可以用于测量5.4%的柔体大变形应变检测。

5 结束语

光纤光栅在测量中有良好的重复性和线性度，通过螺旋倾斜的布置方案和表面粘贴方式的应变传递有效地减小了光纤光栅测量应变，扩大了光纤光栅应变检测量程，实现了柔体大变形检测。同时螺旋升角直接影响柔体大变形的应变测量量程，可以根据实际所需最大应变范围选择合适的角度降敏系数，确定螺旋缠绕角度。实验验证光纤检测重构结果与实际变形情况基本一致，该检测方法可以用于柔体大变形的检测与形状重构。