一种MEMS加速度计的噪声处理与参数训练方法

张 旭，路永乐，郭俊启，肖明朗，吴 英

(重庆邮电大学，智能传感技术与微系统重庆市高校工程研究中心，重庆 400065)

0 引言

基于微机电系统(MEMS)的加速度计传感器在尺寸、质量、成本和功耗等方面具有突出的优势，但是由于安装误差、刻度因子、零偏和随机噪声等因素的影响，其输出值存在一定的误差。因此，需要对MEMS加速度计的输出误差进行标定补偿，以提高MEMS加速度计的测量精度。

MEMS加速度计输出误差的标定补偿，主要是对安装误差、刻度因子、零偏等确定性误差的标定和对随机噪声的处理。目前针对确定性误差的标定方法[1-3]，虽然原理和具体方式不同，但是对于MEMS加速度计在不同位置下的实际测量数据，都是取其均值作为该位置的测量值，用于求解或估计所需标定的参数。但是，实际测量数据的均值并不能完全地反映所有的实际测量数据。此外，也没有对实际测量数据中存在的随机噪声进行预处理，噪声误差会遗留在所标定的参数中。而针对随机噪声的处理，H. Wang等[4]利用小波分析算法去噪，杜少林等[5]利用Kalman滤波算法降噪，均没有将噪声处理的结果用于对确定性误差的标定。尹杭等[6]对确定性误差和随机噪声进行了标定和处理，但实际上是独立进行的，在对确定性误差标定之前，没有对实际测量数据中的随机噪声进行预处理。

本文为进一步提高MEMS加速度计的测量精度，以测量值为输入、以真实值为输出建立MEMS加速度计误差补偿模型。利用实验室研制的微惯性测量单元(MEMS-IMU)，采集其加速度计在六位置下3个轴的m组实际测量数据，利用Allan方差和最小均方(LMS)自适应滤波算法对m组实际测量数据进行噪声分析和预处理，处理后的全部数据作为样本用于训练所建模型的参数，利用最小二乘和批量梯度下降相结合的方法获得样本数据对真实模型参数的最优拟合。所建模型在m组样本数据的训练下，能够更加准确地拟合真实模型参数，同时规避了随机噪声对模型参数的污染。实验验证表明，利用该模型对MEMS加速度计进行误差补偿后，输出值的均值误差为(0.72～1.19)×10-4g，标准差为(0.75～1.61)×10-4g，相对于补偿前均值误差降低了2个数量级，标准差降低了1个数量级，有效提高了MEMS加速度计的测量精度和稳定性。

1 MEMS加速度计的误差补偿模型

造成MEMS加速度计输出误差的主要误差项有：安装误差、刻度因子、零偏、随机噪声和二阶非线性误差，由于非线性误差影响较小，忽略非线性误差后的MEMS加速度计实际输出值为

A*=a+(C+K)H+v

(1)

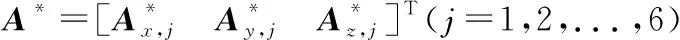
则根据式(1)可得MEMS加速度计的误差补偿模型为

H=S(A-a)

(2)

式中：A=[Ax,jAy,jAz,j]T(j= 1,2,…,6)是经过噪声预处理后的实际测量值矩阵，也是3×m的矩阵。

(3)

Sii(i=x,y,z)是MEMS加速度计3个轴的比例因子，Sij(i,j=x,y,z;i≠j)是各轴之间的非正交因子。

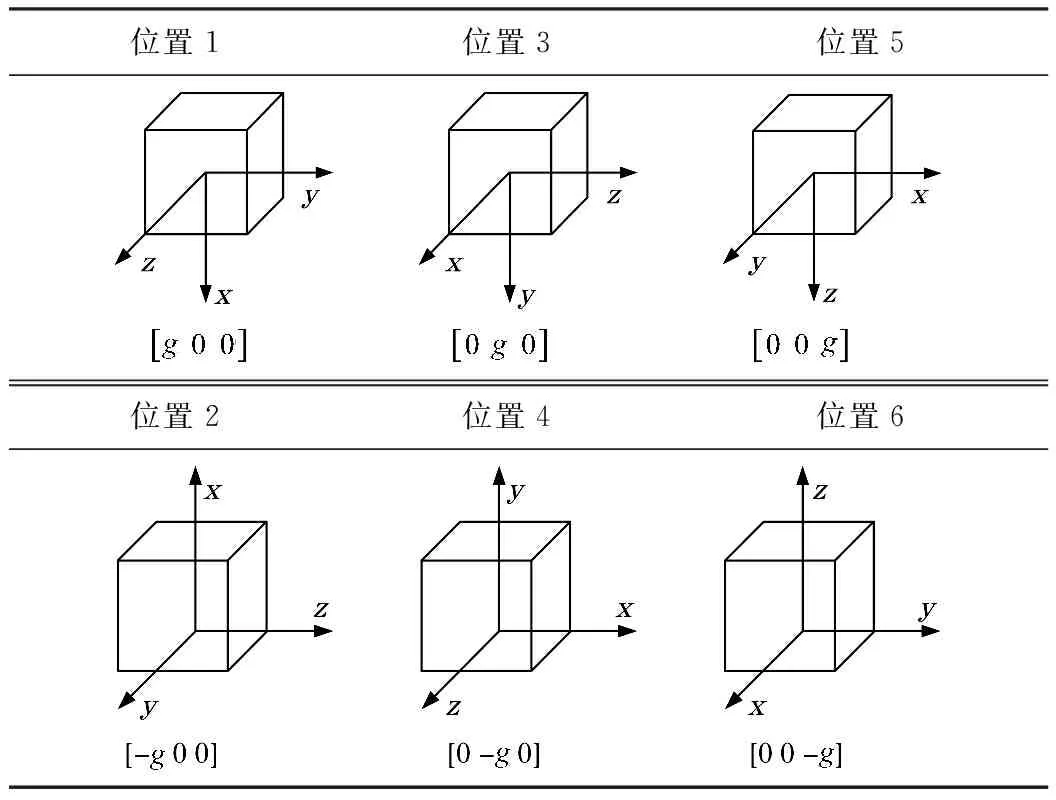
将实验室研制的MEMS-IMU固定在三轴转台上，如图1所示。操作转台依次转动到如表1所示的位置，以50 Hz的采样频率分别采集六个位置下的加速度计3个轴的输出数据，每个位置采集m组数据(m=15 000)。

图1 三轴转台和固定在转台上的MEMS-IMU

表1 6位置坐标轴取向及其重力加速度

位置1位置3位置5位置2位置4位置6

2 随机噪声的预处理

根据之前的分析，所采集到的实际测量数据中含有随机噪声，因此需要对噪声进行预处理后才能作为所建模型的训练样本。本文采用基于LMS自适应滤波算法的噪声抵消器对所采集到的实际测量数据进行处理，抵消器所需的参考噪声参数，则通过Allan方差分析获得。

2.1 LMS自适应滤波算法原理

LMS自适应滤波的原理是利用前一个已经获取的滤波器参数，自动调整当前的滤波器参数，使滤波器的输出与期望参考输入之间的均方误差最小，从而达到最优的滤波效果。LMS自适应滤波算法原理如图2所示。

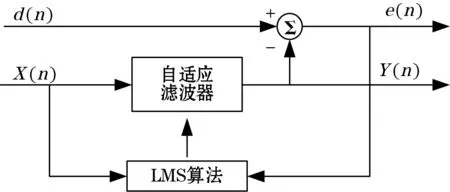
图2 LMS自适应滤波算法原理

图2中，X(n)为滤波器的主输入，Y(n) 为滤波器的输出，d(n) 为滤波器的期望参考输入，e(n) 为滤波器的估计误差输出，n= 1,2,3,…。

滤波器的输出为

Y(n)=WT(n)X(n)

(4)

滤波器的估计误差输出为

e(n)=d(n)-Y(n)

(5)

W(n)为抽头系数向量(权值向量)，其递推更新方程为

W(n+1)=W(n)-μX(n)e(n)

(6)

式中μ为步长因子，控制每次更新后沿着误差函数表面移动的距离，其值满足：0<μ≤ 1/λmax，而λmax是主输入X(n)自相关矩阵的最大特征值。

2.2 LMS自适应滤波噪声抵消器

如果直接使用LMS自适应滤波器对A*进行滤波，很难选取与A相关而与噪声v不相关的期望参考输入d(n)，使最终的滤波输出Y(n)为A。反之，可以利用Allan方差对A*中的噪声v进行分析，进而得到噪声v的模型。然后以噪声v的相关噪声v*为期望参考输入d(n)，以A*为主输入X(n)。利用v与v*的相关性，使滤波输出Y(n)尽量地逼近v*，即相当于估计误差输出e(n)尽量地逼近A。在最优条件下，估计误差输出e(n)即为去除噪声后的A，实现了v与υ*的噪声抵消。如图3所示。

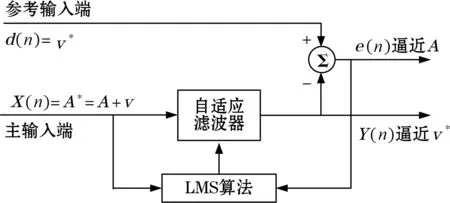
图3 LMS自适应噪声抵消器

2.3 Allan方差分析

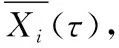
(7)

MEMS加速度计的主要的随机噪声及其Allan标准差、斜率如表2所示[7]。

表2 主要噪声的Allan标准差和斜率

根据式(7)计算加速度计在六位置下3个轴实际测量数据的Allan方差并拟合Allan标准差，以位置1为例，Allan标准差与平均时间的对数图以及所拟合的Allan标准差曲线如图4所示。

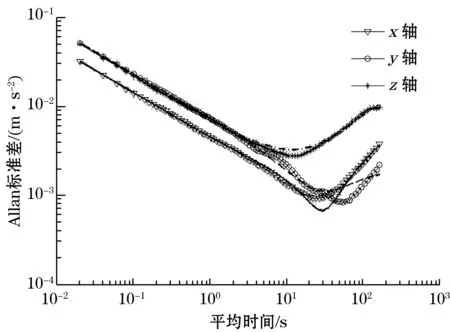
图4 Allan标准差与平均时间关系

由图4中所拟合的Allan标准差曲线的斜率结合表2，可计算MEMS加速度计在位置1处3个轴的各项随机噪声系数，结果如表3所示。

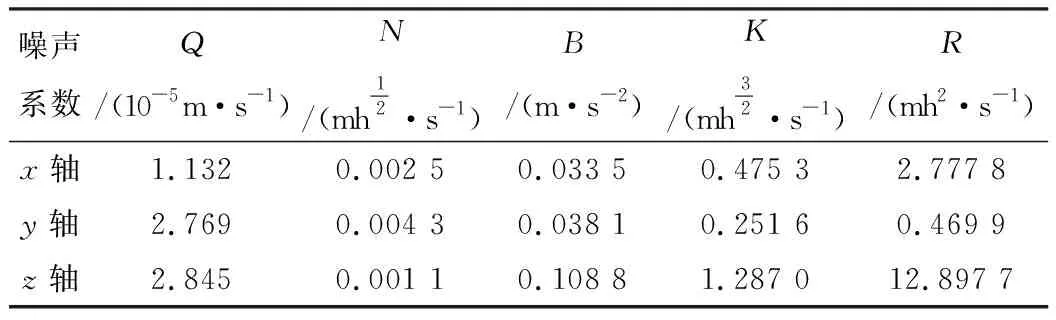
表3 加速度计在位置1下的各项随机噪声系数

上述噪声中，量化噪声Q和速度随机游走N属于白噪声，其余3种噪声属于有色噪声。对于有色噪声，根据有色噪声的功率谱密度函数，由谱分解定理可求解其传递函数，作傅里叶逆变换可得其微分方程如下：

(8)

以互不相关的单位高斯白噪声Ψk(t) (k=1,2,3,4,5)驱动微分方程(8)，可得MEMS加速度计随机噪声的时域模型为

(9)

式中：▽是微分算子；η和ω0为传递函数有理化过程中的调节参数；η取5 Hz，ω0取0.01 rad/s。

2.4 随机噪声预处理结果

以位置1为例，MEMS加速度计3个轴的m组实际测量数据经过LMS自适应滤波噪声抵消器处理前后的对比如图5所示。

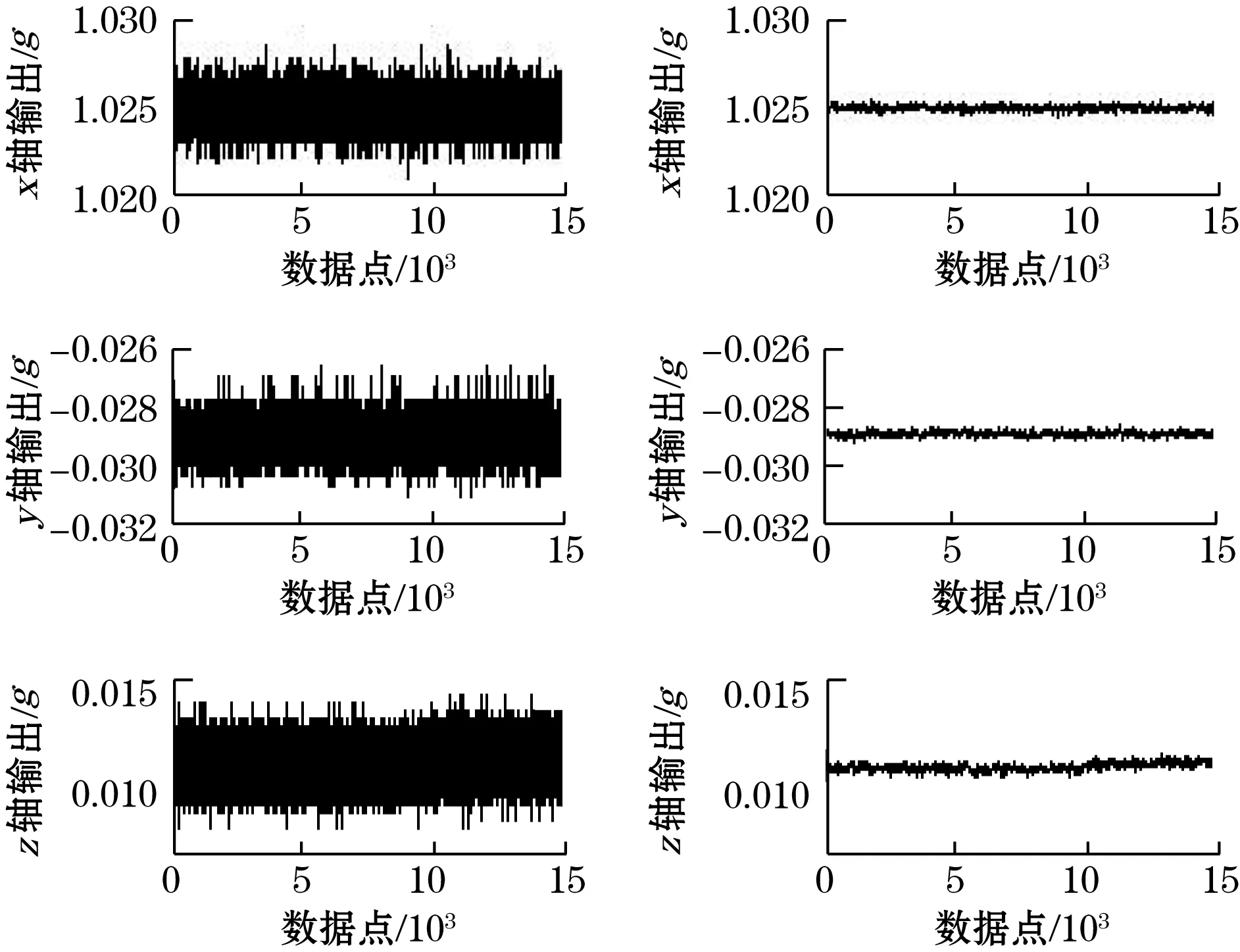
图5 LMS自适应滤波噪声抵消器处理前后对比

3 模型参数训练

所采集的m组实际测量数据经过第2节的预处理后，得到的m组处理后的数据作为样本，用于本节对模型参数的训练。对于所建立的MEMS加速度计误差补偿模型(2)，当加速度计位于位置1和位置2时有：

Hx1=Sxx(Ax1-ax)+Sxy(Ay1-ay)+Sxz(Az1-az)

(10)

Hx2=Sxx(Ax2-ax)+Sxy(Ay2-ay)+Sxz(Az2-az)

(11)

由式(10)与式(11)相减，可得：

(Hx1-Hx2)=Sxx(Ax1-Ax2)+Sxy(Ay1-Ax2)+Sxz(Az1-Az2)

(12)

由式(10)与式(11)相加，可得：

(13)

3.1 最小二乘求解参数矩阵S的先验

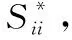
(14)

由最小二乘可得：

(15)

(16)

3.2 批量梯度下降法求解参数矩阵S

将式(12)在未知特征参数λi(i= 1,2,3)下的假设函数写作：

hλ(x)=λ1x1+λ2x2+λ3x3

(17)

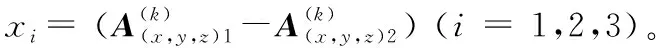
该假设函数的代价函数为

(18)

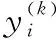
代价函数的梯度为

(19)

特征参数λi的更新方程为

(20)

式中α为学习率，决定沿着能让代价函数下降程度最大的方向移动一次的步长，本文选取的学习率为0.000 3～0.001。

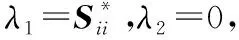
(21)

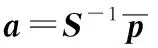
本文整体的算法流程图如图6所示。

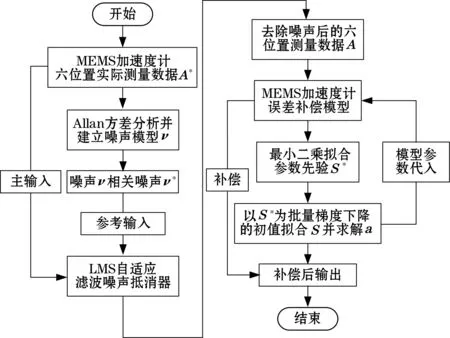
图6 本文算法流程图

4 实验验证与分析

将第3节训练所得模型参数代入误差补偿模型(2)中，以位置1为例，将预处理后的测量数据A(x,y,z)1代入误差补偿模型进行补偿。补偿后的MEMS加速度计3个轴输出值与理论值的对比如图7所示。

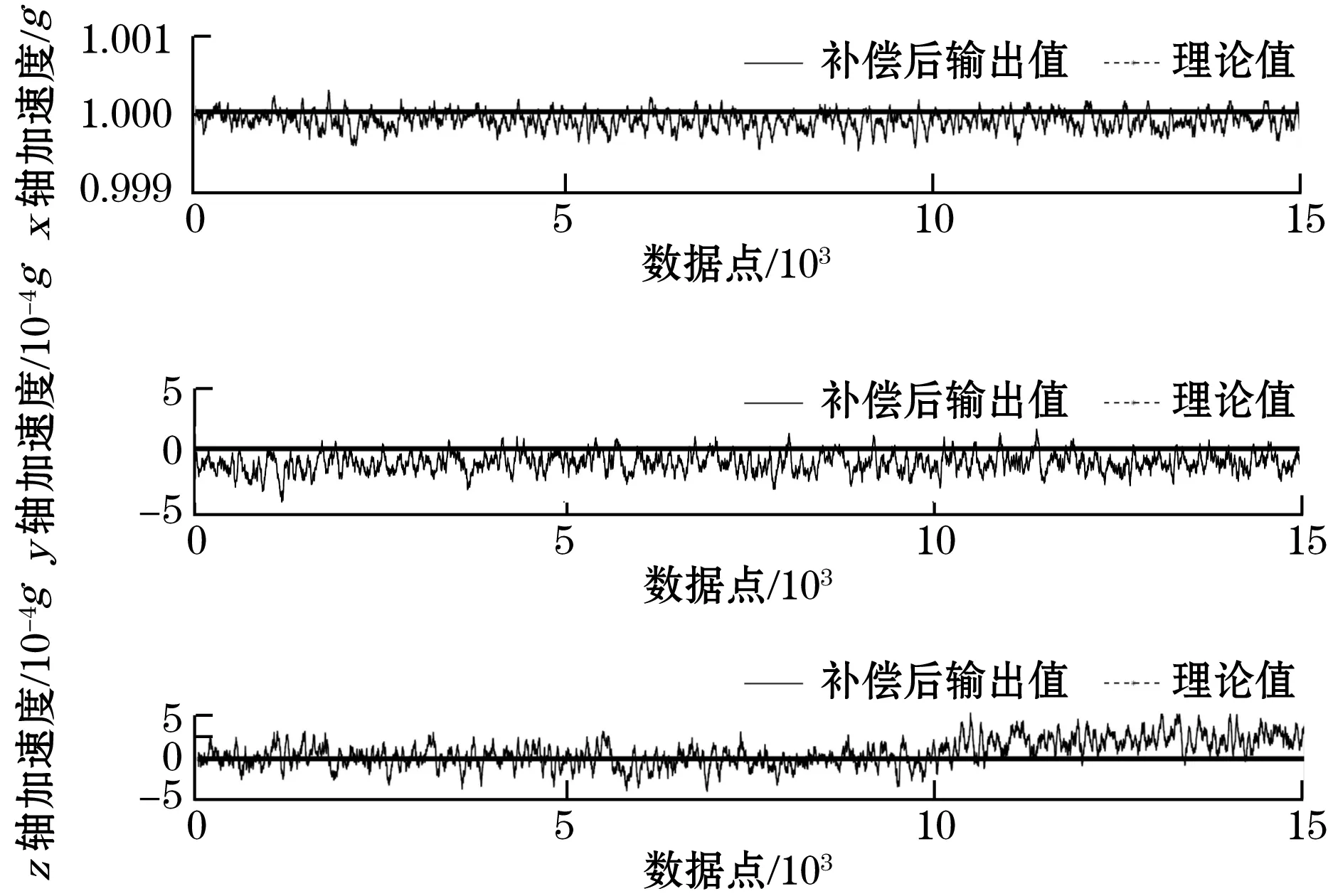
图7 误差补偿后输出值与理论值对比

从图7可以看出，经过误差补偿后，MEMS加速度计3个轴的输出值在理论值附近约10-4g的范围内波动。误差补偿前后加速度计3个轴输出值的均值和标准差如表4所示。

表4 补偿前后三个轴输出值的均值和标准差

从表4中可知，补偿后加速度计三个轴输出值的均值误差为(0.72～1.19) ×10-4g，标准差为(0.75～1.61) ×10-4g，较之补偿前均值误差降低了2个数量级，标准差降低了1个数量级。

5 结束语

本文所提出的MEMS加速度计误差补偿方法，对加速度计在6个位置下的大量实际测量数据进行降噪预处理后，用于训练误差补偿模型的参数，既充分利用了全部的测量数据，也规避了噪声对标定参数的污染，所获得的参数是样本数据对真实参数的最优拟合。经所提方法补偿后，MEMS加速度计输出值的均值误差降低了2个数量级，标准差降低了1个数量级，有效提高了MEMS加速度计的测量精度和稳定性，表明了所提方法的有效性和可行性。