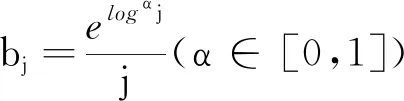NA序列随机和的几乎处处中心极限定理*

井照敬，张 玉

(巢湖学院数学与统计学院，安徽 巢湖 238000)

20世纪80年代，Schatte[1]和Brosamler[2]讨论了几乎处处中心极限定理，近年来，该理论一直是概率极限理论研究的热点.Berkes等[3]构造了一系列独立随机变量序列，使其满足几乎处处中心极限定理但不满足中心极限定理.这说明在实际生活中，几乎处处中心极限定理的应用更广泛.随后，Berkes等[4]推广了文献[3]，在无界函数条件下得到几乎处处中心极限定理.之后，独立随机变量的几乎处处中心极限定理被推广到相依序列[5-7].笔者的主要目的是证明NA序列的随机和序列依然满足几乎处处中心极限定理，且在几种不同权重条件下该结论依然成立.

定义1[1]独立同分布的随机变量部分和的几乎处处中心极限定理的简单形式如下：

其中I(·)为示性函数，Φ(·)为标准正态分布.

定义1是最常见的几乎处处中心极限定理的形式.近年来，该结论通过不同条件在各种相依类型上得到证明.

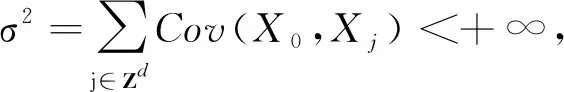
其中Z～N(0,σ2).

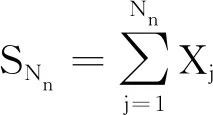
定义2[8]称随机变量X1,…,Xn(n≥1)为负相协的(简记NA), 如果对于任意2个具有相同单调性的函数f1和f2，以及集合{1,2，…，n}的任意2个非空且不相交子集A和B,有

Cov(f1(Xi,i∈A),f2(Xj,j∈B))≤0.

若随机变量X1,X2，…,Xn是NA的,f1,f2,…,fn是非减函数, 则随机变量f1(X1),f2(X2),…,fn(Xn)也是NA的.

定义3[7]称随机变量X1,…,Xn(n≥1)为正相协的(简记PA),如果对于任意2个使得协方差存在且对每个变元均非降的函数g1和g2，以及集合{1,2，…，n}的任意2个非空且不相交子集A和B,有

Cov(g1(Xi,i∈A),g2(Xj,j∈B))≥0.

对于随机变量序列{Xk，k≥1}和{Nn,n≥1}，做出以下假设：

引理2[9]设{Xn,n≥1}是严平稳的、均方可积的相协随机序列，且满足假设(H1)和(H2)，则有

(1)

易证(1)式对于NA序列也成立.

证明记

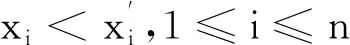
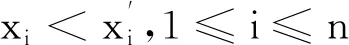
则f-(x1,…,xn)是关于每个分量都非增的函数.关于f+(x1,…,xn)与f-(x1,…,xn)，由单调性可知Cov(f+(x1,…,xn),f-(x1,…,xn))≤0，于是

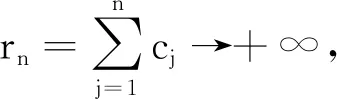
(2)

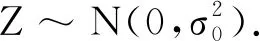
(3)

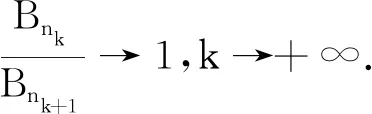
于是由B-C引理可知，

(4)

E(Zn(f))→E(f(Z))n→+∞.

(5)

结合(4)，(5)式，可得

(6)

接下来还需证明

(7)

要证明(7)式成立，可通过如下计算：

其中

(8)

由于|f|是Lipschitz函数，因此由(4)式显然可得

于是

(9)

综上可知(3)式成立.