基于ARMA模型的股票开盘价分析及预测*

陈 浩，兰燕鸿，何郁波

(怀化学院数学与计算科学学院，湖南 怀化 418000)

金融市场存在很多时间序列数据，如不断变动的股价、利率等.不同于截面数据，时间序列数据揭示了系统的运行规律，通过探究其中的规律，可以对未来的走势做出预测，这对投资者来说是十分必要的.目前，购买股票是一种经常性的投资方式，股票市场的波动是国家经济的直接反映，无论是对投资者还是政府来说，股价预测都具有重要意义[1].

传统的股票分析方法有基本分析、演化分析和技术分析等，这些方法只能对股票的走势进行分析和预测，无法预测股票的价格.自回归移动平均(Autoregressive Moving Average，ARMA)模型经过不断的发展，其理论体系非常成熟，在统计分析和数据处理中表现出很好的便利性，且在股票预测过程中不仅考虑了市场指标在时间序列上的相关性，还考虑了随机扰动的干扰性，可以很好地对短期变动趋势做出预测[2].目前，国内学者在时间序列预测方面进行了大量的研究，而ARMA模型作为一类较理想的预测模型，其有效性和适用性自然是研究的重点.有学者选取具有代表性的股指指数或者股票价格作为研究对象，分析其序列值并建立模型，再对未来的趋势进行预测，得到的预测结果与真实值误差较小，进一步证明了ARMA模型在股价预测方面的有效性和适用性[1-4].受这些研究的启发，笔者拟针对具有显著非平稳性的一类时间序列，通过差分方法对原始序列进行平稳化处理，采用最小信息准则确定原始序列所满足的模型，并利用模型对建设银行短期的股票开盘价进行预测，以期为投资者提供合理的投资策略.

1 模型介绍

时间序列是记录系统历史行为的一系列数据，对这些历史数据进行观察、研究，寻找系统的运行规律和结构特征，进而对其未来某一个时刻的行为进行预测，这种分析方法称为时间序列分析[5-7].将具有如下结构的模型称为ARMA模型(简记为ARMA(p,q))：

其中φk(1≤k≤p)和θk(1≤k≤q)为实参数，εt为满足条件的纯随机序列.ARMA模型是平稳时间序列分析中的经典模型，但在经济生活中遇到的时间序列基本上是非平稳序列，因此需要采用一定的方法将其变为平稳序列.一般采用差分的方法对目标序列进行平稳化处理，然后对得到的平稳序列建立ARIMA(p,d,q)模型，其中d为差分阶数.

2 数据获取与预处理

2.1 数据获取

从网易财经选取建设银行(股票代码601939)2018年1月2日至2019年12月26日的每个股票交易日开盘价作为样本数据，将样本记为{PRICE}，共计484个样本数据.表1示出了部分样本数据.

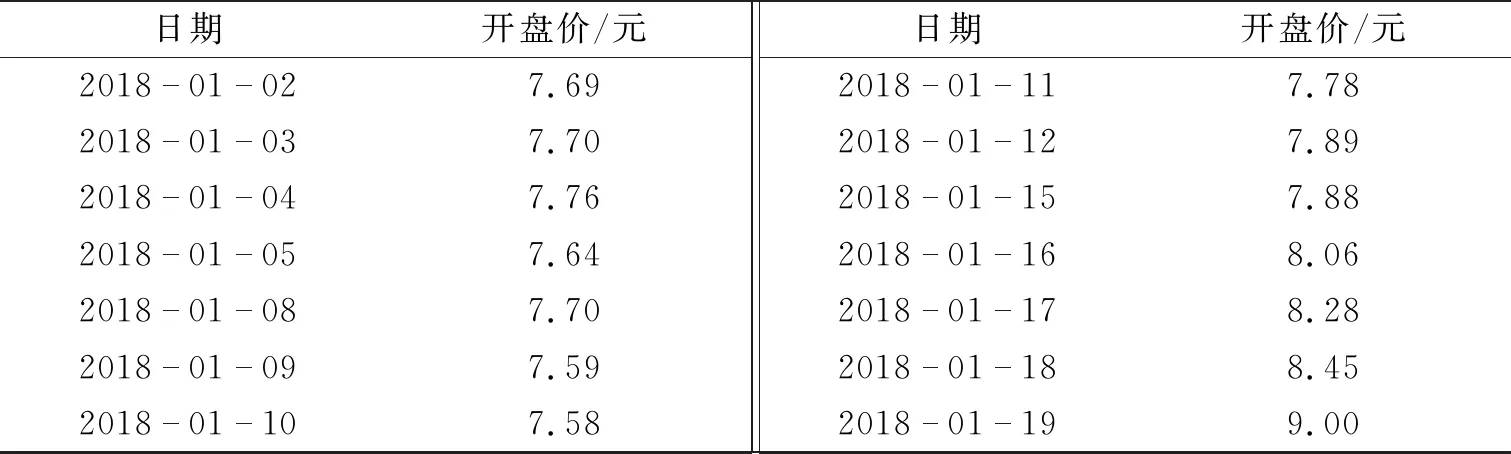
表1 部分样本数据

2.2 数据预处理

首先对序列{PRICE}进行预处理，即平稳性检验和纯随机性检验.若{PRICE}是非平稳序列，则需要采取一定的方法使其平稳化；若{PRICE}是纯随机序列，则表明它的序列值之间没有任何联系，换言之，该序列没有任何研究价值.

(1)平稳性检验.由于股市受到许多不确定性因素的影响，市场波动较大，因此股票价格序列一般为非平稳时间序列.对原始序列的平稳性检验，可以采用原始序列的时序图和自相关图相结合的方法来进行识别.利用EViews软件[8]绘出序列{PRICE}的时序图，如图1所示.从图1可以看出，{PRICE}具有明显的趋势性，从而初步判断{PRICE}是非平稳序列.一个具有长期趋势的非平稳序列，它的一个显著特征是随着延迟期数的增加，自相关系数会缓慢衰减至0.从图2所示的滞后24期的序列自相关图可以看出，自相关系数一直在零轴的右边，其值都位于2倍标准差外并呈现缓慢减小的趋势.由此可知，选取的建设银行股票价格序列是一个非平稳时间序列.

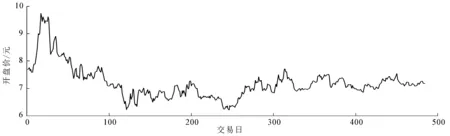
图1 序列{PRICE}的时序图

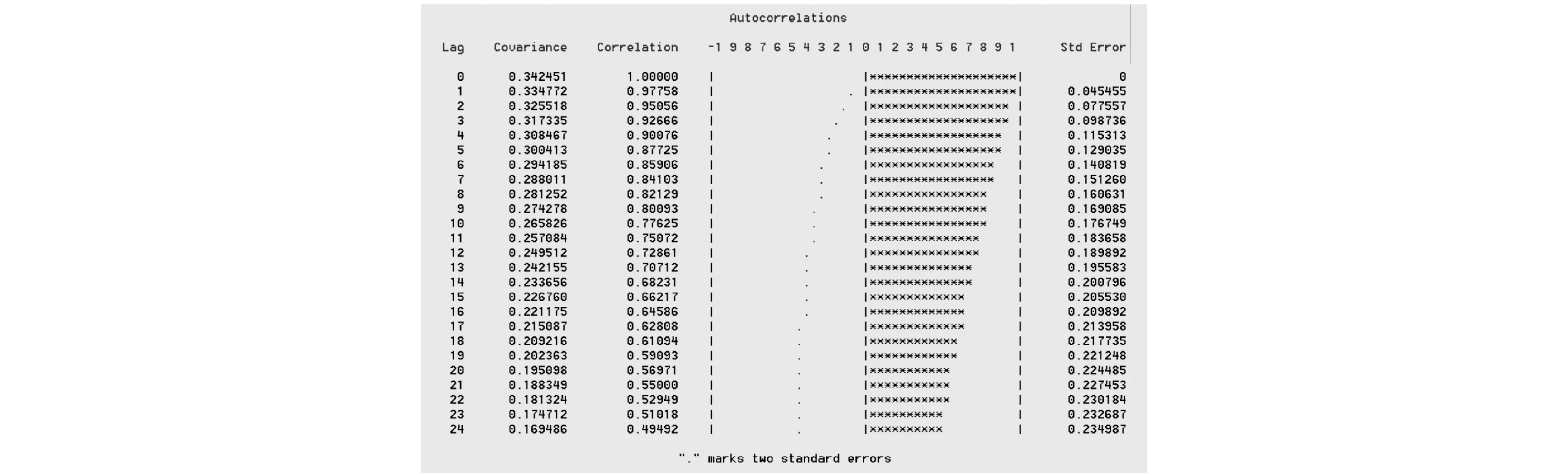
图2 {PRICE}序列自相关图

(2)数据平稳化处理.差分运算是平稳化处理常用的方法，对序列{PRICE}做一阶差分运算，得到新的序列为{D(PRICE)}，且满足D(PRICE)t=PRICEt-PRICEt-1.绘出序列{D(PRICE)}的时序图，如图3所示.

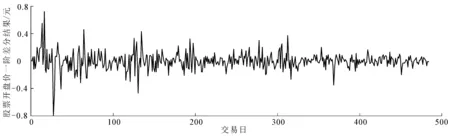
图3 一阶差分{D(PRICE)}时序图

从图3可以看出，序列{PRICE}通过一阶差分运算之后不再具有趋势性.差分后序列值始终在0值上下振动，且振幅有界，从而初步判断序列{D(PRICE)}是平稳的.为了验证初步判断的正确性，对序列{D(PRICE)}进行平稳性ADF检验.若序列拒绝原假设，则说明此序列平稳.ADF检验结果见表2，从表2可知，1%显著水平下的临界值为-3.443 691，ADF的t统计量的值为-19.711 47.显然，1%的显著水平下的临界值要远大于ADF检验值，说明在99%的置信水平下拒绝原假设，即该序列不存在单位根，所以序列{D(PRICE)}是平稳的.

表2 一阶差分序列ADF检验结果

(3)纯随机性检验.利用EViews软件对序列{D(PRICE)}进行纯随机性检验，结果见表3.从表3可知，滞后6，12，18期的P值都明显小于0.05，说明残差序列的Q值全都大于检验水平为0.05的χ2分布临界值，所以{D(PRICE)}不是纯随机序列，具有相关性.

表3 白噪声检验结果

3 模型的建立

3.1 模型识别

序列{PRICE}通过差分运算之后变为平稳时间序列{D(PRICE)}，现可以通过{D(PRICE)}的自相关系数和偏自相关系数的衰减方式确定模型的类型.由一阶差分后序列的自相关图(图4)和偏自相关图(图5)可以看出，序列{D(PRICE)}仅有不超过5%的样本的自相关系数和偏自相关系数落在2倍标准差之外，因此AFC和PAFC都可视为拖尾.根据ARMA模型的识别原则，可以尝试使用ARMA模型进行拟合.

图4 {D(PRICE)}序列自相关图

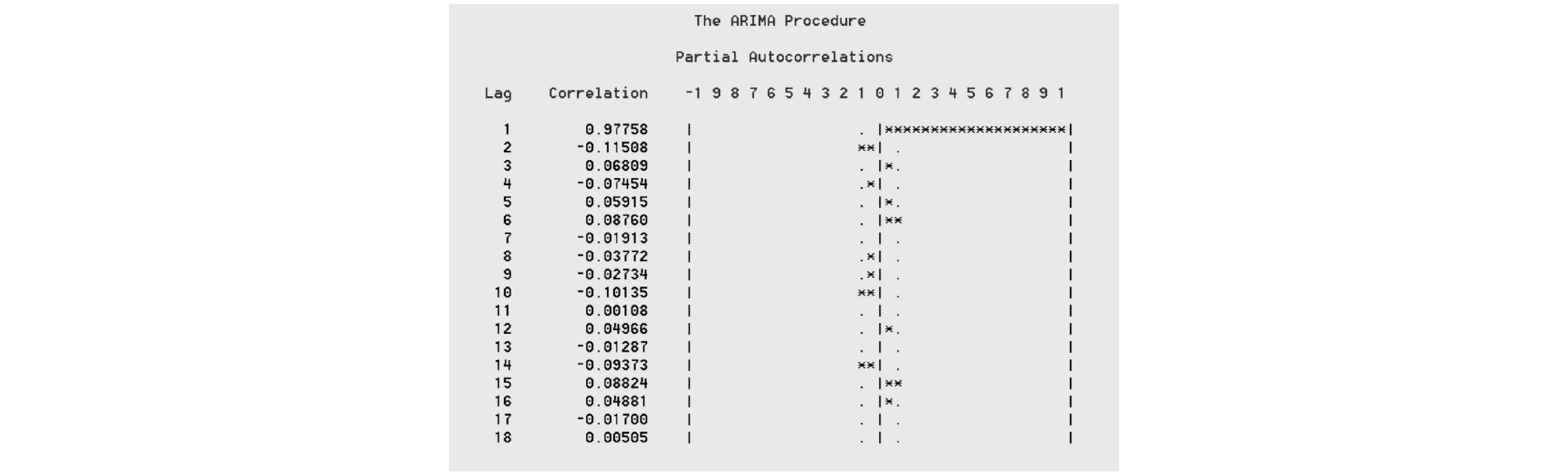
图5 {D(PRICE)}序列偏自相关图

3.2 模型定阶

确定对序列{D(PRICE)}采用ARMA模型拟合之后，还需要确定ARMA模型滞后项p和q的值.根据图4建立所有p，q≤5的ARMA模型，利用AIC，SB，HQ准则和t统计量显著性来具体确定模型的阶数.由于数据较多，表4仅给出包含信息准则最小的模型在内的部分模型数据，从中可知ARIMA(5,1,4)模型的AIC和HQ的值最小，所以选择ARIMA(5,1,4)建立模型.

表4 部分ARIMA模型的AIC，SC，HQ检验值

表4(续)

对ARIMA(5,1,4)模型进行估计，确定AR(5)项(即D(PRICE)t-5)和常数项的系数不显著，因此需要剔除AR(5)项和常数项.继续利用最小AIC准则和SBC准则进行拟合估计，识别出最优模型为ARIMA(4,1,4).通过检验，ARIMA(4,1,4)模型的所有系数都十分显著，于是采用该模型对序列{D(PRICE)}进行拟合.

3.3 参数估计

最小二乘估计法计算模型的参数值具有较高的精度，因此采用最小二乘法对ARIMA(4,1,4)模型的参数进行估计，即估计方程组

中的参数φ1,φ2,φ3,φ4,θ1,θ2,θ3,θ4，得到ARIMA(4,1,4)模型的口径为

其中εt为残差序列.模型的特征根都在单位圆内，故平稳可逆.

3.4 模型的检验

模型建立后，需要检验模型的有效性.一个最优的拟合模型应将样本中的全部相关信息提取完毕，因此对模型的残差序列进行纯随机性检验.若残差序列不是纯随机序列，即残差序列中还包含未被充分提取的信息，则需要对模型进行优化；若残差序列纯随机，即拟合残差项中不含有可以被提取的有效信息，则模型显著有效.利用EViews软件对残差进行检验，ARIMA(4,1,4)模型的残差序列无任何趋势，为一平稳序列.Q统计量检验的结果显示，所有的P值都大于0.05，说明拟合模型的残差序列是一个纯随机序列，因此该模型是显著有效的.

4 模型的应用

股票市场受多方面因素的影响，其价格浮动较大.随着时间的延长，这些不确定因素对模型预测效果产生的影响会进行叠加，因此长期预测的误差一般较大，而短期预测的效果较好.采用ARIMA(4,1,4)模型预测建设银行2019-12-27，2019-12-30，2019-12-31这3个交易日的股票开盘价，结果见表5.

表5 建设银行股票开盘价短期预测结果

从表5可知，开盘价的预测值与实际值之间的相对误差均小于1.5%，说明ARIMA(4,1,4)模型对于短期预测具有较高的吻合度，股票日的开盘价预测95%的置信区间很好地包含了实际值.利用ARIMA(4,1,4)模型对484个交易日的开盘价进行预测，结果如图6所示，图中虚线所夹部分为置信水平95%的置信区间，中间实线表示预测值.

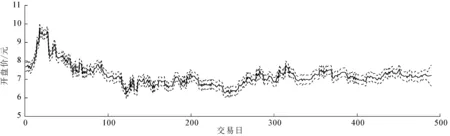
图6 建设银行股票开盘价预测的95%置信区间结果

5 结语

通过EViews软件结合ARMA模型对建设银行的股票开盘价序列进行分析，得到符合股价的模型口径.采用ARIMA(4,1,4)模型进行预测，结果显示，该模型对建设银行股票开盘价的短期预测效果较好，且拟合模型充分提取了建设银行股票开盘价序列中包含的有用信息.当然，本研究存在一定的局限性，如在对原始序列和差分后序列的分析过程中带有一定的主观性和经验性，尤其是对序列的自相关函数及偏自相关函数的分析；另外，在序列分析的过程中，应该考虑国家宏观经济政策等其他因素对序列的影响，因此可以参考选用序列的条件异方差模型.