基于去噪自编码器的镜像极限学习机设计*

龙求青，廖柏林，印煜民

(吉首大学信息科学与工程学院，湖南 吉首 416000)

极限学习机(Extreme Learning Machine, ELM)是单隐含层前馈神经网络中一种全新的学习算法，因其具有训练速度快、泛化性能优等特点[1]，被广泛应用于疾病诊断[4]、交通标志识别[5]和图像评价[6]等领域.与传统的训练算法(如BP算法[2])不同，ELM的输入权值和隐含层偏置是随机产生的，且在训练过程中保持不变，输出权值则是由利用最小化平方损失函数求解Moore-Penrose广义逆运算而得到的最小范数最小二乘解所确定的[3].这整个过程中不用迭代，只需设定隐含层的神经元个数和激活函数.近年来，深度学习技术在提取高维数据特征方面表现卓越，有学者将此优点引入到ELM中，以提升ELM处理高维数据的性能[7-9].但在实际应用中，因ELM的输入权值是随机产生的，故随着数据样本维度的增加，为了保证分类性能，ELM需要大量的隐含层节点作为支撑[10].大量隐含层节点的使用会增大网络结构的复杂度，降低网络模型的效率，对ELM进入深度学习领域及处理高维度大数据样本产生一定的阻碍.所以，如何在不明显降低ELM分类性能的前提下缩减隐含层节点数，简化网络结构，成为当前亟待解决的难题.

ELM和类似于ELM的神经网络都是随机生成输入权值和分析输出权值的[11-22].为了优化ELM的隐含层节点数，笔者尝试用伪逆法确定输入权值，随机生成输出权值.由于这种权值确定方式与ELM的权值设定方式互为镜像，因此称新算法为镜像极限学习机(Mirror Extreme Learning Machine，MELM).因深度学习技术能够提取到样本数据更抽象的特征，笔者拟将去噪自编码器(Denoising Autoencoder, DAE)与MELM组合成新的神经网络学习算法，即基于去噪自编码器的镜像极限学习机(DAE-MELM)，以期提升镜像极限学习机的分类性能和抗噪性.

1 极限学习机与去噪自编码器

1.1 极限学习机

设有N个任意不同的样本集(xi,yi),其中xi=(xi1,xi2,…,xin)T∈Rn为输入向量(样本的特征)，yi=(yi1,yi2,…,yim)T∈Rm为对应的样本标签向量.在输入神经元个数为N、隐含层神经元个数为L和输出神经元个数为m且激活函数为f(·)的ELM网络中，整个神经网络的矩阵表达式为

Hβ=Y.

(1)

其中：β=(β1,β2,…,βL)T，为权值矩阵，位于隐含层和输出层之间；Y=(y1,y2,…,yN)T，为训练样本期望输出矩阵；

1.2 镜像极限学习机

MELM与ELM的结构相似，也由输入层、隐含层和输出层构成.假设MELM有J个输入层、K个输出层和M个隐含层神经元，激活函数为非线性函数f(·).称第m(m=1,2,…,M)个隐含层神经元与第k(k=1,2,…,K)个输出层神经元的连接权值为输出权值，用umk表示，其值在区间[a1,a2]中随机产生；称第j(j=1,2,…,J)个输入层神经元与第m个隐含层神经元的连接权值为输入权值，用wjm表示，其值由伪逆法确定.第m个隐含层神经元的偏置bm，其值在区间[a3,a4]中随机产生.于是，第k个输出层神经元的输出

(2)

其中pj为第j个输入层神经元的输入.(2)式的矩阵表达式为

Q=Uf(WP-B).

(3)

其中：Q=(q1,q2,…,qK)T∈RK×1；P=(p1,p2,…,pJ)T∈RJ×1；B=(b1,b2,…,bM)T∈RM×1；U和W分别是输出权值矩阵和输入权值矩阵，

定理1假设激活函数f(·)是严格单调的，输出权值U和偏置B分别选自区间[a1,a2]和[a3,a4]，则最优的输入权值W=(f-1(U+Q)+B)P+，其中f-1(·)表示f(·)唯一的逆函数.

证明(3)式两边同时左乘U+，得到

U+Q=U+Uf(WP-B)=f(WP-B).

(4)

求解(4)式的反函数，得到f-1(U+Q)=WP-B，即

WP=f-1(U+Q)+B.

(5)

(5)式两边同时右乘P+，得到WPP+=(f-1(U+Q)+B)P+，即W=(f-1(U+Q)+B)P+.证毕.

1.3 去噪自编码器

DAE是在自编码器的基础上改进而来的一种算法.与自编码器不同之处是，DAE在原始的输入数据中加入了噪声，要求神经网络在此条件下重构出原始的输入数据，并力求误差最小.这样就迫使DAE主动去摆脱噪声的干扰，提取出输入数据更深层次的特征.DAE由编码器和解码器2个部分组成，位于输入层和隐含层之间的为编码器，位于隐含层和输出层之间的为解码器.DAE的网络结构如图1所示.

图1 DAE的网络结构

DAE的训练过程如下:

2 基于去噪自编码器的镜像极限学习机

MELM可以实现快速分类，且仅需少量的隐含层神经元个数，但样本的数据维度和噪声对其分类性能影响较大.鉴于DAE能在高维数据中找出那些受噪声影响较小的核心特征，因此将DAE与MELM相结合，由DAE负责生成MELM的输入数据，MELM负责对数据进行模式分类，这样不仅可以提升分类器处理高维含噪声数据的能力，而且可以降低网络的复杂度，加快分类速度.DAE-MELM的网络结构如图2所示.

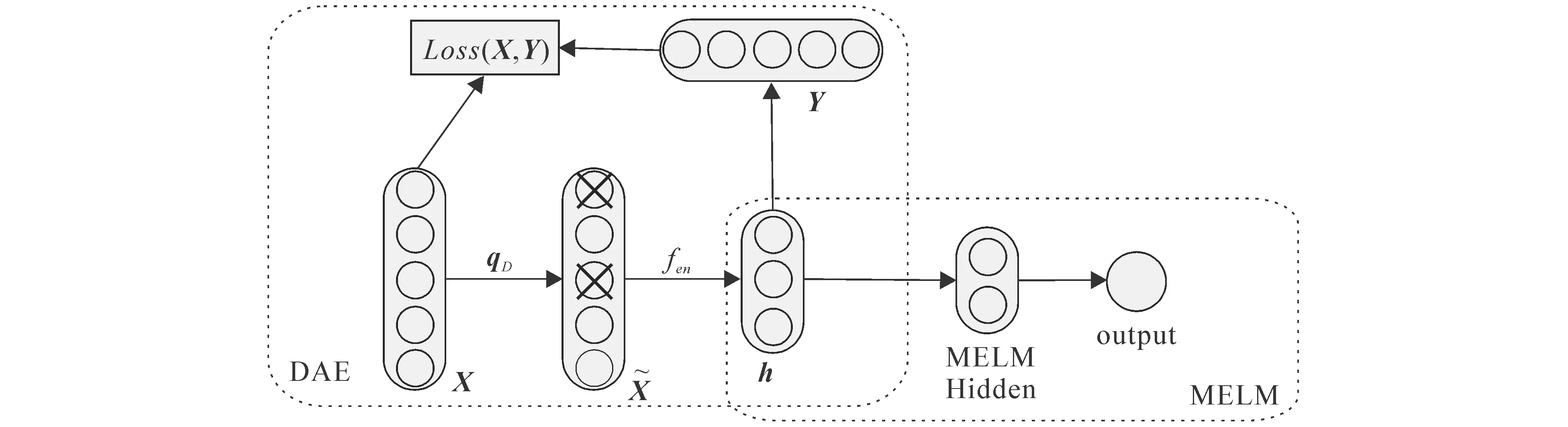
图2 DAE-MELM的网络结构

DAE-MELM的训练过程如下:

(ⅰ)训练DAE网络.网络训练结束后，提取出最终得到的隐含层输出向量.

(ⅱ)将DAE的隐含层输出向量作为输入数据，用MELM对其进行分类，从而完成整个网络的训练.网络的最终输出即为分类结果.

3 实验部分

3.1 实验环境

实验平台为 Intel i5-4200U 1.6 GHz，4 GB内存的PC，实验在64位的Windows7系统上用Matlab2012(b)软件实现.

3.2 实验数据

选取4个公开的高维数据集，即MNIST，Fashion MNIST，Rectangles和Convex.对每个数据集分别加入10%的高斯白噪声和10%的椒盐噪声，形成含有噪声的新数据集.表1给出了4个公开数据集的详细说明.

表1 4个公开数据集的说明

3.3 实验结果

3.3.1 DAE-MELM网络结构的确定 在神经网络训练过程中，输入层神经元个数依赖于训练数据的维数，输出层神经元个数依赖于训练数据的类别数，因此在已明确训练数据的情况下确定神经网络的结构，仅需确定神经网络隐含层节点数.笔者将采用试错法，即按照预先设定的范围标准不断调整隐含层节点数，同时记录网络性能最优时的隐含层节点数，从而得到最优网络结构.

首先，选取原始的Fashion MNIST数据集对MELM进行训练，观察在训练集和测试集中隐含层节点数对分类错误率的影响趋势(图3)，节点数的取值范围为[10,50].

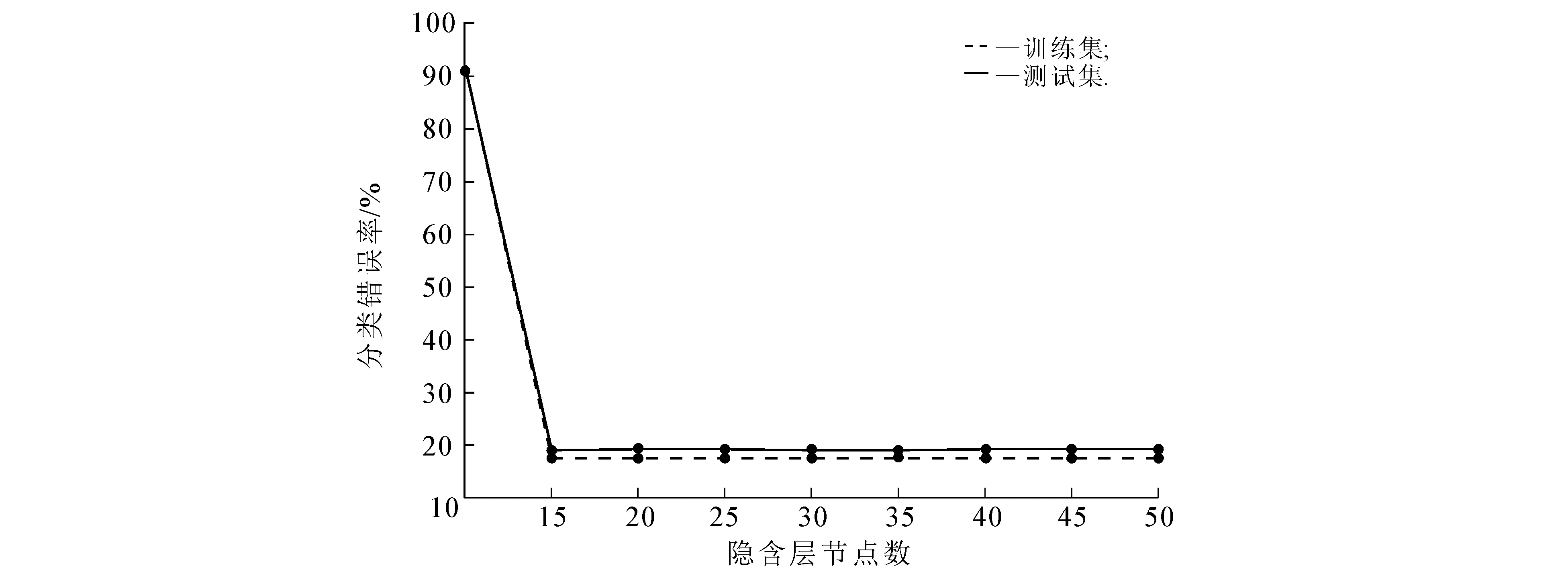
图3 MELM隐含层节点数对分类错误率的影响

由图3可以看出：隐含层节点数在[10,15)范围内递增时，分类错误率快速下降；节点数在[15,20]范围内递增时，分类错误率的下降趋势放缓；节点数大于20时，分类错误率的下降趋势平稳且错误率较低.因此，设定MELM的隐含层节点数为20.

然后，通过重复实验的方法确定DAE隐含层的节点数.DAE-MELM的分类错误率随隐含层节点数的变化趋势如图4所示.

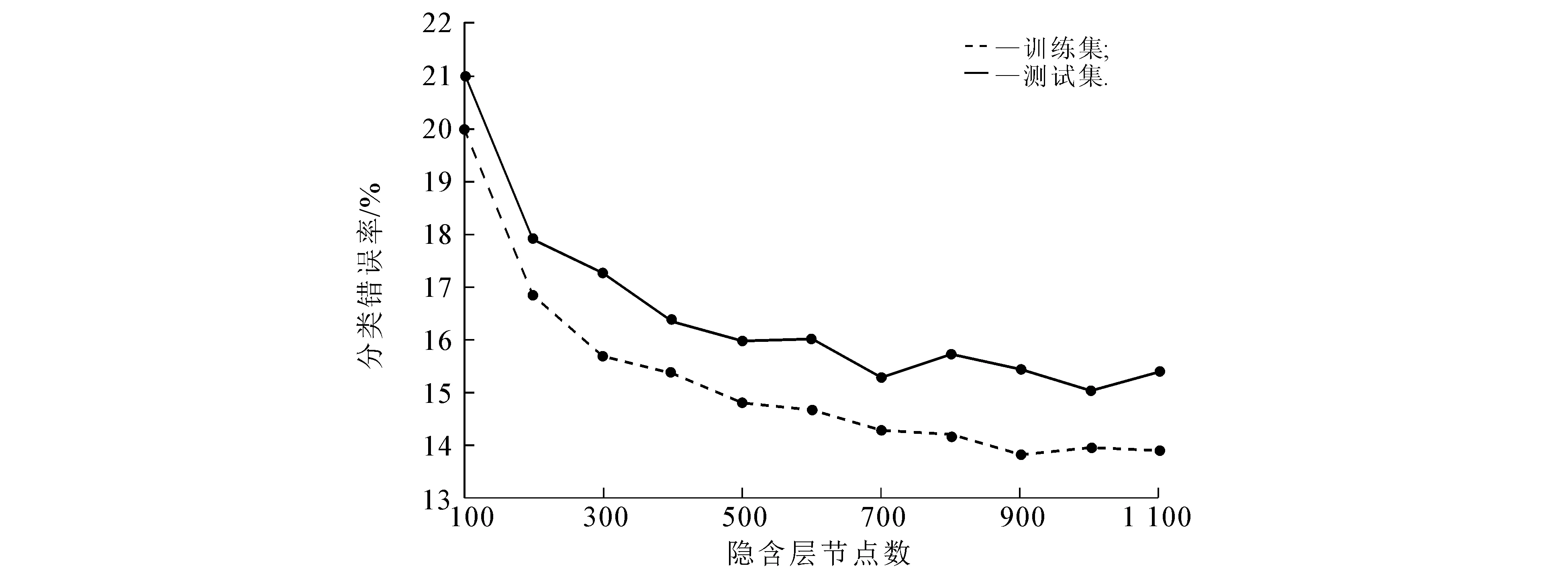
图4 DAE-MELM隐含层节点数对分类错误率的影响

由图4可以看出：随着隐含层节点数的增加，分类错误率逐步下降；当节点数大于700时，分类错误率较低且在一个小范围内波动.考虑到时间与空间的复杂度，在保证分类错误率较低的同时还要保证网络的紧凑性，所以设定DAE的隐含层节点数为700.

综上确定DAE-MELM的最佳网络结构为780-700-20-S，其中780为数据集的样本输入，S为类别数(即样本对应的输出).

3.3.2 不同算法分类错误率对比分析 在MNIST，Fashion MNIST，Rectangles和Convex数据集及其加入10%高斯白噪声和10%椒盐噪声后的数据集中，将DAE-MELM与ELM，PCA-ELM(Principal Components Analysis-ELM)，SAA-2(2 Hidden Layer Stacking Autoencoders)和DAE-ELM进行分类性能比较.其中，ELM的网络结构为784-1 500-S，PCA-ELM的网络结构为784-1 500-S，SAA-2的网络结构为784-200-200-S，DAE-ELM的网络结构为784-200-1 500-S，各算法结构均为重复实验后性能最佳的结构[9].ELM，PCA-ELM，SAA-2与DAE-ELM在各数据集中的实验结果来自于文献[9].5种算法的分类错误率见表2.

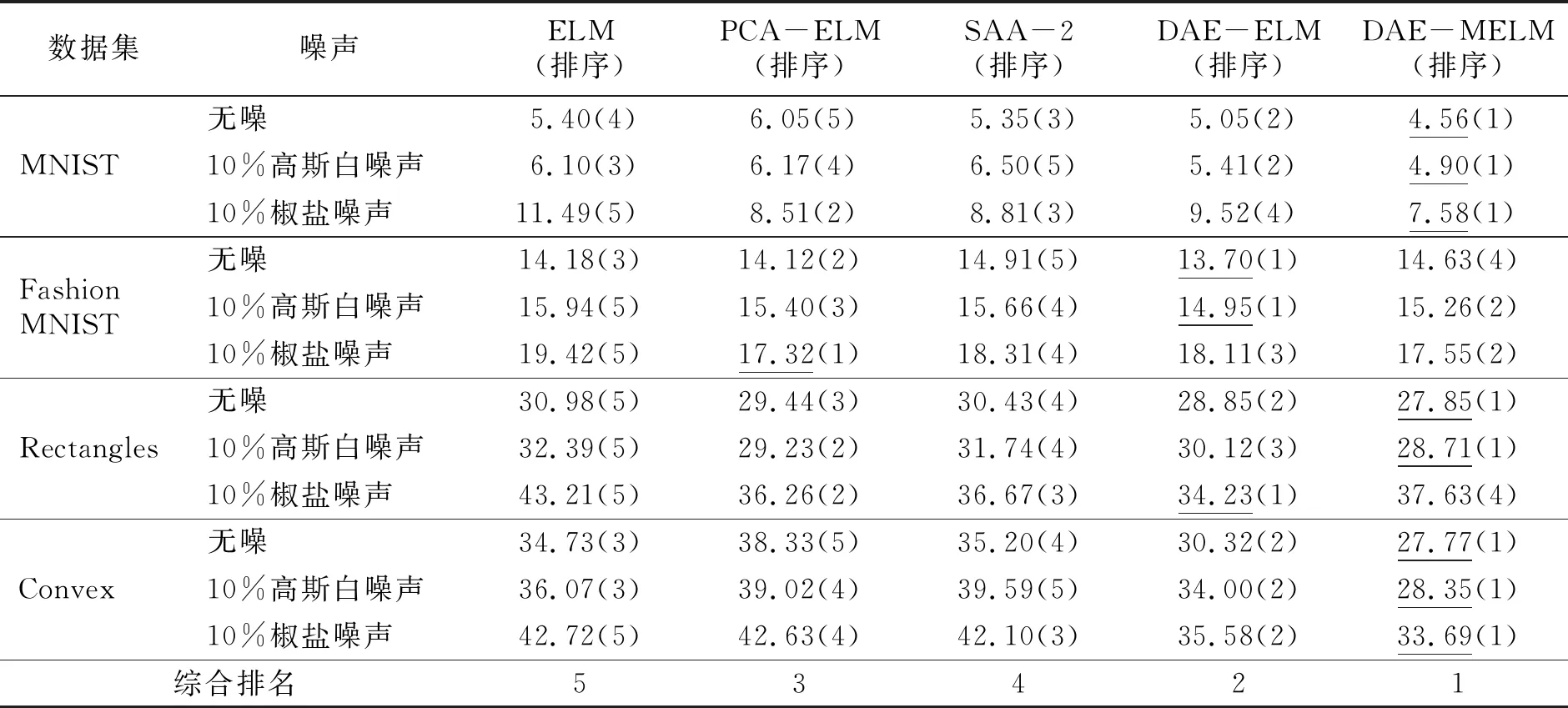
表2 ELM，PCA-ELM，SAA-2，DAE-ELM和DAE-MELM的分类错误率

由表2可知，无论数据集是否含有噪声，相比于ELM，PCA-ELM，SAA-2和DAE-ELM，DAE-MELM在绝大多数数据集上都可以显著降低网络分类错误率.对各算法的实验结果进行综合排名，结果显示，DAE-MELM的综合分类性能最佳，且用于模式分类的隐含层节点数最少.

4 结语

为了解决ELM处理高维度、含噪声数据需要大量隐含层节点以保证其分类性能的问题，笔者采用伪逆法确定输入权值，随机生成输出权值，设计出MELM.为了提升MELM的抗噪性和鲁棒性，将MELM与DAE相结合，由DAE生成MELM的输入数据，MELM对数据进行模式分类.实验结果表明，无论数据集中是否含有噪声，DAE-MELM相比于ELM，PCA-ELM，SAA-2和DAE-ELM，分类错误率下降的同时还极大地缩减了隐含层节点数，分类性能得以整体提高.这为ELM在深度学习领域中的应用提供了新的思路.