变动区间上的确界函数是连续函数的证明*

邢家省，吴 桑，杨义川

(1.北京航空航天大学数学科学学院，北京100191；2.数学、信息与行为教育部重点实验室，北京100191)

闭区间上的连续函数在变动区间上的上确界函数和下确界函数是连续函数，这个结果在文献[1-2]中有完整的论证，其方法是利用确界函数的单调性来证明确界函数的左连续和右连续，从而证明确界函数是连续的.由于该证明过程较长，叙述麻烦，不利于掌握和传播，因此笔者拟在文献[3-9]的基础上，给出连续函数在变动区间上的确界函数是一致连续的简单证明.

1 2函数的上确界相减的不等式

定理1[3-4]设f(x),g(x)在I上有定义且有界，则有：

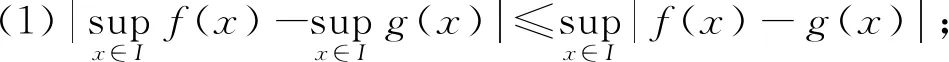
证明(1)由

f(x)=(f(x)-g(x))+g(x)≤|f(x)-g(x)|+g(x)≤

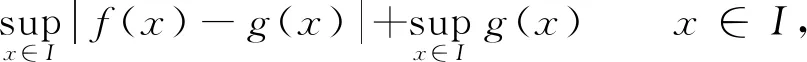
(2)由

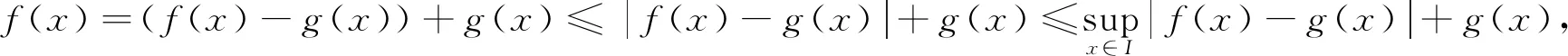
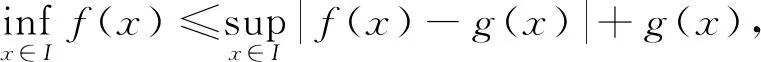
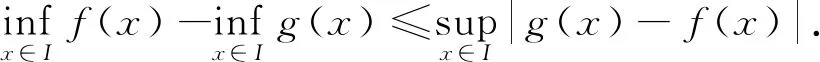
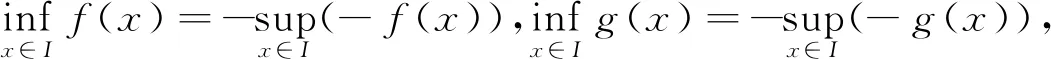
(3)利用(1)可得，

(4)利用(2)可得，

定理1在研究一致收敛的函数列的性质方面起着重要作用[5-9].

2 连续函数在变动区间上的确界函数的一致连续性

由f(x)在[a,b]上连续可知f(x)在[a,b]上一致连续.对于∀ε>0，存在δ>0，当x1,x2∈[a,b]，|x1-x2|<δ时，有|f(x1)-f(x2)|<ε，于是当x,x0∈[a,b]，|x-x0|<δ时，

|((1-u)a+ux)-((1-u)a+ux0)|≤|x-x0|<δu∈[0,1]，

|f((1-u)a+ux)-f((1-u)a+ux0)|<ε，

从而|M(x)-M(x0)|<ε,即M(x)在[a,b]上连续.

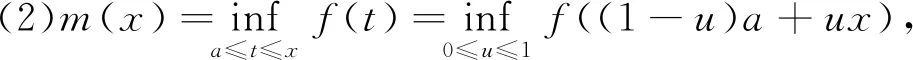
由f(x)在[a,b]上连续可知f(x)在[a,b]上一致连续.对于∀ε>0，存在δ>0，当x1,x2∈[a,b]，|x1-x2|<δ时，有|f(x1)-f(x2)|<ε，于是当x,x0∈[a,b]，|x-x0|<δ时，

|((1-u)a+ux)-((1-u)a+ux0)|≤|x-x0|<δu∈[0,1]，

|f((1-u)a+ux)-f((1-u)a+ux0)|<ε，

从而|m(x)-m(x0)|<ε,即m(x)在[a,b]上连续.

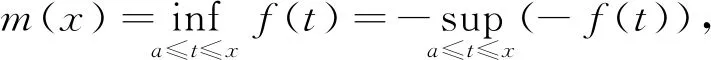
从定理2的证明过程可以发现，其实是直接证明M(x)和m(x)在[a,b]上一致连续.由定理2的证明可得如下结果：

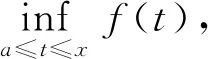
3 二元函数在变动区间上的确界函数的一致连续性

定理5设f(x,y)在[a,b]×[c,d]上连续，对于∀x∈[a,b]，y∈[c,d]，记

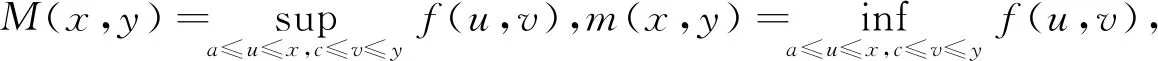
则M(x,y)和m(x,y)在[a,b]×[c,d]上一致连续.

证明记xt1=(1-t1)a+t1x，yt2=(1-t2)c+t2y，则有

由f(x,y)在[a,b]×[c,d]上连续，可得f(x,y)在[a,b]×[c,d]上一致连续.对于∀ε>0，存在δ>0，当x1,x2∈[a,b]，y1,y2∈[c,d]，|x1-x2|<δ，|y1-y2|<δ时，有|f(x1,y1)-f(x2,y2)|<ε，于是

即M(x,y)在[a,b]×[c,d]上一致连续.

由

可得m(x,y)在[a,b]×[c,d]上一致连续.

二元确界函数的连续性是一个新发现的问题，文献[1-2]中的方法不适用.这里将变动区间上的确界函数转化为固定区间上的确界函数，即将问题一般化，就比较容易解决了.

由定理5的证明可得如下结果：

定理6设f(x,y)在[a,b)×[c,d)上连续，对于∀x∈[a,b)，y∈[c,d)，记

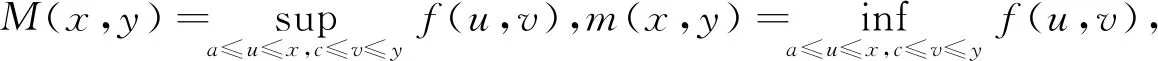
则M(x,y)和m(x,y)在[a,b)×[c,d)上连续.

定理7设f(x,y)在[a,+∞)×[c,+∞)上一致连续，对于∀x∈[a,+∞)，y∈[c,+∞)，记

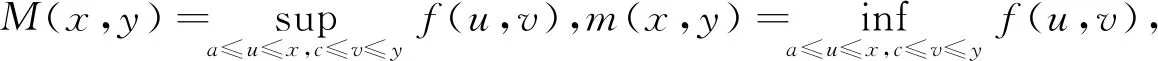
则M(x,y)和m(x,y)在[a,+∞)×[c,+∞)上一致连续.

4 2函数的上确界相减的不等式的应用举例

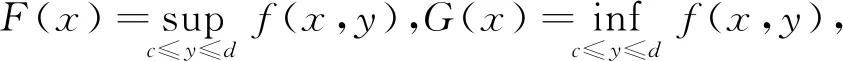
证明由f(x,y)在[a,b]×[c,d]上连续，可得f(x,y)在[a,b]×[c,d]上一致连续.对于∀ε>0，存在δ>0，当x1,x2∈[a,b]，y1,y2∈[c,d]，|x1-x2|<δ，|y1-y2|<δ时，有|f(x1,y1)-f(x2,y2)|<ε，于是

即F(x)在[a,b]上一致连续.同理可证G(x)在[a,b]上一致连续.

由定理8的证明可得如下结果：

定理9设f(x,y,z)在[a,b]×[c,d]×[e,f]上连续，对于∀x∈[a,b]，记

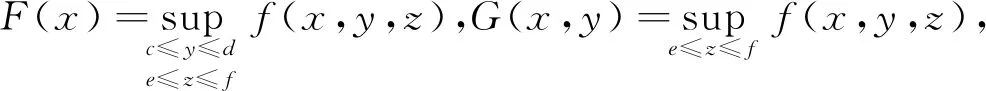
则F(x)在[a,b]上连续，G(x,y)在[a,b]×[c,d]上一致连续.