在给定区间上求含参一元二次不等式的解集问题

袁福蓉

【摘要】求解一元二次不等式的解集，关键在于画出其相对应的函数图像，结合图像就可得到对应不等式的解集.对于求含参一元二次不等式的解集也是如此.本文着重对含有参数的一元二次不等式的解法作了详细分析，主要分为常数项含参、一次项含参、二次项含参，并对每种类型题的解法作了归纳总结.从中我们可以看到通过数形结合，可以指导学生明确分类的标准，学会解题.通过对含参一元二次不等式的求解，可以提高学生数形结合与分类讨论的核心素养.

【关键词】一元二次不等式;含参数;分类讨论;数形结合

数形结合与分类讨论是高中很重要的两个核心素养.求解含参一元二次不等式的解集，关键在于画出其相对应的函数图像.而二次函数是函数中的一个非常重要的模型，贯穿整个高中的学习.解不等式，求最值，利用导数求函数的单调区间等都会有它的身影，所以，刚进入高中学习的同学们学好二次函数极其重要.含参二次函数的学习是同学们学会数形结合与分类讨论数学核心素养的一个重要方式.

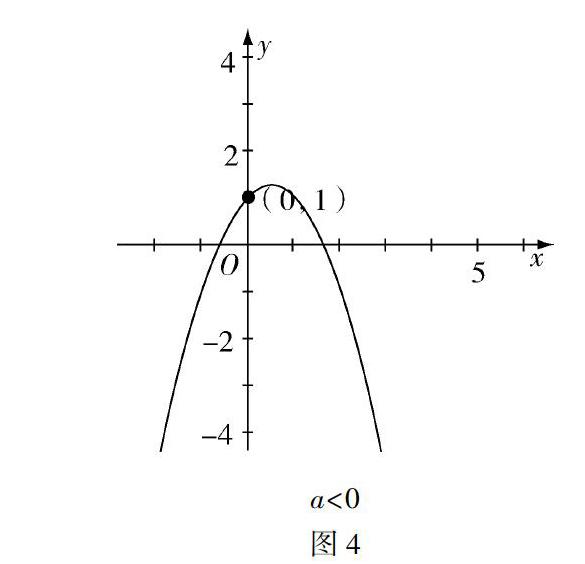
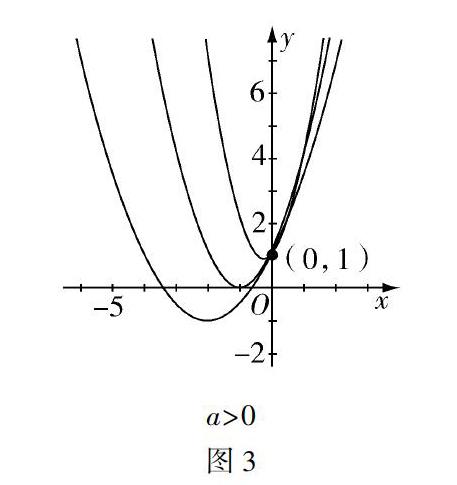
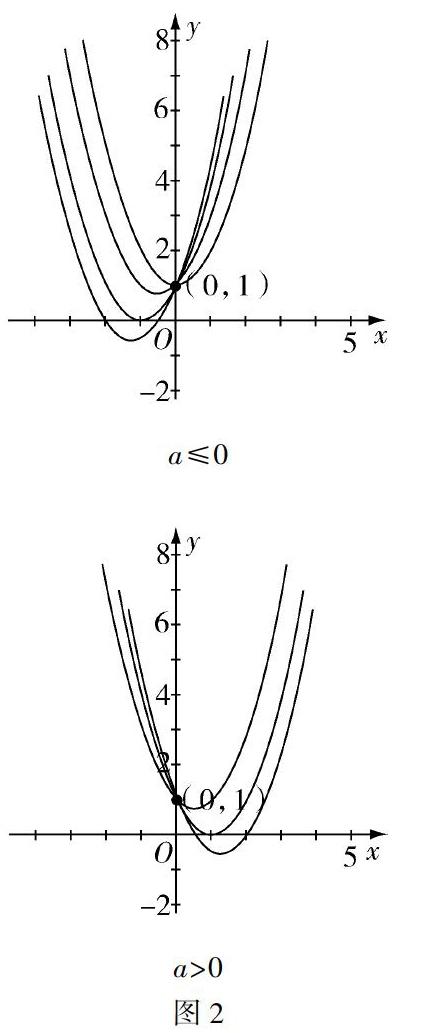
在初中，同学们都已经学习过了二次函数，知道它的关键在于图像开口方向，对称轴，与x轴的交点个数（根據判别式Δ的正负情况判断）以及特殊点处的函数值等.但是一旦二次函数的系数里面含有参数，那么又该如何去讨论呢？如何作出其二次函数的图像呢？下面对参数所在位置做以下归纳，以期能对同学们形成分类讨论的意识以及学会数形结合的思想有所帮助.

一、常数项含参数