游隙对滚滑轴承内部载荷及应力影响的研究*

□ 魏延刚 □ 徐荣浩 □ 刘彦奎

大连交通大学 机械工程学院 辽宁大连 116028

1 研究背景

田红平等提出国内首个关于滚滑复合轴承的专利,且通过有限元分析和现场试验,证明了在牙轮钻头较高转速工况下,滚滑复合轴承依然有很高的承载能力和很长的使用寿命[1]。虽然田红平等证明了牙轮钻头采用滚滑复合轴承的优点,但是其它滚滑复合轴承专利产品的实际应用目前尚未见报道。若基于高承载能力的特点,将滚滑轴承应用于风力发电机齿轮箱,从而延长风力发电机齿轮箱轴承的使用寿命,这无疑具有重要的实用价值。

相比常规滚动轴承和滑动轴承,滚滑轴承这一新型轴承的研究仍较少。韩传军等[2]用空心滚子替换滚滑轴承的实心滚子,通过有限元分析验证替换后的滚滑轴承具有较好的应力分布,同时对滚子空心度进行了优化分析。卢黎明、秦豫江等[3-5]提出一种螺旋弹性滚子,进行了实心圆柱滚子、空心圆柱滚子、螺旋弹性滚子在应力分布和动态特性等方面的对比分析,得出螺旋弹性滚子优于其它两种滚子的结论。卢黎明、曾国文等[6]应用有限元方法对滚滑轴承的动力学问题进行仿真分析,得到滚滑轴承各零件最大应力的分布及动态变化规律,但研究结论有待商榷。卢黎明、曾国文[7]还应用有限元方法,通过结构热应力耦合对滚滑轴承滑块与内外圈滚道接触面的温度场进行了分析。曾国文[8]对滚滑轴承的力学特性及疲劳寿命进行了分析。梁大伟[9]应用有限元软件分析了滚滑轴承的静力学、动力学和温度场,并研究了滚子与滑块的协调性。

轴承内部载荷分布是研究轴承力学特性、使用寿命和可靠性等的基础,然而,关于滚滑轴承内部载荷分布的论文尚未见发表。虽然常规滚动轴承理论内部载荷计算方法无法应用于滚滑轴承,但是根据滚动轴承基本原理和接触力学基本原理,应用有限元方法可以求得滚滑轴承内部载荷分布。

由接触力学[10]可知,滚子与套圈滚道是非贴合性接触,滑块与套圈滚道是贴合性接触,因此,滚子与套圈滚道的接触面积很小,滑块与套圈滚道的接触面积则大很多。在相同位置角时,滚滑轴承滑块受到的应力远小于滚子所受到的应力,而滑块承受的载荷则远大于滚子承受的载荷。前期许多学者对滚滑轴承内部载荷分布进行研究，也证明了这一点。滚滑轴承在工作时,滑块受到的摩擦力远大于滚子受到的摩擦力,会对滚滑轴承的启动速度产生影响。同时，摩擦力做功产生较大的摩擦损耗,会影响滚滑轴承的工作温升和使用寿命。对此，有必要减小滑块与套圈滚道之间的摩擦损耗，改善滚滑轴承的启动性能。笔者设计了滑块和套圈滚道之间有一定游隙的滚滑轴承,应用有限元方法对不同游隙的滚滑轴承进行仿真,以研究游隙对滚滑轴承内部载荷及应力分布的影响,为滚滑轴承的基础理论研究和参数优化,以及应用于风力发电机齿轮箱提供参考。

2 有限元模型

根据2 MW风力发电机齿轮箱轴承实际使用场合,参照圆柱滚子轴承国家标准,取滚滑轴承的滚子及滑块数各为17个,确定滚滑轴承的基本参数如下：轴承内径为170 mm，轴承外径为310 mm，内圈滚道直径为208 mm，外圈滚道直径为272 mm，滚子直径为32 mm，滚子长度为52 mm，滑块长度为52 mm。滑块结构如图1所示。

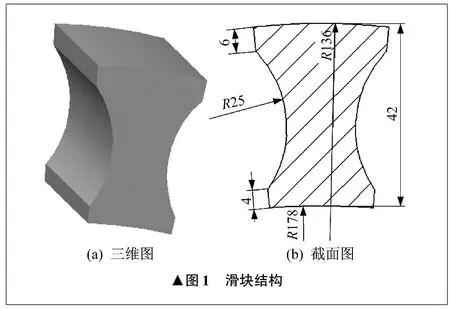
▲图1 滑块结构

根据滚动轴承基本原理，建立滚滑轴承有限元分析模型，合理简化对内部载荷分布和应力分布无影响或影响甚微的局部细节。同时，为了提高计算效率,利用轴承结构和载荷的对称性,取滚滑轴承的1/4建立有限元模型。为方便描述,将滚子和滑块按照逆时针方向进行编号。为充分研究滚滑轴承的承载性能,取滚滑轴承轻载、中载和重载三个不同大小的径向载荷工况,对滚滑轴承的两个典型工作位置进行分析，工位1为滚子在最下端,工位2为滑块在最下端，如图2所示。2 MW风力发电机齿轮箱中速轴上使用的Nj2234圆柱滚子轴承，其基本额定动载荷为1 040 kN,分别取1/4基本额定动载荷的5%、10%、20%，作为滚滑轴承轻载13 kN、中载26 kN、重载52 kN三种工况进行分析。

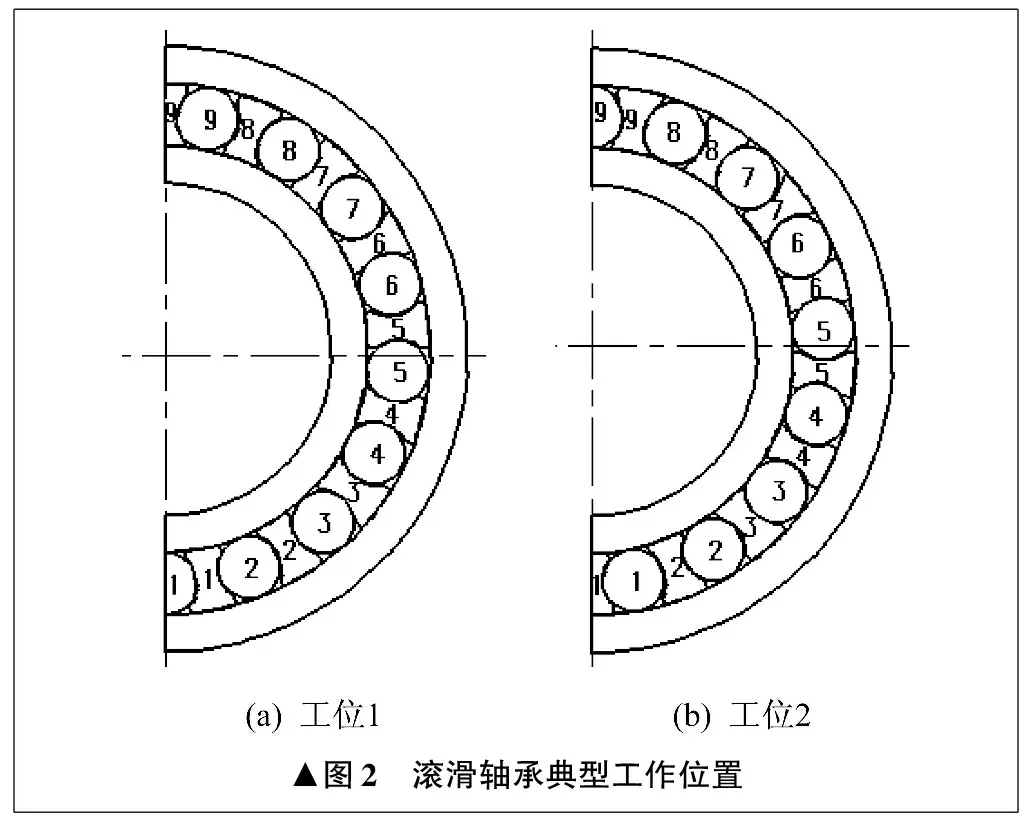
▲图2 滚滑轴承典型工作位置

圆柱滚子及滑块的材料均选用GCr15轴承钢,弹性模量为219 GPa,泊松比为0.3,密度为7.83 g/cm3。内圈、外圈的材料选用G20CrNi2MoA轴承钢,弾性模量为205 GPa,泊松比为0.29,密度为7.88 g/cm3。为了在保证计算精度的同时尽量减少计算时间,对发生接触及容易出现边缘效应的区域进行网格细化。滚滑轴承有限元网格模型如图3所示。

▲图3 滚滑轴承有限元网格模型

2 MW风力发电机齿轮箱中速轴上使用的轴承在实际工作时为外圈固定、内圈旋转,施加的边界条件为外圈外表面约束所有自由度,滚滑轴承1/2轴截面上内圈、外圈、滚子和滑块的截面约束轴向移动自由度,滚滑轴承1/2径向截面上内圈、外圈、滚子和滑块的截面约束垂直于截面方向的移动自由度，径向载荷施加在内圈孔表面。分别建立圆柱滚子与内圈滚道、圆柱滚子与外圈滚道、滑块与内圈滚道、滑块与外圈滚道的接触对,采用面对面接触方式,且接触静摩擦因数均设为0.1。仿真分析时设置三个分析步，分别对内圈径向施加轻载、中载和重载。

3 结果分析

基于不同载荷、两个典型工作位置,应用有限元方法对不同游隙滚滑轴承进行仿真分析,重点研究游隙对滚滑轴承内部载荷及应力分布的影响。

以零游隙时为例,对滚滑轴承各主要元件受载后的应力分布进行介绍。在径向轻载、中载、重载作用下,滚滑轴承的滚子、滑块在两个典型工作位置分别与轴承内、外圈滚道接触时所受到的等效应力高应力区分布规律相似,但等效应力的大小不同,最大等效应力出现的位置也有所不同。另外,滚滑轴承的接触应力分布规律与等效应力基本一致,只是最大接触应力的数值大于最大等效应力。重载作用下工位1滚滑轴承的等效应力云图如图4所示。由图4可见,最大等效应力出现在1号滚子与内圈的接触边缘,滚滑轴承的高应力区分布在1号～5号滚子和1号～4号滑块上,且从1号滚子到5号滚子应力逐渐减小,从1号滑块到4号滑块应力逐渐减小。由1号滚子和1号滑块的等效应力云图可以清晰看出，滚子和滑块的边缘效应引起边界应力集中，1号滚子等效应力最大值为821.7 MPa，1号滑块等效应力最大值为287.8 MPa。

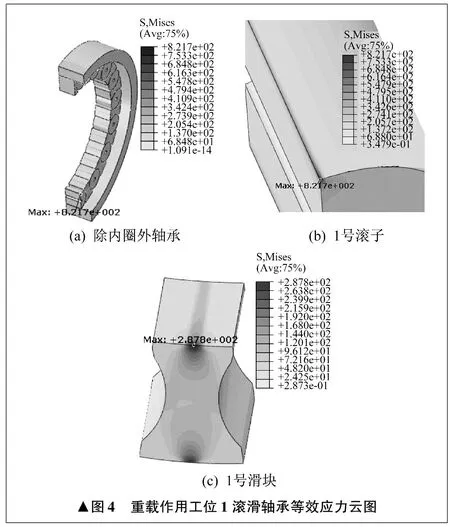
▲图4 重载作用工位1滚滑轴承等效应力云图

研究不同大小游隙对滚滑轴承内部载荷及应力分布的影响。工位1时1号滚子及1号滑块在零游隙与0.1 mm游隙时内部载荷与最大等效应力变化曲线分别如图5、图6所示。图中横坐标分析步中，第一个分析步由零载荷线性加载至轻载13 kN，第二个分析步由轻载13 kN线性加载至中载26 kN，第三个分析步由中载26 kN线性加载至重载52 kN。

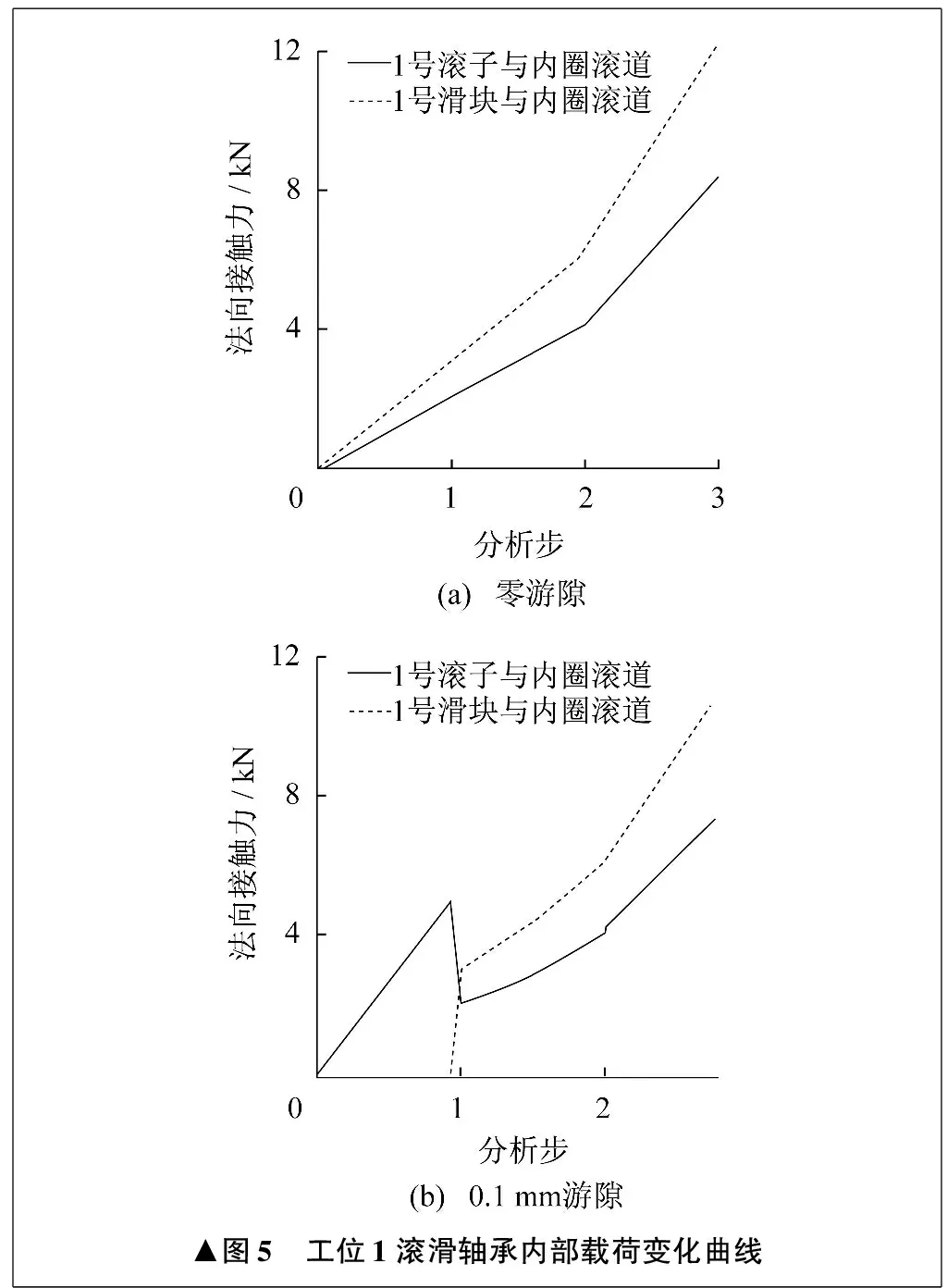
▲图5 工位1滚滑轴承内部载荷变化曲线

由图5可见,零游隙时,随着外部载荷的增大,1号滚子和1号滑块受到的法向接触力都增大,且1号滑块受到的法向接触力一直大于1号滚子。0.1 mm游隙时,在轻载区间内,随着外部载荷的增大,1号滚子受到的法向接触力逐渐增大,1号滑块不承受法向接触力。到一定外部载荷时,1号滚子受到的法向接触力突然减小,而1号滑块开始受到法向接触力，此时可定义外部载荷为滑块受载的临界载荷,即使滚滑轴承中滑块承受载荷的最小外部径向载荷。之后,随着外部载荷的增大,1号滑块受到的法向接触力大于1号滚子。

由图6可见,零游隙时,1号滚子受到的最大等效应力随着外部载荷的增大而增大,且始终大于1号滑块。0.1 mm游隙时,在轻载区间内,随着外部载荷的增大,1号滚子的最大等效应力逐渐增大,1号滑块不承受等效应力。随着外部载荷增大至临界载荷,1号滚子的最大等效应力突然减小,1号滑块开始承受等效应力,但承受的最大等效应力始终小于1号滚子。

其它受载滚子及滑块的载荷与应力分布规律与1号滚子及1号滑块一致，只是数值大小不同。

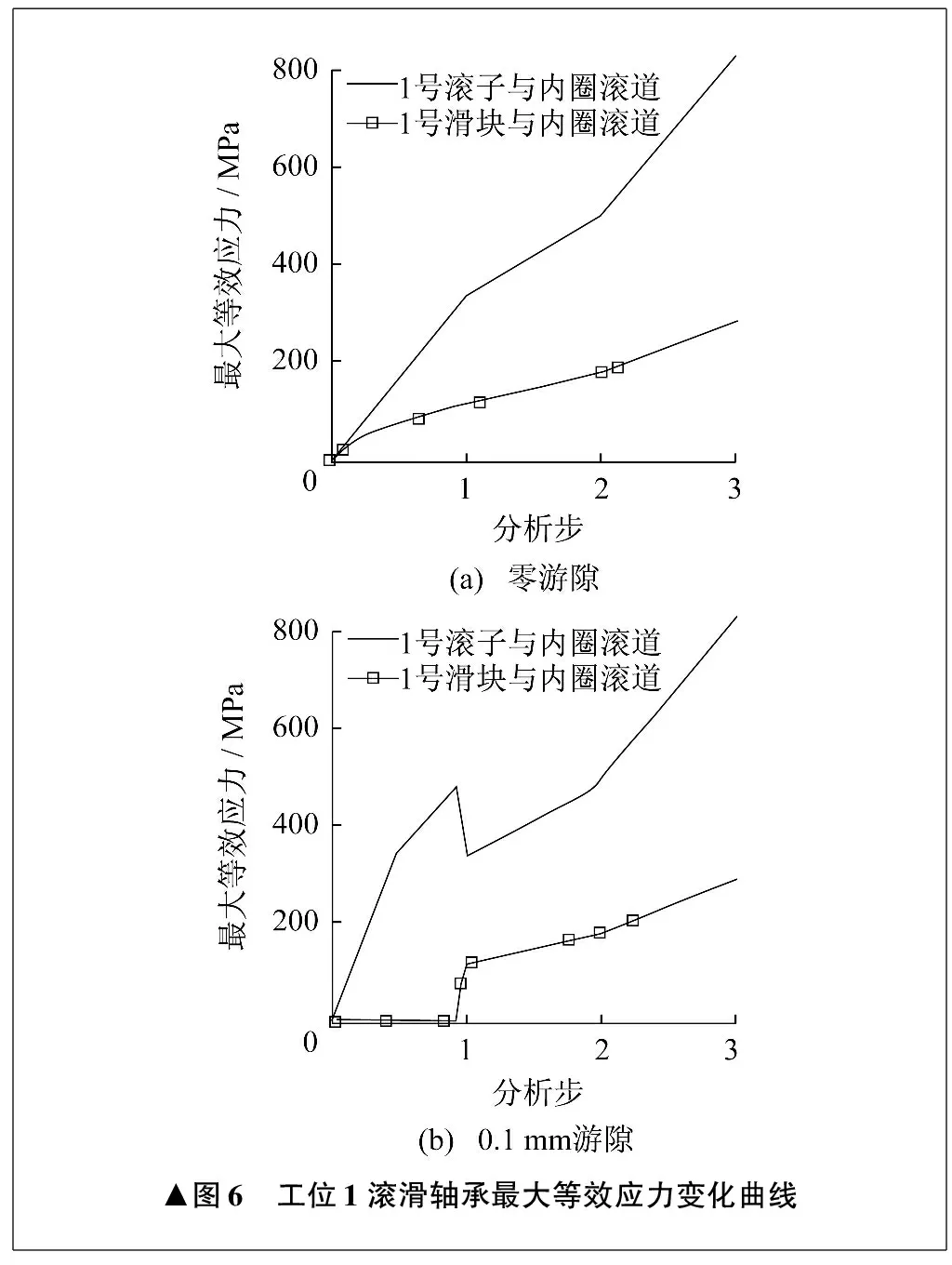
▲图6 工位1滚滑轴承最大等效应力变化曲线

通过上述分析可见，滑块受载的临界载荷显然与游隙有关。对于工位1,在0.05 mm游隙时,1号和2号滑块承受的临界载荷为11 375 N,3号滑块承受的临界载荷为11 518 N,4号滑块承受的临界载荷为12 051 N;在0.15 mm游隙时,1号和2号滑块承受的临界载荷为12 402 N,3号滑块承受的临界载荷为12 480 N,4号滑块承受的临界载荷为12 610 N;在0.30 mm游隙时,1号、2号和3号滑块承受的临界载荷均为12 727 N,4号滑块承受的临界载荷为12 805 N。对于工位2,在0.05 mm游隙时,1号、2号和3号滑块承受的临界载荷为11 440 N,4号滑块承受的临界载荷为11 895 N,5号滑块承受的临界载荷为11 960 N;在0.15 mm游隙时,1号滑块承受的临界载荷为12 191 N,2号滑块承受的临界载荷为12 402 N,3号和4号滑块承受的临界载荷为12 532 N,5号滑块承受的临界载荷为12 686 N;在0.30 mm游隙时,1号、2号和3号滑块承受的临界载荷均为12 740 N,4号滑块承受的临界载荷为12 753 N,5号滑块承受的临界载荷为12 818 N。

由此可以看出,游隙大小影响滑块承受的临界载荷,游隙越大,滑块承受的临界载荷越大。相同游隙时,对于两种典型工作位置，均是1号滑块承受的临界载荷最小。对于工位1，4号滑块承受的临界载荷最大,2号和3号滑块承受的临界载荷大于或等于1号滑块,小于4号滑块。对于工位2，5号滑块承受的临界载荷最大,2号、3号和4号滑块承受的临界载荷大于或等于1号滑块,小于5号滑块。

为了进一步研究游隙对滚滑轴承性能的影响,为滚滑轴承的游隙选择和结构优化提供理论参考,给出工位1时1号滚子在不同游隙时的最大等效应力变化曲线,如图7所示。

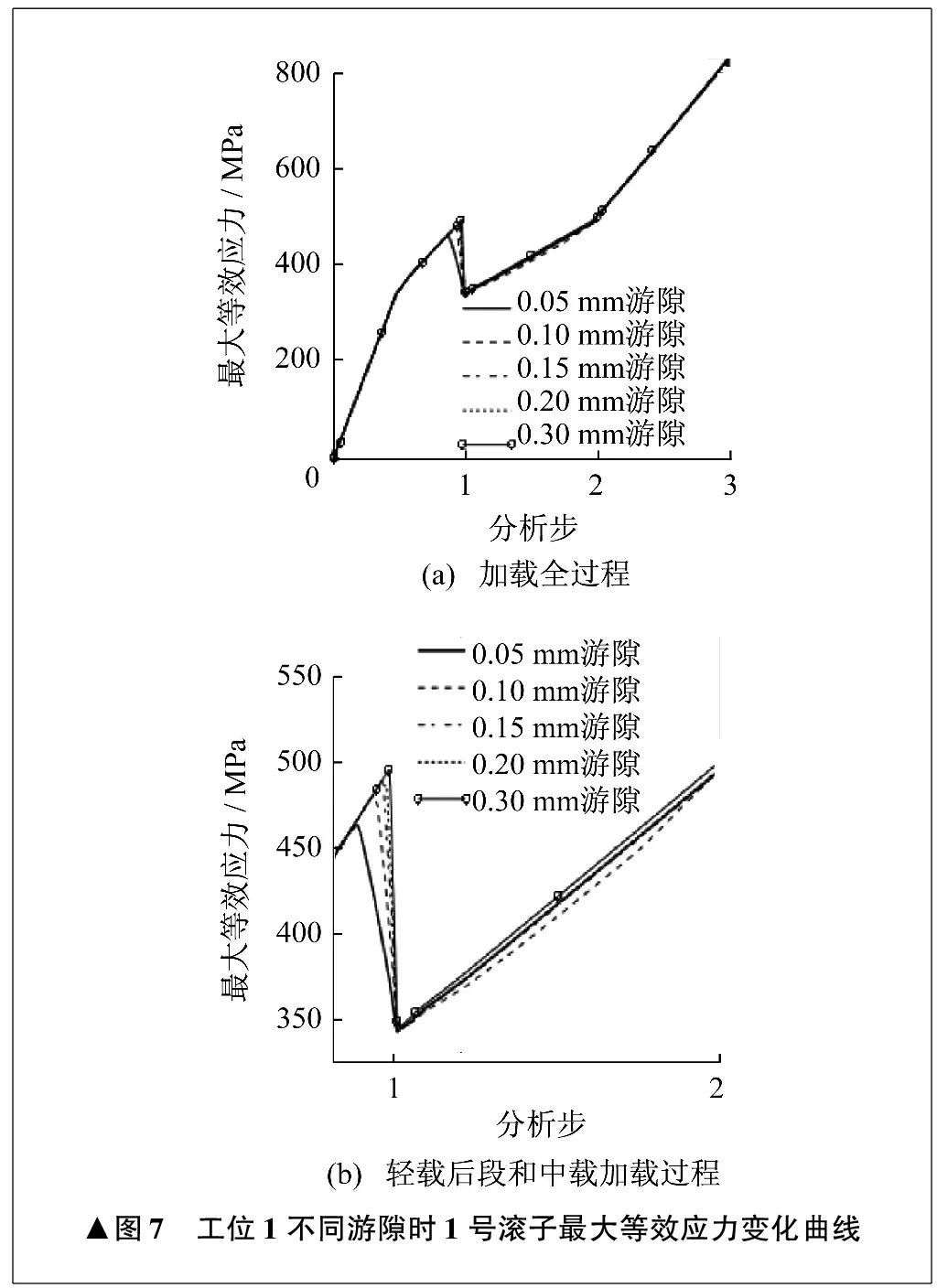
▲图7 工位1不同游隙时1号滚子最大等效应力变化曲线

由图7可知,轻载时,游隙越大,1号滚子的最大等效应力越大。当外部载荷为临界载荷时，1号滚子的最大等效应力快速减小。中载时,1号滚子的最大等效应力在0.1 mm游隙时小于其它几种游隙。在0.3 mm游隙时，1号滚子的最大等效应力最大。重载时，游隙对1号滚子最大等效应力的影响不明显。其它受载滚子最大等效应力在不同游隙时的变化规律与1号滚子基本一致。综合游隙对滚滑轴承内部载荷和应力分布的影响,在具体情况下,取游隙为0.1 mm较好。

4 结论

通过研究游隙对滚滑轴承内部载荷及应力分布的影响,可以得到以下结论:

(1)滑块与内、外圈滚道之间的载荷大于滚子与内、外圈滚道之间的载荷，滚子的最大等效应力大于滑块的最大等效应力；

(2)滚子和滑块与内、外圈滚道接触的端部都存在边缘效应；

(3)游隙影响滚滑轴承内部载荷分布,使滑块承受载荷的最小外部径向载荷称为滑块承受的临界载荷，游隙越大,临界载荷越大；

(4)在滚滑轴承外部载荷小于临界载荷时,滑块不承受载荷,因而说明游隙可改善轴承的启动性能；

(5)游隙影响应力分布,外部载荷大小不同，游隙对滚滑轴承内部等效应力的影响有所不同,外部载荷越大,游隙对最大等效应力的影响越小。