巧用“一线三等角”模型突破数学综合题

曾静

【摘要】利用MM策略数学建模思想是重要的教与学的思想，灵活掌握和应用数学模型解题是解决综合题型的重要突破方法。巧用“一线三等角”模型能更好地突破数学综合题，拓宽学生的解题思路，拓展学生的解题思维，让学生获取学习数学的灵性，让学习数学变得更有趣。现代数学理念认为数学教学是数学思维过程的教学。数学教学不仅要使学生获得新的知识，而且要提高学生的思维能力，要培养学生自觉运用数学知识考虑和处理实际问题，从而形成良好的思维品质。

【关键词】数学建模思想;一线三等角模型;数学综合题

数学课标实验本在前言部分11次提到了数学的建模，用模问题，数学建模的思想对提高初中生数学思维能力有很大的促进作用，它能使学生真正把数学学会学活，达到深化、理解知识、发展应用数学的思维能力，促进数学素质的提高。

利用数学模型思想，让教师们在教学中不只为讲一个知识点或讲一道题进行按点教学，而是按块教学。运用综合知识解决一类有共性的题，归纳出模型，利用模型思想解决更多的一系列题。利用数学模型思想教学应该渗透到平时的实际教学中，这样能提高学生们的数学思维能力，让学生在面对综合题时不会束手无措。模型思想的形成，可以给学生提供更合适的解题思路，减低学生的思维量，提高解题信心，缓解学生解题的紧张感，让数学综合题迎刃而解。

如何提高初中生数学思维能力是一个涉及面较大的综合性课题，目前，在教学理论界利用MM策略提高初中生数学思维能力这方面的研究还比较薄弱，我们正在开展这项课题研究，有利于发展和丰富学生数学问题解决能力。

学生到了九年级，数学知识累积到了一定程度，但很多知识理解和运用都比较模糊，尤其是对于解决综合题时更是无从下手。数学模型思想的学习，模型的应用在一定程度上能开拓学生的解题思路，在独立解题时能更好地引导自己进行解题突破，当学生一旦发现题目有熟悉感，离解题成功也就不远了。

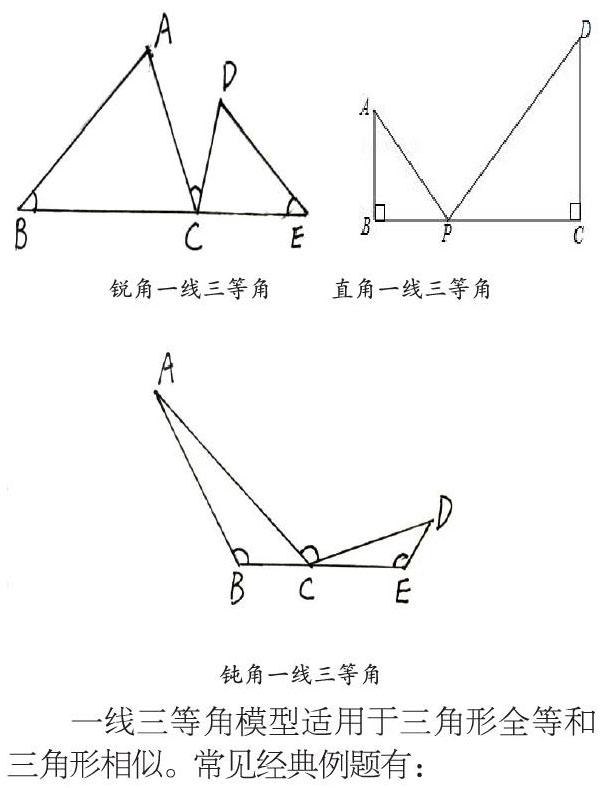
在大量的数学几何模型中，一线三等角模型使用较为广泛，在综合题中起到关键的解题突破的作用。一线三等角模型突出的特点就是构造两组角对应相等。具体的定义是：两个相等的角一边在同一条直线上，另一边在该直线的同侧或异侧，第三个与之相等的角的顶点在前一组等角的顶点中所确定的线段上或线段的延长线上，另外两边分别位于一直线的同侧或异侧与两等角两边相交，会形成一组相似三角形，习惯上把该组相似三角形称为“一线三等角型”相似三角形。（通俗地讲，一条直线上有三个相等的角一般都会存在相似三角形。）较常见的“一线三等角型”按角分，分别有“锐角一线三等角”“直角一线三等角”“钝角一线三等角”，三种模型如下图。

一线三等角模型适用于三角形全等和三角形相似。常见经典例题有：

求证：

“一线三等角”几何模型中，直角“一线三等角”模型尤为常用。它可以巧妙地穿插在函数和四边形等综合几何题中。此模型的熟練掌握通常能顺利帮助学生攻破综合难题。

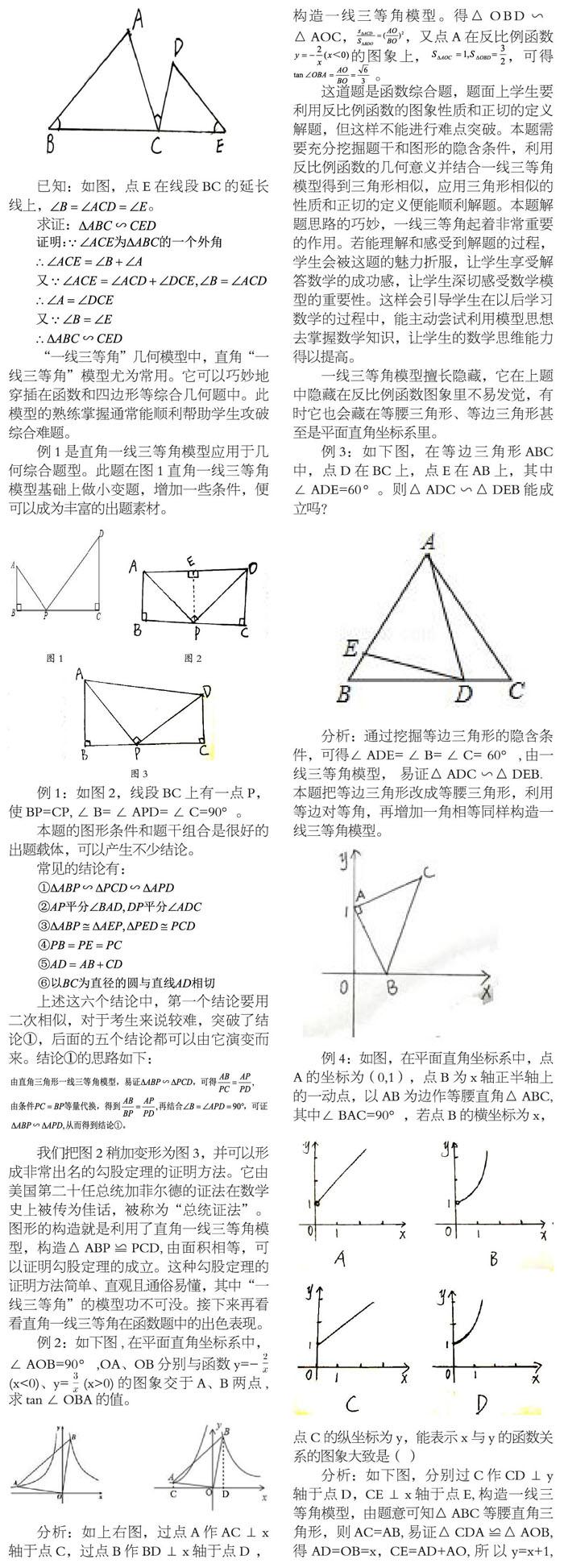
例1是直角一线三等角模型应用于几何综合题型。此题在图1直角一线三等角模型基础上做小变题，增加一些条件，便可以成为丰富的出题素材。

例1：如图2，线段BC上有一点P，使BP=CP，∠B=∠APD=∠C=90°。

本题的图形条件和题干组合是很好的出题载体，可以产生不少结论。

常见的结论有：

上述这六个结论中，第一个结论要用二次相似，对于考生来说较难，突破了结论①，后面的五个结论都可以由它演变而来。结论①的思路如下：

我们把图2稍加变形为图3，并可以形成非常出名的勾股定理的证明方法。它由美国第二十任总统加菲尔德的证法在数学史上被传为佳话，被称为“总统证法”。图形的构造就是利用了直角一线三等角模型，构造△ABP≌PCD，由面积相等，可以证明勾股定理的成立。这种勾股定理的证明方法简单、直观且通俗易懂，其中“一线三等角”的模型功不可没。接下来再看看直角一线三等角在函数题中的出色表现。

例2：如下图，在平面直角坐标系中，∠AOB=90°，OA、OB分别与函数y=-（x<0）、y=（x>0）的图象交于A、B两点，求tan∠OBA的值。

分析：如上右图，过点A作AC⊥x轴于点C，过点B作BD⊥x轴于点D ，构造一线三等角模型。得△OBD∽

△AOC，，又点A在反比例函数的图象上，，可得 。

这道题是函数综合题，题面上学生要利用反比例函数的图象性质和正切的定义解题，但这样不能进行难点突破。本题需要充分挖掘题干和图形的隐含条件，利用反比例函数的几何意义并结合一线三等角模型得到三角形相似，应用三角形相似的性质和正切的定义便能顺利解题。本题解题思路的巧妙，一线三等角起着非常重要的作用。若能理解和感受到解题的过程，学生会被这题的魅力折服，让学生享受解答数学的成功感，让学生深切感受数学模型的重要性。这样会引导学生在以后学习数学的过程中，能主动尝试利用模型思想去掌握数学知识，让学生的数学思维能力得以提高。

一线三等角模型擅长隐藏，它在上题中隐藏在反比例函数图象里不易发觉，有时它也会藏在等腰三角形、等边三角形甚至是平面直角坐标系里。

例3：如下图，在等边三角形ABC中，点D在BC上，点E在AB上，其中∠ADE=60°。则△ADC∽△DEB能成立吗？

分析：通过挖掘等边三角形的隐含条件，可得∠ADE=∠B=∠C= 60°，由一线三等角模型， 易证△ADC∽△DEB.本题把等边三角形改成等腰三角形，利用等边对等角，再增加一角相等同样构造一线三等角模型。

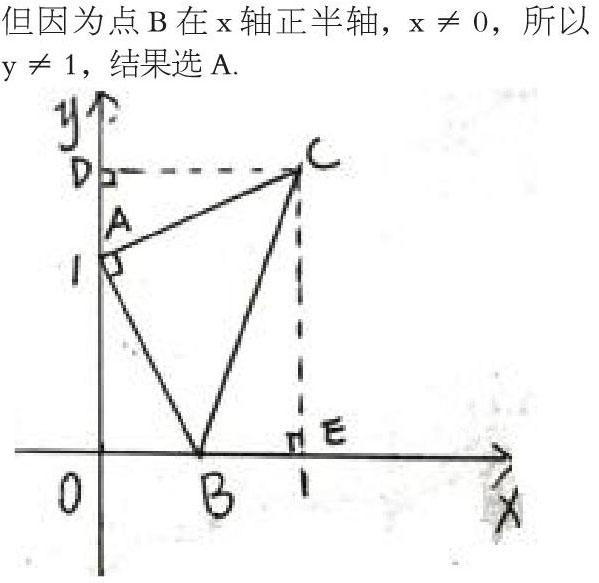
例4：如图，在平面直角坐标系中，点A的坐标为（0，1），点B为x轴正半轴上的一动点，以AB为边作等腰直角△ABC，其中∠BAC=90°，若点B的横坐标为x，点C的纵坐标为y，能表示x与y的函数关系的图象大致是（ ）

分析：如下图，分别过C作CD⊥y轴于点D，CE⊥x轴于点E，构造一线三等角模型，由题意可知△ABC等腰直角三角形，则AC=AB，易证△CDA≌△AOB，得AD=OB=x，CE=AD+AO，所以y=x+1，但因为点B在x轴正半轴，x≠0，所以y≠1，结果选A.

从例2和例4我们发现，一线三等角模型常应用在综合的数学题里，它不但便于解决相似问题，而且同样可以解决全等问题。一线三等角模型能提供三个相等的角，可以提炼出两组角对应相等的条件，若能结合题意找到任意一组边对应相等，三角形全等便成立了。总而言之，有边相等证全等，没边相等证相似。

数学教学的根本仼务在于教会学生如何学习、如何思考问题、如何应用知识解决实际问题，数学教师应该教育自己的学生学会把实际问题转化为数学问题加以解决，即建立数学模型。也许很多教师都会抱怨学生知识不能学以致用，分析和解决实际问题的能力差，其实这跟我们平时的教学有很大的关系，我们在平时的实际教学中，忽略了培养学生数学模型思想，学生没有建模意识，做题不能举一反三，哪怕再多的题海战术，都不能收到想要的学习效果。

数学模型策略（mathmaticatmodellingmethod），简称为MM策略，就是把一个现实原型引向我们熟悉的模型.原有的熟悉模型经过推广，从而来解决一类具有公共特点的数学问题，提高学生的解题能力。初中数学教学中此策略过程一般可分为抽象、推理、类比、发散、创新五个阶段。对于初中生而言，模型思想可能较难，不能一蹴而就，在教学中要循序渐进慢慢渗透，并引导学生在做题中实践应用。数学教学中让学生参与经历将问题加以提炼，抽象为数学模型，探究出利用模型解題的通性通法，验证模型的实用性，通过数学建模活动提高初中生数学思维灵活性、敏捷性、批判性和独创性等能力。

培养初中生“数学建模”的核心素养的研究，旨在从学生学习和发展的角度出发，以数学建模为突破点，从而提升学生的数学核心素养。数学建模既是学生学习的数学思想方法，也是学生学习数学知识、解决问题的一种能力。学生亲自经历模型建立的“再创造”过程，有助于培养学生初步学会运用数学的思维方式去观察和分析现实社会，解答日常生活中的问题，进而形成通于探索、勇于创新的科学精神，灵活地运用代数方法解决几何问题是值得研究和探索的。掌握正确的技巧和重视方法总结，往往事半功倍。数学看似变化莫测，实则很多题都可以抽象出基本模型。抓住模型，抓住本质，方能以不变应万变。当然，一切方法都建立在一定的知识基础上，打好基础才能更有效地学习。

在中考科目中，数学最能体现差距，作为数学的教育工作者，帮助学生提高数学思维能力是我们的必修课，有利于提高学生学习数学的兴趣，有利于提高学生的数学成绩，同时又可以减轻学生学习的负担，最大限度地开发学生的潜能，达到提高学生数学思维能力的目的。

参考文献：

[1]裴娣娜.教育研究方法导论[M].安徽教育出版社，1995，8.

[2]袁振国.教育研究方法[M].高等教育出版社，2000，7.

[3]张志存.例谈方程思想在解题中的应用[J].中国教育与教学，2006（10）：4.

[4]全国数学建模工作委员会.初中生数学建模能力培养教程[M].济南出版社，2014，9.

[5]猿辅导.中考必会几何模型[M].地质出版社，2017，12.