基于等维递补灰色模型的人口预测分析

唐贤芳，崔 岩，张淑丽

(西北工业大学明德学院信息工程学院，陕西西安 710124)

0 引言

一个国家或地区的人口数量直接影响该地区就业、环境、经济的发展，因此科学地预测人口的数量对制定经济政策、区域发展规划具有非常重要的意义[1].

灰色理论是邓聚龙教授于1982年提出的，GM(1,1)模型是其中内容之一，它具有所需信息量少，模型建立较简单，求解容易等特点，在社会、经济、农业、电力等领域得到了广泛的应用.但它也存在一些缺陷，比如对数据序列有比较严格的要求，当发展系数的绝对值比较大时，会使模型预测偏差增大，预测效果不理想.针对它的缺陷，近年来不少学者对GM(1,1)模型进行了改进[2].本文在数据检验的基础上，选择2003～2015年数据进行静态灰色建模，采用等维递补的方法对数据进行动态预测.对比两个模型，动态预测的效果明显优于静态预测.最后用构建的动态灰色预测模型对陕西省2018～2028年人口数量进行预测.结果可为有关部门制定相关决策提供了较为科学、合理的依据.

1 GM(1,1)模型的建立

1.1 静态GM(1，1)模型

GM(1,1)灰色模型是通过对原数据进行生成处理，使其呈现指数变化趋势，依此建立微分方程，得到预测模型.该模型适用于对部分信息已知、部分信息未知的灰色系统进行预测，特别适合小样本、增长速度较快的数据建模求解[3].它的建模一般分为以下几个步骤.

第一步：原始数据检验.因为GM(1,1)本质是指数方程，为了确保建模的可行性，要求用于预测的数据具有指数变化规律，才能建立灰色模型.数据检验的标准有级比检验和光滑度检验两种.

设原始数据列为

x(0)=[x(0)(1),x(0)(2),…,x(0)(n)]

(1)

级比检验：定义数据序列的级比为

(2)

光滑度检验：首先对原始数据序列做一次累加，生成累加序列为

x(1)=[x(1)(1),x(1)(2),…,x(1)(n)]

(3)

(4)

是k的递减函数，则该数据序列为光滑离散序列.只有满足这一条件才适合用灰色预测.

第二步:灰色模型的建立.对累加序列建立一阶微分方程

(5)

其中α是发展灰数，μ为内生控制灰数.

第三步:灰色模型的求解.设取背景值z(1)(k)为x(1)的邻近均值生成数序列

z(1)(k)=0.5[x(1)(k-1)+x(1)(k-1)],

k=2,3…,n

(6)

(7)

其中

Y=[x(0)(2),x(0)(3),…,x(0)(n)]T

(8)

将求解出的参数代入到微分方程(5)中，得相应的x(1)序列预测模型为

k=1,2,…n-1

(9)

累减后得到原始数据序列的预测为

k=1,2,…n-1

(10)

第四步：模型精度检验.为了确保所建立的灰色模型有较高的精度能够应用于预测实际，按照灰色理论需要对所建立的GM(1,1)模型的精度进行检验.一般的精度检验包括3个方面：残差检验、关联度检验和后差检验[4].

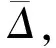
(10)

一般要求相对残差值小于20%，最好是小于10%，符合要求.

关联度检验: 关联度是用来定量描述各变化过程之间的差别.关联系数越大，说明预测值和实际值越接近.第t个数据的关联系数定义为

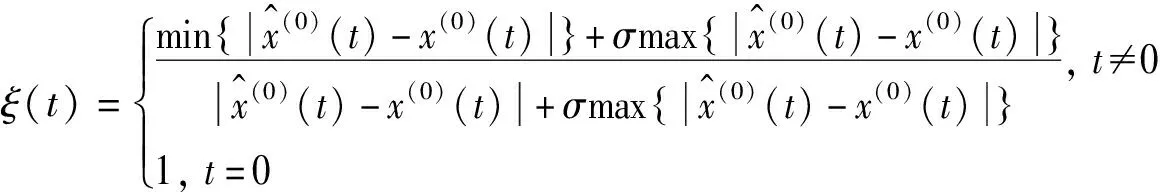
(11)

(12)

当关联度的值大于0.6时，认为通过检验.

后验差检验: 后验差检验有两个指标，即后验差比C和小误差概率P.

(14)

其中S1,S2分别为原始数据和残差的均方差.模型精度等级参考表1所示.

表1 后验差检验判别参照表

1.2 等维递补动态GM(1,1)模型

等维递补模型是对传统静态GM(1,1)模型的动态应用，它通过不断引入已知信息来减少灰平面的灰度，这样的模型由于及时引入了新的已知信息，就能比较准确及时地反映系统的变化.它的原是用已知数列建立第一个灰色模型，用它来预测第一个预测值.然后将第一个已知的值去掉，将预测值加到数列后，保持数据序列的等维，然后重新建立灰色模型，预测下一个值.如此推进、重复，逐个预测、去值、递补，直到完成预测任务或达到精度要求[5].

2 陕西省人口预测的实证分析

2.1 数据搜集与处理

灰色预测的特长是样本数据不必很多，即“小样本”数据，所以样本的选取不需太多.通过查询中国统计网的数据中心，选取2003～2017年陕西省年末人口总数为预测样本，具体值见表2.

选取2003～2015年数据建立静态灰色模型，

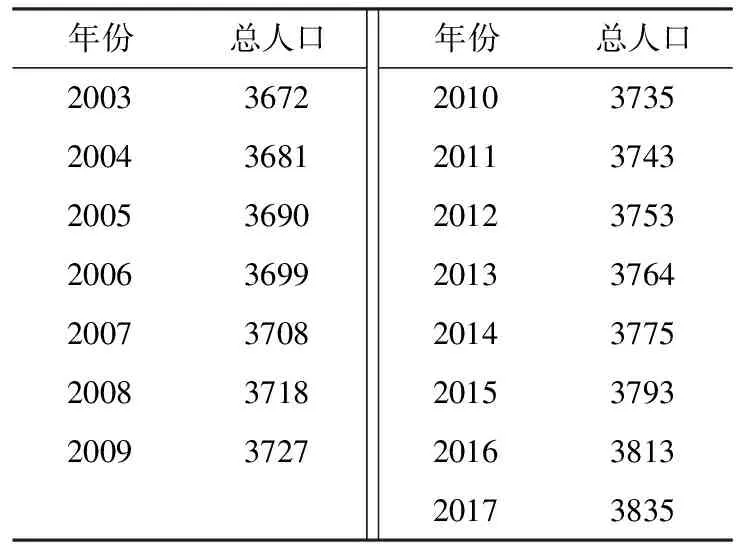
表2 2003～2017年陕西省人口数(单位：万人)

根据公式(1)得到

x(0)=(3672,3681,3690,3699,3708,3718,3727,3735,3743,3753,3764,3775,3793)

按照建模过程，则对上式进行一次累加生成，根据公式(3)得到新序列:

x(1)=

2.2 数据检验

对数据进行级比检验.根据公式(2)计算得

δ(k)=

当n=13时，

表明原始数据满足级比检条件.

根据公式(4)，则

ρ(k)=(1.0025,0.5018,0.335,0.2515,

0.2015,0.1681,0.1442,0.1263,0.1125,0.1014,

0.0923,0.0849),

满足数据光滑度检验要求.检验结果表明原始数据序列可以用于GM(1,1)灰色模型预测.

2.3 静态GM(1,1)灰色模型

根据公式(7)计算灰色系数α,μ:

将系数代入公式(8)得到GM(1,1)一次累加数据的预测模型为

(13)

取k=1,2…,14，利用式(13)计算出2003～2017年的一次累加数据，再利用公式(9)计算2003～2017年陕西省人口预测值，见表3第3列.

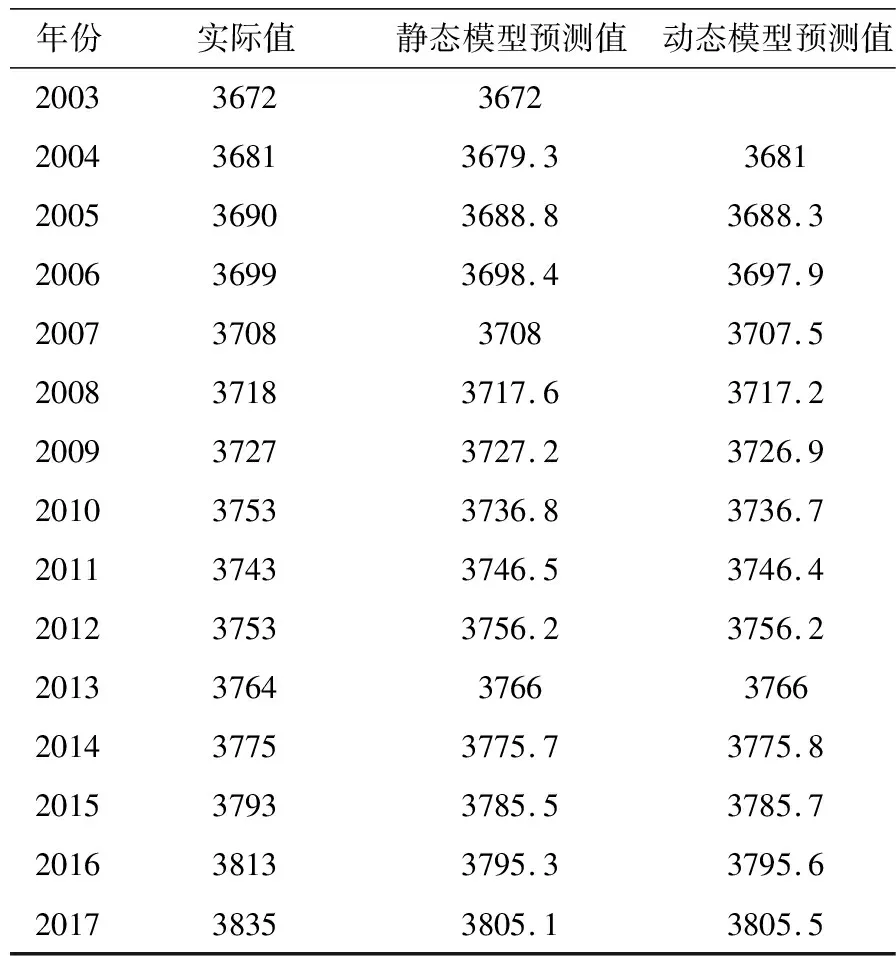
表3 拟合及人口预测

2.4 等维递补GM(1,1)预测模型

为了降低灰度，对预测样本采用逐年递补，不断补充新信息，对静态GM(1,1)模型参数做不断修正，通过一次递补预测2017年陕西人口数量.递补GM(1,1)预测模型的原始预测数据列为

累加数据预测模型

对以上两种模型预测结果，进行残差检验、关联度检验和后差检验，结果见表4.

表4 两个模型检验值

从表4可见，两个模型的精度都满足要求，可以进行外推预测，但动态模型的精度更高.且从预测的2017年的数值可见，动态预测数值比静态预测的数值更接近真值.所以，选择动态模型进行外推预测.

根据灰色预测维数选择经验：数据年份越靠近待预测年份预测越准确.我们选择2005～2017年数据运用等维递补方法进行外推.通过MATLAB编程计算得到陕西省2018～2028年的人口预测值，见表5.

对于以上外推模型进行残差检验、关联度检验和后差检验，检验结果如表6所示.

从表6可见，预测2018～2028年的模型精度均为优，从各项综合指标来分析，精度随着外推的次数呈现先增后减的趋势，第十次外推的后验差值比较高，所以，不再往外递推.

表5 2018～2029年陕西省人口预测值(单位：万人)

表6 外推模型的精度检验

3 结论

(1)选择一样的数列进行预测，动态递补模型明显好于静态预测，预测精度更高，可靠性更强；

(2)采用动态递补预测，随着模型的外推，精度会呈现先增后减趋势.递推次数不能太大，一定要结合精度要求综合考虑；

(3)根据动态预测结果，陕西省人口呈现递增趋势.但每年增加的比例在0.35%左右，与陕西省人民政府印发的人口规划中，提到人口自然增长率稳定在0.4%有些差距，需要相关部门采取措施提高人口自然增长率.