基于随机Kaczmarz算法的最小二乘拟合
杨 红,陈豫眉
(西华师范大学 a.数学与信息学院; b.公共数学学院, 四川南充 637009)
0 引言
随机Kaczmarz算法(简称RK算法)[1]是目前求解大型超定线性方程组的经典方法之一,当系数矩阵的行数大于矩阵的列数的三倍时,该算法甚至优于著名的共轭梯度算法.2009年,Strohmer和Vershynin提出了依指数线性收敛的RK算法[1].随后,一些学者对RK算法的补充证明[2-6]进一步说明了该算法的收敛性.RK算法利用交替投影的方法进行迭代,由于其算法简单,运行速度非常快,被广泛应用到了许多实际问题中,如数字信号处理、X射线断层扫描、图像重构等[7-9].
最小二乘法是一种优化方法,它通过最小化残差平方和来寻找适合数据的最佳匹配函数.最小二乘拟合在数据预测方面有着重要应用,如化学、物理模型中的参数估计[10-13]等.最小二乘拟合求解方法有很多,最常用的如SPSS、MATLAB中的拟合工具箱[14-15]等.2010年,刘佳琪等提出利用进化算法求解最小二乘拟合[16];2011年,颜清等提出利用EXCEL中的蒙特卡罗算法和VBA混合编程进行最小二乘拟合[17].当实验数据庞大时,最小二乘法拟合的实质是求解超定线性方程组.目前已有的最小二乘拟合的求解方法,在一定程度上虽能达到较好的拟合效果,但当实验数据庞大时,将面临计算量大的困难.因此, 本文利用求解大型超定线性方程组的RK算法进行最小二乘拟合,以更好地应用于实际问题.
1 最小二乘法理论
最小二乘法起源于天文学和地理测量学的研究.1805年,勒让德在其论著《计算慧星轨道的新方法》中给出了最小二乘法清晰且简明的阐述.1809年,高斯在《关于绕日行星运动的理论》中也提出了最小二乘法.下面给出最小二乘法的一般理论.
设有一组实验数据(xi,yi),i=1,2,...,m,最小二乘拟合即求函数f(x)使得
(1)
用最小二乘法拟合曲线,可根据给定数据散点图确定拟合函数f(x)的形式.一般地,设待求函数f(x)属于函数空间
φ=span{φ1,φ2,…,φn},
即f(x)可由函数φj,j=1,2,…,n的线性组合表示
故式(1)等价于求解
(2)


则式(2)等价于求解
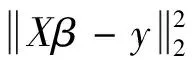
(3)

当函数空间φ=span{1,x,x2…,xn}时,即为常用的最小二乘多项式拟合.
2 基于RK算法的最小二乘曲线拟合
2.1 RK算法
给定超定线性方程组
Ax=b,
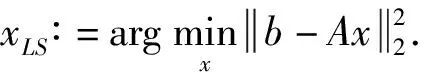
RK算法[1]通过正交投影建立相应的迭代公式来求解超定线性方程组.下面给出其主要思想.

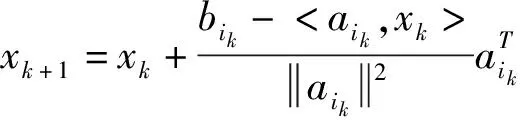
其中ik∈{1,2,...,m}是根据上述概率随机选择得到的行指标.
其算法步骤为
1)输入超定线性方程组中的系数矩阵A和右端列向量b;
2)规定最大迭代次数K,赋迭代次数初值k=0,赋迭代初值x0;
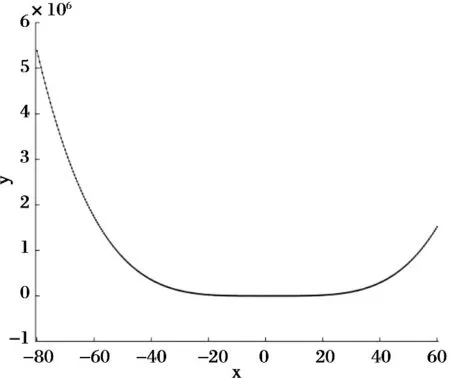
3)当迭代次数k 6)更新迭代次数k=k+1,返回步3. 给定函数f(x)∈φ=span{φ1,φ2,...,φn},对已知的实验数据(xi,yi),i=1,2,...,m进行拟合.将实验数据带入拟合函数f(x)得到一个超定线性方程组 Xβ=y (4) 其中X是m×n阶矩阵,y是m×1阶向量,β是n×1阶向量.本文将通过RK算法计算出拟合参数向量β. 当实验数据庞大时,式(4)是一个大型超定线性方程组,RK算法求解大型超定线性方程组时具有依期望指数收敛的性质,故用RK算法进行最小二乘拟合. RK算法中涉及随机因素,为了避免随机产生的影响,将数值实验运行50次所得平均值作为最终结果.设算法中规定的最大迭代次数K=20000,实验运行环境为MATLAB R2018a. 文中利用的拟合相关系数计算公式为 例1 利用RK算法对表1中的实验数据进行最小二乘直线拟合. 表1 直线拟合的实验数据 拟合函数表达式为f(x)=β1+β2x,将实验数据带入该表达式,得到如下超定线性方程组: 令 通过RK算法计算得(β1,β2)=(-2.0365,22.7982),R2≈0.9984,拟合效果好. 例2 利用文献[17]中给出的化工动量传递和热量传递的实验数据,拟合传热准数经验关联式. 表2 化工动量传递和热量传递的实验数据 传热准数经验关联式由普兰德数Pr、雷诺尔数Re和努塞尔数Nu三个参数控制,其表达式为 Nu=aRemPrn. 对于这个非线性函数的拟合,两边取以10为底对数,得到 lgNu=lga+mlgRe+nlgPr 将实验数据带入上述表达式,得到一个超定线性方程组.通过RK算法计算得参数a=0.1193,m=0.6628,n=-0.3220.计算该曲线拟合的相关系数R2≈0.9999,高于文献[17]中利用蒙特卡罗拟合得到的相关系数R2≈0.9985.可见RK算法进行最小二乘数据拟合有一定的优势. 图1 测试数据散点图 图2为通过RK算法拟合曲线,拟合相关系数R2≈1.0000.此例中的拟合方程组个数为300,说明RK算法用于大型数据最小二乘拟合效果非常好. 图2RK算法拟合的曲线 最小二乘法的应用极其广泛,在数据拟合方面有着重要的作用.然而,当实验数据增多时,运用一般的方法进行拟合求解会产生庞大的计算量.本文将求解超定线性方程组的RK算法应用于最小二乘拟合,效果非常好.

2.2 基于RK算法的最小二乘拟合
3 数值实验及结果


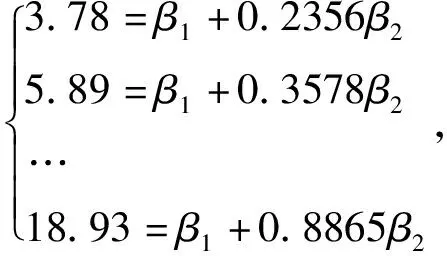



4 结语

