数学教学中的数学建模

吴庆丰

(淮北师范大学数学科学学院，安徽淮北 235000)

0 引言

数学建模(Mathematical Modeling)[1]：根据需要，针对实际问题，利用相关的数学知识，建立数学模型的全过程(包括表述、求解、解释、检验等).

数学建模可以理解现实世界到数学世界的“双向翻译”见图1.

表述:根据建模目的和信息将实际问题“翻译”成数学问题.

求解:选择适当的数学方法求得数学模型的解答.

解释:将数学语言表述的解答“翻译”回实际对象.

验证:用现实对象的信息检验得到的解答.

图1 模型框图

1 课堂设计想法和建议

1.1 教学要求

认真听讲，缜密思维；做好笔记，认真复习；积极讨论，完成作业；动手解决问题.

1.2 教学目的

掌握专业知识，有效培养应用所学知识解决实际问题的综合能力.

1)“双向翻译”能力；

2)运用数学思想进行综合分析能力；

3)结合其他专业特别是应用计算机解决问题的能力；

4)观察力和想象力；

5)提高撰写科研论文的能力；

6)团结协作的精神.

1.3 教学方式的多样性

教师讲授方式，小组讨论方式，学生报告方式数学.

1.4 教学课堂设计

在数学教学中，讲解理论专业知识结合实际应用，一方面从实际应用中更深刻领会专业知识，另一方面锻炼学生将专业的数学知识应用于实际问题的能力，让学生体会到数学知识不仅仅是枯燥的理论知识，也有广泛的实际应用.

有些问题课前可做好问卷调查,要求学生如实独立完成.对课堂教学的建议：争取尽可能多地互动，活跃气氛.特别希望任课老师能把自己在实践中发现的问题(优缺点、可行性的肯定或否定意见等)实话实说地提出来，一起进行分析研究，共同找出问题所在，提出具体的改进方法；除了课堂学习外, 要求学生亲自动手，认真作几个实际问题，(作业和课后练习——体验).

2 应用举例

运输问题[2]在现实中有着广泛的应用，是一类具有特殊结构的线性规划问题，由于其模型结构的特点，可以采用比单纯形法计算效率高得多的表上作业法求解.

例1设有三个供应地A、B、C向四个需求地Ⅰ、Ⅱ、Ⅲ、Ⅳ供应物资W.各物资数量,各地区年需要量及从各供应地到各需求地运送单位物资的运价(万元/万吨)如表1所示.试求出总运费最省的物资调拨方案.

表1 供求量及单位运价表

此问题是计算从3个发点到4个收点的最小费用运输问题.首先让学生看懂上述表格，从三个供应地A、B、C往四个需求地区Ⅰ、Ⅱ、Ⅲ、Ⅳ运送物资，每个供应地有供应量限制，每个需求地有最低需求和最高需求，其中地区Ⅳ最高需求为不限，向学生提问：不限是否意味地区Ⅳ最高需求是无限大的意思.有的学生没认真思考回答是的，纯粹从表格简单的看似乎是这样，但其实不是.另外有的学生经过认真思考回答不是，地区IV最多可得到(50+50+60)(总产量)-(70+30)(其它地区最小需求)=60.从C到Ⅳ为禁止，表示C不往Ⅳ运送物资，向学生提问：C不往Ⅳ运送物资在模型中应该如何处理？处理方式可以将C往Ⅳ的运输成本设为很大，此时运输方案如果选择从C往Ⅳ的运输量不为零，那么将受到惩罚使得运输费用很大就不可能为最省方案.

下面建立数学模型.决策变量xij表示从供应地i(i=1,2,3分别表示供应地A,B,C)往需求地j(j=1,2,3,4分别表示需求地Ⅰ,Ⅱ,Ⅲ,Ⅳ)的运量，单位为万吨.aij表示从3个供应地A、B、C到4个需求地Ⅰ、Ⅱ、Ⅲ、Ⅳ的每单位运输费用，单位为万元/万吨.pi表示3个供应地A、B、C的产量，gj,hj分别表示4个需求地Ⅰ、Ⅱ、Ⅲ、Ⅳ的最低、最高需求量，这里aij，pi，gj,hj均为已知量.向学生提问：最高需求、最低需求在模型中如何表达？学生经过思考回答：必须保证最低需求，在约束条件中是“≥”号，不得超过最高需求，在约束条件中用“≤”号表示.要求总运费最省，目标函数为

约束条件：首先保证需求地最低需求有

然后考虑不超过最高需求有

最后考虑每个供应地的实际运输量不超过其产量有

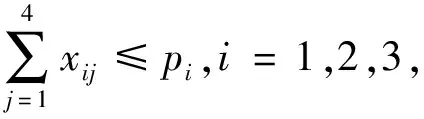
所以数学模型为

此问题是产销不平衡的运输问题，可以采用表上作业法求解.首先，需要将产销不平衡的运输问题化为产销平衡的运输问题，让学生思考并讨论如何将产销不平衡的运输问题化为产销平衡的运输问题？三个供应地总产量为160万吨，四个需求地的最低总需求量为110万吨，最高需求量为无穷大.根据现有产量，需求地Ⅳ最多分配60万吨，这样最高需求量为210万吨，大于总产量160万吨，为了得到平衡，在产销平衡表中增加一个假想的供应地D，其年产量为50万吨.由于各需求地的需求量包含两个部分，比如需求地Ⅰ最低需求量是30万吨，由于最低需求必须满足，故不能由虚拟供应地D供给，为了处理这个问题，可以令相应单位运价为M(任意大的抽象正数)，而另一部分需求量20万吨可以满足也可以不满足，因此可以由虚拟地D供给，注意此时令相应单位运价为0.要求学生思考总结处理方法，如何确定虚拟地往各需求地的单位运价，可以互相讨论.但凡需求分为两种情况的地区，实际上可以按照两个地区对待，如果需求必须满足，则供应不能由虚拟地供应(由于虚拟地是假想的实际不存在，仅是为了产销平衡)，此时令相应运价为M，如果需求不必满足，则可以由虚拟地供应，此时令相应运价为0.下面给出此问题的产销平衡单位运价表，如表2所示.

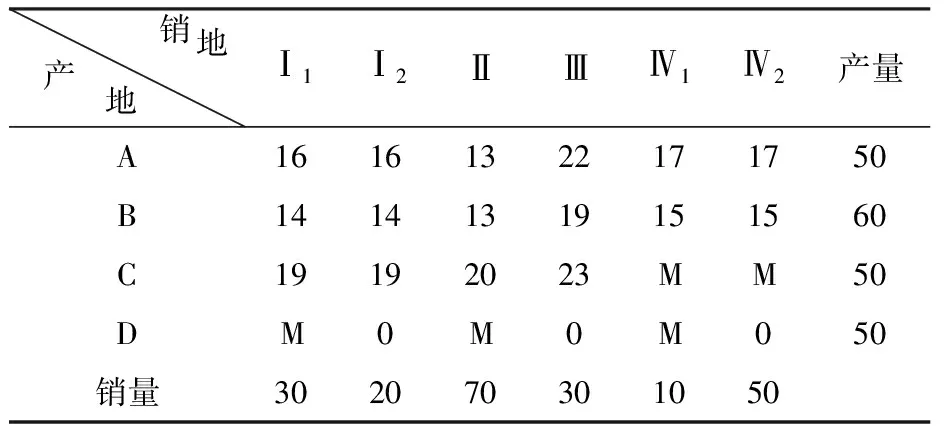
表2 产销平衡单位运价表

利用表上作业法求解可得最优运输方案如表3所示.

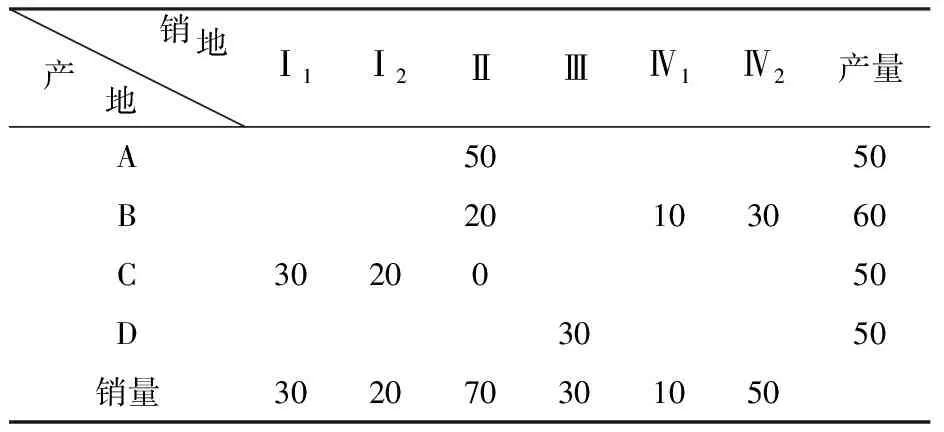
表3 最优运输表

此模型也是特殊的线性规划模型，可以借助数学软件LINGO求解，下面采用LINGO软件编程求解.

sets:

r/1..3/:p;!A,B,C 3个供应地的产量;

c/1..4/:g,h;!g,I,II,III,IV的最低需求, h,I,II,III,IV的最高需求;

m(r,c):x,a;!x,运输方案，a,运输成本;

endsets

data:

p=50 60 50;

g=30 70 0 10;

h=50 70 30 60;

a=16 13 22 17

14 13 19 15

19 20 23 1000; !c禁止往IV运输，设成很大的数;

enddata

min=@sum(m:a*x);

@for(c(j):@sum(r(i):x(i,j))>g(j);@sum(r(i):x(i,j))

@for(r(i):@sum(c(j):x(i,j))=p(i));

End

运行LINGO可知，全局最优目标值即总的最小运费为2460万元，最省运输方案为：A往II运输50万吨，B往II运输20万吨，B往IV运输40万吨，C往I运输50万吨.

此模型也可采用MATLAB编程求解，结合计算机求解,顺应了当前社会的发展,也使学生的综合能力得到提高.

3 结语

“创新是推动人类社会向前发展的重要力量”，[3]在数学教学中融入数学建模的思想，有利于培养学生创造性的思维能力，创造性的洞察能力和创造性的科研能力，这些都是创新人才所必备的能力.数学教学中融入数学建模顺应了当前素质教育和课程改革的需要.将理论知识应用于实际问题中往往内容的具有趣味性,有些问题就象是做游戏，引人入胜，更能激发学生的学习兴趣，又锻炼了学生动手解决实际问题的能力,体现了素质教育.