广东省2019年中考第24题解题思路与感悟

广东省鹤山市雅瑶中学

圆既是轴对称图形，又是旋转对称图形，具有旋转不变性，圆与其他章节知识点的联系非常密切，知识之间相互渗透，相互转化.与圆有关命题题材丰富，背景题材多样性，具有解法灵活且综合性强，可操作性强的特点，是各省市中考题必考的题型之一.

广州中考数学连续几年出现“结合图象”这四个字，说明函数教学中要引导学生重视画函数的图象，包括准确画出函数图象和画出函数的大致图象，通过函数图象，运用数形结合思想解决代数的数学问题.

波利亚说：“如果你想学会游泳，你必须下水；如果你想成为解题能手，你必须解题”.数学是严谨的科学，因此教师必须深入研究初中和高中教材，以教材为中心，加强对中考题的研究和思考，引导学生领悟出其中的解题方法、核心概念、基础知识所蕴含的基本性质、基本思想、基本方法，达到培养学生的高阶思维能力.

下面谈一谈广东省2019年中考第24题圆综合题解题思路和感悟.

题目如题24-1 图，在ΔABC中，AB=AC，⊙O是ΔABC的外接圆，过点C作∠BCD=∠ACB交⊙O于点D，连接AD交BC于点E，延长DC至点F，使CF=AC，连接AF.

(1)求证：ED=EC；

(2)求证：AF是⊙O的切线；

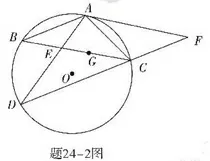
(3)如题2 图，若点G是ΔACD的内心，BC·BE=25，求BG的长.

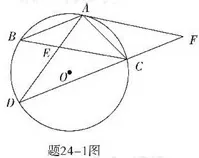
这题干文字精炼，图形外观简洁，问题由浅入深，内涵十分丰富.本题涉及的知识点有等弧对等角，相似三角形，平行四边形等知识.

(1)如图求证：ED=EC.

证法1如24-1-1 图所示：以圆为背景求证边相等，利用“等角对等边”易证得边相等.要证明DE=EC，只要证明∠2=∠4.根据已知与图图形分析可发现有同弧则可以知道等圆周角∠3=∠4，最后利用等量代换证得∠2=∠4.

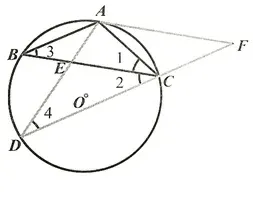
图24-1-1

证明如24-1-1 图，因为AB=AC，所以∠1=∠3.因为∠1=∠2，所以，∠2=∠3.因为∠3=∠4，所以，∠2=∠4，ED=EC.

证法2利用圆周角定理及已知条件推出同样易证得∠2=∠4，再利用等角对等边得出ED=EC.

证法3通过证明两三角形全等得两线段相等是证明两线段相等常用的方法，对于本小题证明ED=EC，也可以通过连结BD，证明ΔBDE∽= ΔACE也易证得ED=EC.

证法4由题目已知AB=AC，所以ΔABC为等腰三角形，由∠1=∠2，∠3=∠4，可证得ΔEDC∽ΔABC，所以ΔEDC为等腰三角形，即ED=EC.

证法5利用已知条件∠1=∠2,AB=AC得内错角∠2=∠3 相等，即可得AB与CD平行，易证得∠4=∠2，所以ED=EC.

感悟证明两线段相等的方法有：(1)证明三角形等角对等边；(2)证此两线段为全等三角形的对应边；(3) 用平行四边形对角线互相平分证明线段相等；(4)证此两条线段都等于第三条线段；(5) 证此两线段为同圆等弧所对的弦相等等.

(2)求证：AF是⊙O的切线；

证法1本题求证切线，已知点A在圆上，连半径证垂直即可，即证明∠OAF=90°，分别连结OB和OC，由垂直平分线逆定理得AO ⊥BC.再联系第一小题得内错角相等，两直线平行，证出平行四边形，便可利用平行证得垂直，顺利解题.具体证明过程如下.

证明如图24-2-1，连接OA,OB,OC,因为OB=OC,AB=AC,所以AO是BC的垂直平分线所以AO ⊥BC，因为由(1) 已证∠2=∠3，所以AB//DF，因为AB=AC=CF，所以 四 边 形ABCF是 平 行 四 边 形.所以AF//BC，AO ⊥AF,所以AF是⊙O的切线.

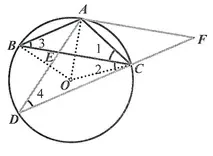
图24-2-1

证法2连接OB,OC,OA，通过全等得出OA垂直平分BC，再利用边角边定理得ΔBAC∽= ΔACF，由内错角相等得AF//BC，由平行得同位角相等，所以∠OAF=90°，即证得AF是⊙O的切线.

证法3如图24-2-3，连结AO交BC于点F，并延长AO交于圆于点M，则直径AM平分圆，即得由题目可知所以所以∠BAM=∠CAM，由三线合一得AM ⊥BC.同方法1 四边形ABCF是平行四边形得AF//BC，所以AO ⊥AF，所以AF是⊙O的切线.

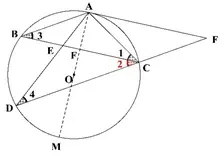
图24-2-3

证法4证明切线关键点在于证明过半径的外端且与半径垂直，我们想办法构建半径和90°.在圆的背景条件下构建90°，最常用的方法是用直径构直角三形角，这时，既有半径又有90°，通过转化思想把这个90°的圆周角转化到要证明的切线相关图形上.本题已知条件中没有出现直径，可以通过连结AO并延长AO交于圆于点M得到直径，再连结MC得到直径所对90°的圆周角，证明过程如下：

证明如24-2-4 图所示连结AO并延长AO交于圆于点M,连结MC.因为AM是直径，所以∠ACM=90°，所以∠M+∠5=90°.因为∠3=∠M，所以∠3=∠1.所以∠1=∠M.所以∠1+∠5=90°.所以AO ⊥BC,.由(1)得∠2=∠3，所以AB//DF.因为AB=AC=CF，所以四边形ABCF是平行四边形.所以AF//BC.AO ⊥AF,所以AF是⊙O的切线.

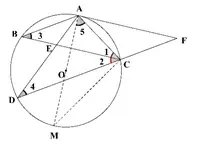
图24-2-4

感悟证明直线为圆的切线是中考的重要考点，要证明直线为圆的切线必须同时满足两个条件；(1) 经过半径的外端；(2) 垂直于半径.在证明一条直线为圆的切线时分两种情况：(1) 当已知条件中明确指出直线与圆有公共点时，常连接过该公共点的半径，证明该半径垂直于这条直线，可简单地说成“有交点，作半径，证垂直”本题以属于这种情况(2) 当已知条件中没有明确指出直线和圆是否有公共点时，常过圆心作该直线的垂线段，证明该线段的长等于圆的半径，可简单的说成“无交点，作垂线段，证半径”.

(3)如题24-2 图，若点G是ΔACD的内心，BC·BE=25，求BG的长.

解题思路由题目已知BC·BE=25的积式可以化为比例想到可能用三角形相似去求解.通常积式都是有一条边是两个三角形的公共边，我们沿着这个思路方向找出与线段BC和BE 相关又可以证明相似的两个三角形.点G是ΔACD的内心，它到三角形三边的距离相等，它与顶点的连线平分内角.但图中点G相对比较孤独，与内心相关的性质无法充分体现.通过连结AG，得出内心点G是∠DAC和∠ACD两个角的平分线的交点.最后利用等量代换便可以利用相似，具体的解题过程如下：

解如答24-3-1 图，连接AG,因为∠1 =∠2,∠2=∠5，所以∠1 =∠5.因为G是ΔADC的内心，所以∠7=∠8.因为∠BAG=∠5+∠7,∠6=∠1+∠8，所以∠BAG=∠6，所以AB=BG.因为∠3=∠3,∠1=∠5，所以ΔABE∽ΔCBA.所以25.AB=5.BG=5.

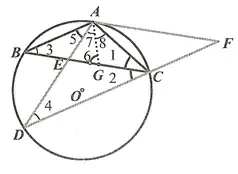
图24-3-1

感悟以圆为背景求线段长或线段的比，通常与勾股定理、垂径定理、全等三角形、相似三角形等知识的结合.解题过程中要重点关注观察已知线段间的关系，从中选择适当的解题方向，特别是要灵活进行弧、弦、角之间的相互转化，找出所求线段与已知线段的关系，从而化未知为已知解决问题.