含参广义集值平衡问题近似解映射的连续性

孟旭东

(南昌航空大学 科技学院，江西 南昌 330034)

诸多原始问题是近似问题的特殊情况，如著名的Eklands变分原理，它是处理近似解的基本规则.近似解的概念不仅适用于可行域为非凸集或非闭集的情形，而且它是数值计算的基础，如稳定性、适定性等. 论文近似解的概念是Loridan在文献[1]中讨论多目标规划问题时引入的.近年来，广义向量平衡问题引起了人们的广泛关注和研究兴趣，取得了阶段性的研究成果[2-10]. 论文受文献[1，9]思想的启发，在实拓扑向量空间中研究含参广义集值平衡问题近似解映射的连续性.

1 基本知识

设X,Y,Z为实拓扑向量空间,若对任何的t≥0,c∈C,有tc∈C，则称C⊂Z为凸锥.若C≠Z，则称锥C为正真的锥.若intC≠∅，则称锥C为立体锥.设C:X→2Z为具正真凸值的集值映射，对任何A⊂Z，记的A闭包为cl(A)，Z中的零元为0.

对每个(λ,ε)∈Λ×Ω，讨论两类含参广义集值平衡问题，分别记为(PGSVEP-1)和(PGSVEP-2).找x0∈K(λ)，使得

(PGSVEP-1)F(x0,y,λ)+ε⊄-intC(x0),∀y∈K(λ).

(PGSVEP-2) (F(x0,y,λ)+ε)∩(-intC(x0))=∅,∀y∈K(λ).

将(PGSVEP-1)与(PGSVEP-2)的近似有效解集分别记为Φ1(λ,ε),Φ2(λ,ε),即

Φ1(λ,ε)={x0∈K(λ):F(x0,y,λ)+ε⊄-intC(x0),∀y∈K(λ)},

Φ2(λ,ε)={x0∈K(λ):(F(x0,y,λ)+ε)∩(-intC(x0))=∅,∀y∈K(λ)}.

论文总假设对每个(λ,ε)∈Λ×Ω，Φ1(λ,ε)≠∅,Φ2(λ,ε)≠∅，旨在讨论Φ1(·,·),Φ2(·,·)在Λ×Ω上的连续性.

定义1[10]设X,Z为实拓扑向量空间，M⊂X为非空凸子集，C⊂Z为凸锥，f:M→Z为给定映射，则

(1) 称f在点x∈M处C-连续当且仅当对Z中零元的任何邻域V，存在x的邻域U，使得对任何的z∈U∩M，有f(z)∈f(x)+V+C.

(2) 称f在M上是C-连续的当且仅当f在M上的每一点皆C-连续.

定义2[8]设Z为实拓扑向量空间，C⊂X为立体凸锥，设W为Z的子集.称W为C-紧当且仅当对W中的任何覆盖{Wα+C:α∈I,Wα为Z中的开集,I为指标集}都有有限子覆盖.

定义3[5]设X为拓扑空间，Z为实拓扑向量空间，T:M⊂X→2Z{∅},C:M⊂X→2Z{∅}具有正真凸值的集值映射，设x0∈M，则

(1) 称T在x∈C(x0)处为C(x0)-下半连续当且仅当对Z中的任何开子集V，满足T(x)∩V≠∅，存在x的邻域U，使得T(u)∩(V+intC(x0))≠∅,∀u∈U.

(2) 称T在x∈C(x0)处为C(x0)-上半连续当且仅当对Z中的任何开子集V，满足T(x)⊂V，存在x的邻域U，使得T(u)⊂V+intC(x0),∀u∈U.

定义4[9]设X为具非空凸子集M的实拓扑向量空间，Z为实拓扑向量空间，T:M⊂X→2Z{∅},C:M⊂X→2Z{∅}具有正真凸值的集值映射，则

(1) 称T在M上为C-拟凹当且仅当对每个x1,x2∈M,z∈Z，满足T(x1)⊄z-intC(x1)，且T(x2)⊄z-intC(x2)，使得

T(x)⊄z-intC(x),∀x∈(x1,x2).

(2) 称T在M上为C-严格拟凹当且仅当对每个x1,x2∈M,z∈Z，满足T(x1)⊄z-intC(x1)，且T(x2)⊄z-intC(x2)，使得

T(x)⊄z-cl(C(x)),∀x∈(x1,x2).

定义5[9]设X为具非空凸子集M的实拓扑向量空间，Z为实拓扑向量空间，T:M⊂X→2Z{∅},C:M⊂X→2Z{∅}具有正真凸值的集值映射，则

(1) 称T在M上为C-真拟凹当且仅当对每个x1,x2∈M,z∈Z，满足T(x1)∩(z-intC(x1))=∅，且T(x2)∩(z-intC(x2))=∅，使得

T(x)∩(z-intC(x))=∅,∀x∈(x1,x2).

(2) 称T在M上为C-严格真拟凹当且仅当对每个x1,x2∈M,z∈Z，满足T(x1)∩(z-intC(x1))=∅，且T(x2)∩(z-intC(x2))=∅，使得

T(x)∩(z-cl(C(x)))=∅,∀x∈(x1,x2).

定义6[9]设X为拓扑空间，Z为非空子集，T,G:M⊂X→2Z{∅}为给定集值映射，称T为G的交叉映射当且仅当对每个x∈M，存在x的邻域U，使得

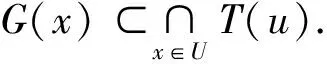
引理2[9]设X,Z为实拓扑向量空间，C:M⊂X→2Z{∅}具有正真凸值的集值映射，W:M⊂X→2Z{∅}为给定集值映射，且对任意的x∈M，W(x)=ZintC(x)有闭图，则C中至少有一个交叉映射，且具有立体凸锥值.

2 下半连续性

在以下假设条件下，讨论Φ1(·,·)与Φ2(·,·)在Λ×Ω上的下半连续性.

(A1) 设X,Y,Z为实拓扑向量空间，M⊂X,Λ⊂Y为非空子集，C:M→2Z{∅}为具正真凸值集值映射，F:M×M×Λ→2Z{∅},K:Λ→2X{∅}为给定集值映射；

(A2) 对每个(λ,ε)∈Λ×Ω，Φ1(λ,ε)≠∅；

(A3) 对每个(λ,ε)∈Λ×Ω，Φ2(λ,ε)≠∅；

(A4)K在Λ上具紧凸值；

(A5) 对每个λ∈Λ,y∈K(λ)，F(·,y,λ)在K(Λ)上为C-严格拟凹；

(A6) 对每个λ∈Λ,x∈K(λ)，F(x,·,λ)在K(Λ)上为C(x)-下半连续；

(A7) 对每个λ∈Λ,x∈K(λ)，F(x,·,λ)在K(Λ)上为C(x)-上半连续；

(A8) 对每个λ∈Λ,x∈K(λ)，F(x,·,λ)在K(Λ)上为C(x)-紧.

定理1假设(A1)，(A2)，(A4)～(A6)成立，则Φ1(·,·)在Λ×Ω上下半连续.

证明设(λ,ε)∈Λ×Ω，V为X中的开集，满足V∩Φ1(λ,ε)≠∅，x∈V∩Φ1(λ,ε).设x0∈V∩Φ1(λ,εμ),其中μ∈(0,1)，则

F(x0,y,λ)+με⊄-intC(x0),∀y∈K(λ)，

因此，有

F(x0,y,λ)+ε=F(x0,y,λ)+με+(1-μ)ε⊄-intC(x0),∀y∈K(λ)，

故x0∈V∩Φ1(λ,ε).

现取x*∈V∩{xθ∈K(λ):xθ=θx+(1-θ)x0},由(A5)，有

F(x*,y,λ)+ε⊄-cl(C(x*)),∀y∈K(λ).

任取y*∈K(λ)，则存在z(y*)∈Z，使得

z(y*)∈(F(x*,y*,λ)+ε)∩(-cl(C(x*)))c.

由z(y*)∉-cl(C)，知存在tz(y*)>0,使得

z(y*)-tz(y*)ε∉-cl(C(x*)),

再结合z(y*)-tz(y*)ε+intC(x*)为z(y*)的邻域，知

(F(x*,y*,λ)+ε)∩(z(y*)-tz(y*)ε+intC(x*))=∅,

注意到intC(x*)+intC(x*)=intC(x*)，由(A6)知，存在y*的邻域U(y*)，使得

(F(x*,u,λ)+ε)∩(z(y*)-tz(y*)ε+intC(x*))≠∅,∀u∈U(y*).

由y*∈K(λ)的任意性知，对每个y∈K(λ)，存在tz(y)>0及z(y)∈(F(x*,y,λ)+ε)∩(-cl(C(x*)))c,使得

z(y)-tz(y)ε+intC(x*)⊂(-cl(C(x*)))c,

以及存在y的邻域U(y)，使得

(F(x*,uy,λ)+ε)∩(z(y)-tz(y*)ε+intC(x*))≠∅,∀uy∈U(y).

再由K(Λ)为紧集，则对每个λ∈Λ，存在y1,y2,…,ym∈K(λ),使得

因此，对每个y∈K(λ),有

又对每个i∈{1,2,…,m}，z(yi)-tz(yi)ε∉(-cl(C(x*)))，则存在t1,t2,…,tm>0,使得

z(yi)-(tz(yi)+ti)ε∉(-cl(C(x*))),i=1,2,…,m.

令t=min(t1,t2,…,tm),则对每个y∈K(λ),有

注意到(1-t)ε+intC(x*)为ε的邻域，对每个δ∈intC(x*)，有

F(x*,y,λ)+(1-t)ε+δ⊄-cl(C(x*)),

故

V∩Φ1(λ,η)≠∅,∀η∈((1-t)ε+intC(x*)),

所以，Φ1(·,·)在Λ×Ω上下半连续.

定理2假设(A1)，(A3)～(A5),(A7),(A8)成立，则Φ2(·,·)在Λ×Ω上下半连续.

证明设(λ,ε)∈Λ×Ω，V为X中的开集，满足V∩Φ2(λ,ε)≠∅，x∈V∩Φ2(λ,ε).设x0∈V∩Φ2(λ,εμ),其中μ∈(0,1)，易知x0∈V∩Φ2(λ,ε).

现取x*∈V∩{xθ∈K(λ):xθ=θx+(1-θ)x0},由(A5)，有

(F(x*,y,λ)+ε)∩(-cl(C(x*)))=∅,∀y∈K(λ).

任取y∈K(λ)，对每个z∈F(x*,y,λ)，存在与z相关的tz>0,使得

z-(1-2tz)ε∉-cl(C(x*))，

再结合z-(1-tz)ε+intC(x*)为z+ε的邻域，知

再由(A8)知，存在z1,z2,…,zm∈F(x*,y,λ),使得

令ty=min(tz1,tz2,…,tzm),则

再由(A7)知，存在y的邻域V(y)，使得

故对每个u∈V(y)，有

(F(x*,u,λ)+(1-ty)ε)∩(-cl(C(x*)))=∅，

再据K(Λ)为紧集，则对每个λ∈Λ，存在V(y1),V(y2),…,V(ym),使得

记t=min(ty1,ty2,…,tym),则对每个y∈K(λ),有

(F(x*,y,λ)+(1-t)ε)∩(-cl(C(x*)))=∅，

则对任意的η∈((1-t)ε+intC(x*)),有x*∈Φ2(λ,η).故Φ2(·,·)在(λ,ε)∈Λ×Ω处下半连续，再由(λ,ε)的任意性，所以，Φ2(·,·)在Λ×Ω上下半连续.

3 上半连续性及连续性

在以下假设条件下，讨论Φ1(·,·)与Φ2(·,·)在Λ×Ω上的上半连续性.

(B1) 设X,Y,Z为实拓扑向量空间，M⊂X,Λ⊂Y为非空子集，C:M→2Z{∅}为具正真凸值的集值映射，D:M→2Z{∅}为C的交叉映射，K:Λ→2X{∅},F:M×M×Λ→2Z{∅}为给定集值映射；

(B2) 对每个(λ,ε)∈Λ×Ω，Φ1(λ,ε)≠∅；

(B3) 对每个(λ,ε)∈Λ×Ω，Φ2(λ,ε)≠∅；

(B4)K在Λ上具有紧值；

(B5)W:M→2Z{∅}为给定集值映射，W(x)=Z(-intC(x))具有闭图；

(B6) 对每个λ∈Λ,y∈K(λ)，F(·,y,λ)在K(Λ)上为D(x)-下半连续；

(B7) 对每个λ∈Λ,y∈K(λ)，F(·,y,λ)在K(Λ)上为D(x)-上半连续；

(B8) 对每个λ∈Λ,x,y∈K(λ)，F(x,y,·)在Λ上为D(x)-紧.

定理3假设(B1)，(B2)，(B4)，(B5)，(B7)，(B8)成立，则Φ1(·,·)在Λ×Ω上上半连续.

证明设(λ,ε)∈Λ×Ω，由K(λ)为X的紧集，则Φ1(λ,ε)有一个闭图.设网(λα,εα)→(λ,ε),xα∈Φ1(λα,εα)，由K(λ)为紧集，则必有xα→x∈Φ1(λ,ε).

事实上，若x∉Φ1(λ,ε)，则存在y∈K(λ)，使得

A(λ):=F(x,y,λ)+ε⊂-intC(x).

由(B5)知，对每个zλ∈A(λ)，存在zλ的邻域V1(zλ)及x的邻域V2(zλ)，使得

V1(zλ)⊂-intC(v),∀v∈V2(zλ).

设ezλ∈V1(zλ)∩(zλ+intD(x)),则ezλ-intD(x)为zλ的邻域，且

ezλ-intD(x)⊂-intC(v),∀v∈V2(zλ)，

据(B7)知，存在x的邻域U(x)，使得

F(u,y,λ)+ε⊂B(λ)-intD(x)=B(λ),∀u∈U(x).

F(u,y,λ)+ε*⊂B(λ)+tλθ-intD(x)=B(λ)+tλθ,∀u∈U(x),ε*∈U(ε).

F(u,y,λ)+ε*⊂-intC(u),∀u∈U(λ),ε*∈U(ε)，

这与(λα,εα)→(λ,ε),xα→x,xα∈Φ1(λα,εα)矛盾，故x∈Φ1(λ,ε)，所以Φ1(·,·)在(λ,ε)处上半连续.再由(λ,ε)的任意性，知Φ1(·,·)在Λ×Ω上上半连续.

定理4假设(B1)，(B3)～(B6)成立，则Φ2(·,·)在Λ×Ω上上半连续.

证明设(λ,ε)∈Λ×Ω，由K(λ)为X的紧集，则Φ2(λ,ε)有一个闭图.设(λα,εα)→(λ,ε),xα∈Φ2(λα,εα)，由K(λ)为紧集，则必有xα→x∈Φ2(λ,ε).

事实上，若x∉Φ2(λ,ε)，则存在y∈K(λ)及z∈Z，使得

z∈(F(x,y,λ)+ε)∩(-intC(x)),

故存在t>0,使得z+2tε∈-intC(x).由z+tε-intD(x)为z的邻域，结合(B6)知，存在x的邻域U1(x)，使得

(z+tε-intD(x)-intD(x))∩(F(u,y,λ)+ε)≠∅,∀u∈U1(x)，

又由D为C的交叉映射，则存在x的邻域U2(x)，使得

intD(x)⊂intC(u),∀u∈U2(x)，

再由W具有闭图，则存在x的邻域U3(x)，使得

z+2tε∈-intC(u),∀u∈U3(x).

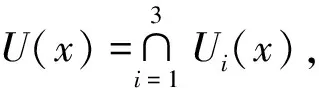
(F(u,y,λ)+ε*)∩(-intC(u))≠∅,

这与(λα,εα)→(λ,ε),xα→x,xα∈Φ2(λα,εα)矛盾，故x∈Φ2(λ,ε)，所以Φ2(·,·)在(λ,ε)处上半连续.再由(λ,ε)的任意性，知Φ2(·,·)在Λ×Ω上上半连续.

据定理1及定理3 知，(PGSVEP-1)的近似解Φ1(·,·)在Λ×Ω上具有连续性.

定理5假设(B1),(B2)，(A4)～(A6),(B5),(B7),(B8)成立，则Φ1(·,·)在Λ×Ω上连续.

据定理2,4知，(PGSVEP-2)的近似解Φ2(·,·)在Λ×Ω上具有连续性.

定理6假设(B1),(B3),(A4),(A5),(B5),(B6),(A7),(A8)成立，则Φ2(·,·)在Λ×Ω上连续.

4 结束语

在实拓扑向量空间中研究两类含参广义集值平衡问题，分别记为(PGSVEP-1)与(PGSVEP-2)，并给出(PGSVEP-1)和(PGSVEP-2)的近似有效解的概念.在适当条件下，分别给出了(PGSVEP-1)和(PGSVEP-2)的近似解映射Φ1(·,·)和Φ2(·,·)在Λ×Ω上的连续性最优条件.研究结果表明，两类含参广义集值平衡问题近似解映射的连续性理论具有统一性.