单叶函数若干子类的Hankel行列式H2(3)
王东荣,龙波涌,黄华鹰①
(安徽大学 数学科学学院,安徽 合肥230601)
0 引言
记C为复数集,N为自然数集,D={z∈C:|z|<1} 为单位圆盘. 记A为在单位圆盘D内解析,且满足正规化条件f(0)=f′(0)-1=0 的函数f(z)的全体. 则A中的函数有展开式

记S为A中单叶函数的全体. 分别记α阶星象函数、α阶凸函数以及导数的实部大于α的函数类为S*(α)、K(α)和R(α),则当函数f,g,h∈S且α∈[ )
0,1 时,有

显然,S*(0)=S、K(0)=K和R(0)=R分别是星象函数类、凸函数类以及导数具有正实部的函数类. 当α取特殊值时,对于所得到的函数类的研究也很有价值. 例如,令,则有,而函数类在解决一些微分方程问题中会常常碰到[2].
当f∈A时,Pommerenke[3-4]定义了函数f(z)的q阶Hankel行列式为

其中n,q∈N. 之后,Hankel行列式引起了数学工作者的极大兴趣.
当q=2,n=1 时,H2( )1 就是经典的Fekete-Szegö 泛函[5],早在1930 年就有人研究. 然而若将q或n的值取得更大,则对于Hankel 行列式的研究就会困难很多. 文献[6]首先研究函数类S*、K和R对应|H3(1 ) |的上界,后来有很多人研究H3(1 ) ,参见文献[7-10].
Janteng等[11-12]得到函数类S*、K以及R对应 |H2( 2 )|的最佳估计. Lee等[13]研究关于一个给定函数φ的Ma-Minda 星象函数类S*(φ)的二阶Hankel 行列式,并得到β阶的强星象函数类S*β的 |H2( 2 )|≤β2,α阶星象函数类S*(α)的 |H2( 2 )|≤(1-α)2. 其他一些函数类二阶Hankel行列式的研究见文献[14-17].

由式(2)有本文研究S*(α)、K(α)以及R(α)对应的二阶Hankel 行列式H2( )3 ,分别估计其对应 ||H2( )3 的上界.R(α)对应的 ||H2( )3 的上界是最佳的. 当系数a2=0 时,得到S*(α)和K(α)对应 ||H2( )3 的最佳上界.
1 预备知识
记P是由在D内解析且Re(p(z))>0,p(0)=1的全体函数. 若p∈P,则p有展开式

引理1[18]若p∈P,则p(z)展开式的系数有最佳不等式 |pn|≤2,其中n=1,2,….
引理2[19]若p∈P,则有最佳不等式 |pn-μpk pn-k|≤2,其中:μ∈[0,1] ;n,k=1,2,…;n >k.
引理3[20]若p∈P,则有,等式成立当且仅当以及它们的旋转.
注1 由文献[20]的证明过程可知,引理3 不等式中等号成立,当且仅当p2=0 或者 ||p2=2. 当
对于任意的f∈S*(α) ,有等式

其中:p∈P,α∈[ )
0,1 .
若f(z)与p(z)分别有表达式(1)与(4)且分别属于S*(α)和P,运用式(5)可以得到

则有
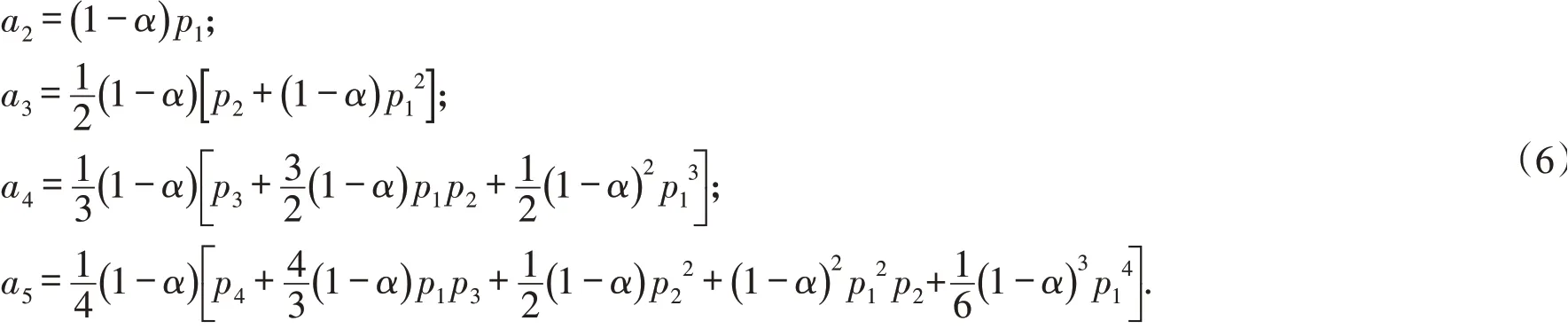
若f∈S*( )
α,则由式(3)与(6)有其中
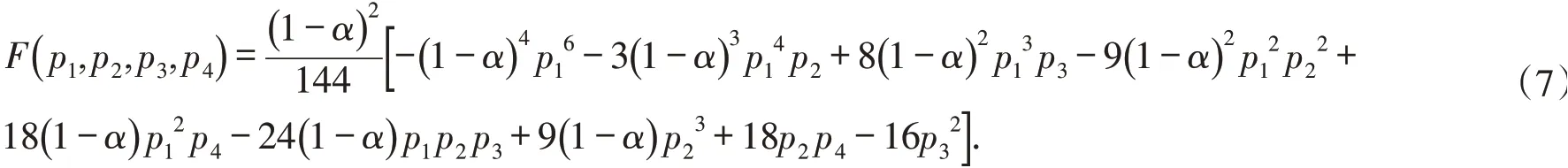
众所周知,f∈K当且仅当zf′(z)∈S*. 如果,则



2 主要结果
定理1 设,则
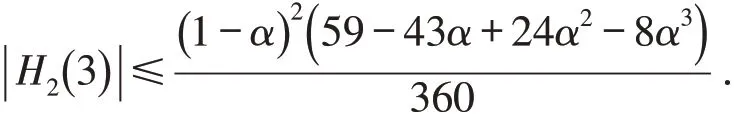
证明令,根据式(7)有
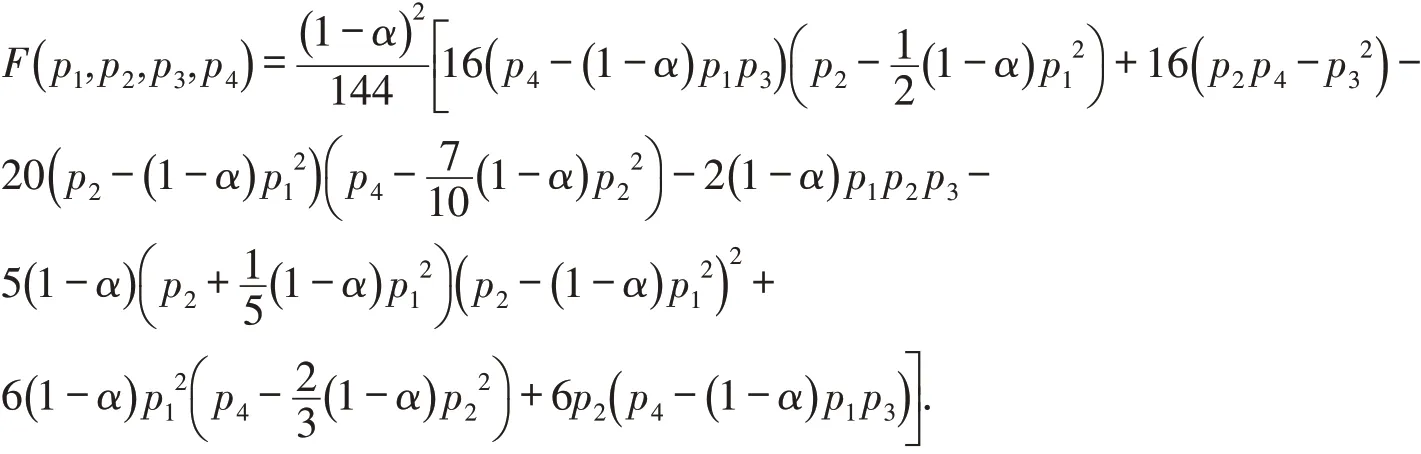
因为α∈( 0,1) ,从而1-α∈( 0,1) . 则由引理1~3有

如果f∈K(α),则根据式(9)有

由引理1~3可得

从而定理得证.
推论1 若,则;若,则
定理2 设α∈[ 0,1) ,f有展开式(1),且a2=0.
(1)若f∈S*(α),则
以上2个不等式均是最佳的.
证明因a2=0,则根据式(6)中第1个等式,可得p1=0. 若f∈S*( )α,则由式(7)可得
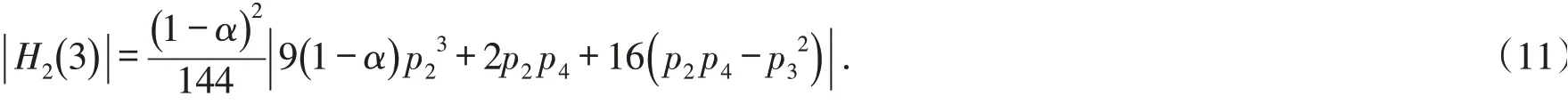
从而根据引理1和引理3有

若f∈K(α),根据式(9)可得

由引理1和引理3可得
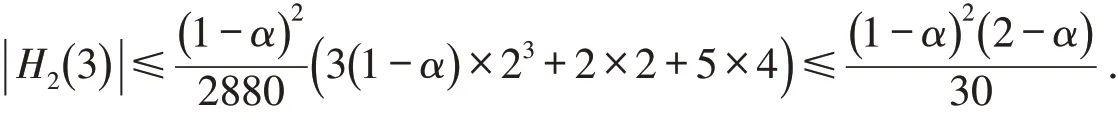
下面考虑定理2中的极值函数. 当f∈S*(α) ,综合引理1、3及式(11)知,式(12)中不等式等号成立当且仅当以及根据注1有,因此,若f∈S*(α),则极值函数
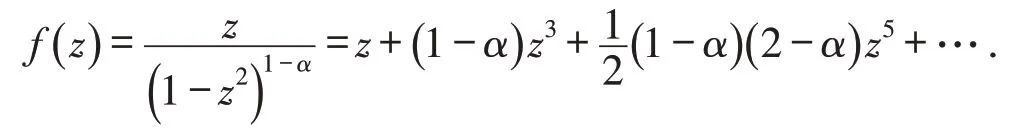

推论2 设f有展开式(1),且a2=0,
推论2中(1)和(2)的第2个结果在文献[20]中证明得到,显然结果是最佳的.
定理3 若f∈R(α),且,等号成立当且仅当

证明当时,根据式(10)有

由引理1和引理3可得
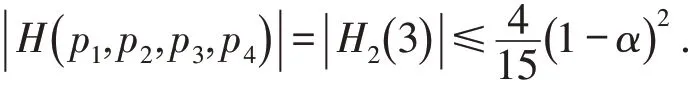
等号成立当且仅当 ||p2=||p4=2 以及,故根据引理3和注1可知从而可得极值函数
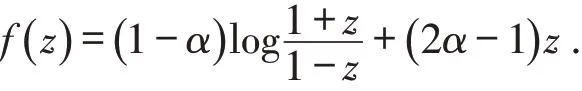
推论3 若f∈R,则;若
推论3当中的第1个结果在文献[20]中得到证明,结果是最佳的.

