股指期权推出效果的实证分析——以上证50ETF为例

邓 芹，侯为波①

（淮北师范大学 数学科学学院，安徽 淮北235000）

0 引言

随着金融领域的日益发展，金融衍生产品的作用也日益突出. 其中期权合约作为重要衍生产品之一，无论是在国际还是国内都表现出很活跃的发展状态. 借鉴国际市场期权交易的经验和制度保障，国内的期权交易市场正在快速发展，期权推出条件也已经基本成熟，但是还有很大的发展空间，期权合约的推出条件还需加强，创造更完善的期权交易市场.

期权是指其持有者在一个确定的时间按确定的价格买入或卖出标的资产的权利［1-2］. 期权可分为金融期权和商品期权［3］. 很多学者对期权进行研究得到相关结论. 王乐毅等［4］分析比较二叉树模型和Black-Sholes 模型（B-S 模型），得到两个模型在实质上是一致的结论；黄本尧［5］研究Black-Sholes 模型的精确性和适应性，得出尽管该模型的假设条件不能完全贴合实际但是依然是交易中不可或缺的分析工具；刘立刚等［6］将二叉树模型和Black-Sholes 模型结合在一起研究期权的时间价值和内在价值. 在已有的文献中大多是对期权的定价及模型选择进行分析，而本文主要利用上证50ETF期权数据并基于二叉树模型、Black-Sholes模型以及风险度量参数对股指期权推出后的效果进行分析. 从期货的市场功能、期权定价的合理性、期权各阶段的执行方式及风险度量几个方面综合分析，得出我国股指期权的推出效果良好，虽具有一定风险但是更有利于投资者进行规避风险. 这可以明确投资者的投资方向，选择合适的投资策略规避风险［7-8］.

1 模型建立

1.1 二叉树模型

二叉树模型是指利用二叉树图表示标的资产在有效期内可能遵循的路径［9］. 假设S0和f分别为股票当前价格和对应期权当前价格，当前时刻为零时刻，T为到期时间，股价可能的上升幅度为u（u ＞1），下降幅度为d（d ＜1），则对应的股票价格为S0u或S0d. 若价格上升到S0u，则对应的期权价格为fu，若价格下降到S0d，则对应的期权价格为fd. 相应的二叉树如图1所示.

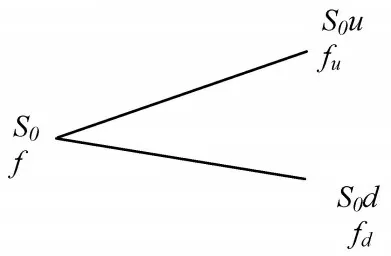
图1 单步二叉树模型

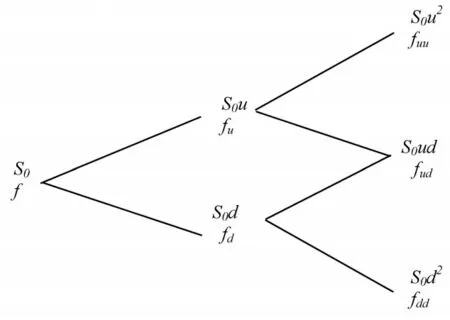
图2 2步二叉树模型

假设一个证券组合由Δ 股的股票多头和一个期权空头组成，在无风险的状态下，若股价上升则到期时组合价值为S0uΔ-fu，若股价下降则到期时组合价值为S0dΔ-fd. 二者的价值相等时有

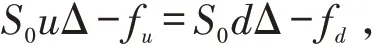
解得

设无风险利率为r，则组合价值的现值为，成本为S0Δ-f，则

进而得

其中

基于单步二叉树，当股价发生2次运动，每个时间长度为Δt，此时得到2步二叉树模型为

其中

fuu、fud、fdd分别为股票价格2次上涨、1次上涨1次下跌、2次下跌后对应的期权价格，相应的二叉树如图2所示.

1.2 Black-Sholes模型

Black-Sholes 模型假定很短时间内股票价格变化百分比服从正态分布［10-12］. 假设S0为股票当前价格，T为到期时间，σ为股票波动率，K为到期执行价格，c为看涨期权的价格，p为看跌期权的价格，r为无风险利率，则有不支付红利股票的看涨和看跌期权的Black-Sholes定价公式分别为

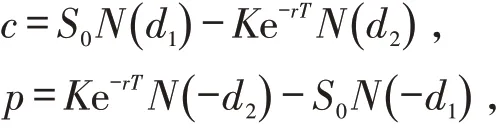
其中

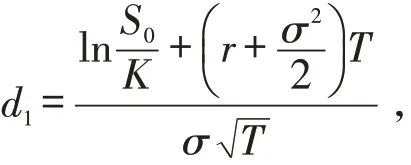
N(x) 是标准正态分布变量的累积概率分布函数.

1.3 期权的市场功能

期权的市场功能包括套期保值功能和价格发现功能［13］. 在市场功能的检验中套期保值比率是一个重要衡量指标，套期保值效果越好，期权市场功能越好. 期权的市场功能使得套利的手段和机会增加，有利于价格发现功能的发挥.

1.4 期权风险度量指标

Gamma是衡量Delta（期权价格变化对标的价格变化的比率）相对标的价格变化的敏感程度，期货和现货没有Gamma风险，只有期权有Gamma风险［14］. 基于不支付红利股票的看涨期权或看跌期权Gamma（Γ）值fΓ为

其中N′与前面的定义一样. 通过Gamma值来分析期权风险程度，Gamma的绝对值越小，风险越小.

2 实证分析

2.1 数据说明

本文选取的上证50ETF期权相关数据来源于东方财富网，数据范围是从2017年12月27日到2018年6月27日，现货价格选用标的收盘价，期货价格选用期货收盘价，利用SPSS19.0和Eviews7.0软件对数据进行处理.

2.2 市场功能检验

对上证50 股票的期、现货数据分别取对数得lnS和lnF2 个序列，再1 阶差分得ΔlnS和ΔlnF2 个序列.进行ADF值检验，如表1所示.

表1 平稳性检验结果

利用最小二乘法（OLS）模型对现货和期货数据进行回归求得线性方程式为

其他相应的数据，如表2所示.

表2 套保效果

从表1看出，期货、现货价格数据取对数后1阶差分序列平稳. 表2中得出OLS 模型的拟合度较高，套期保值比率较高，标准估计误差也很小，期货、现货价格之间的相关性也很好，说明期货市场的套期保值效果较好. 由期货和期权价格、现货和期权价格的相关系数得各市场之间有一定的关联性，为期权的推出创造良好的条件.

2.3 期权定价合理性检验

选取一个6 个月期的上证50 股票指数看涨期权，假设股票指数的当前价格为2.834，无风险利率为3.94%，价格波动率为21.75%，执行价格为3，利用二叉树模型为期权进行定价，结果如表3所示.

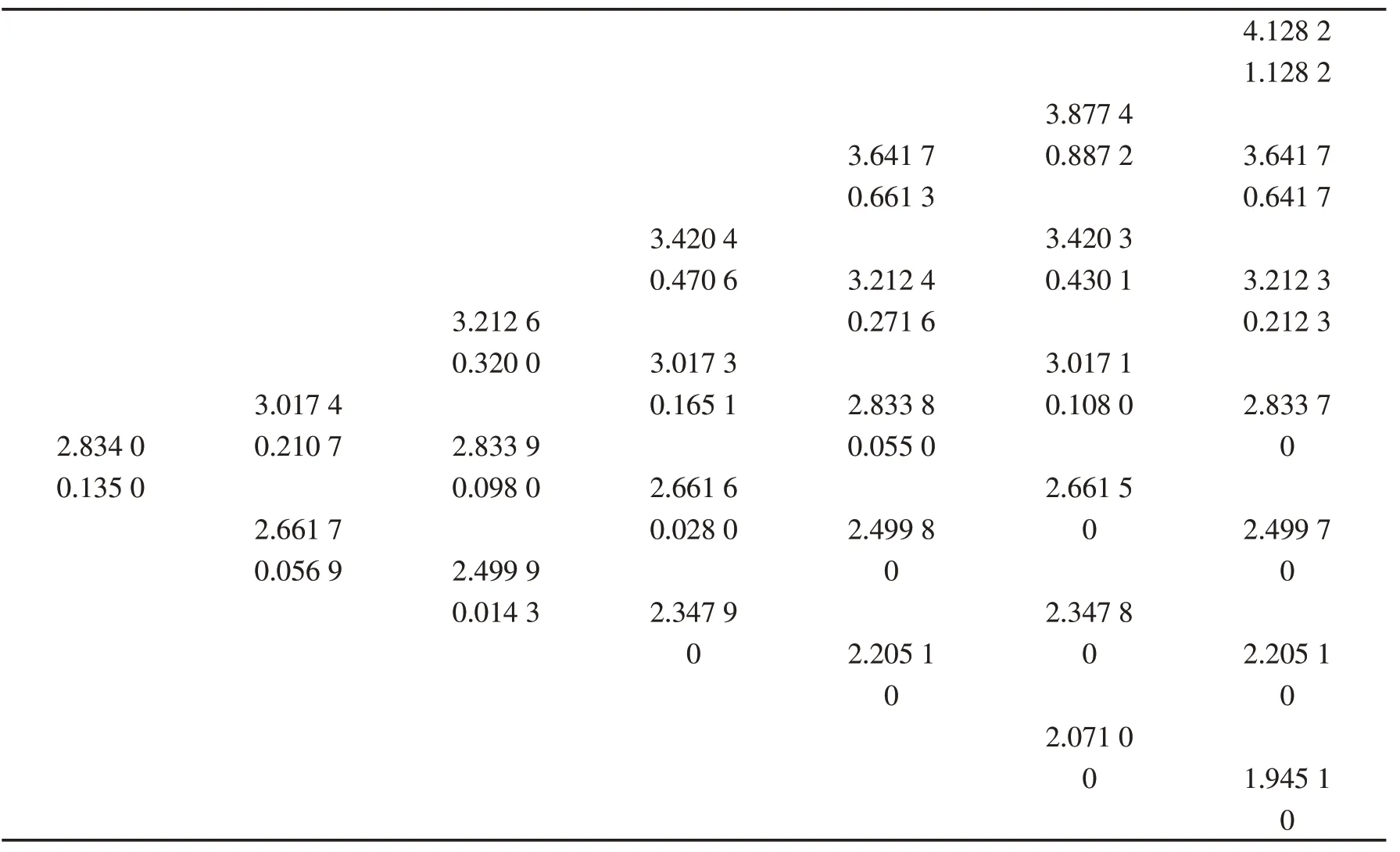
表3 二叉树模型定价

表3 是一个6 步二叉树模型求解出来的各阶段股票价格和期权价格，最后得出期权当前价格为0.135 0，与2017年12月27日的期权收盘价0.137 4误差相对较小，因此利用二叉树模型对期权进行定价是合理的.

利用Black-Sholes模型对不同期限的期权进行定价，能够看出期限的长短对期权定价的影响［15］.

表4 B-S模型各期限的定价

表4中的数据显示，随着期限的延长期权的价格最终趋近于0.124 1，这与2017年12月27日的期权收盘价0.137 4 相近. 说明期限足够长时，行使期权的机会就越多，期权价格越合理. 同时说明利用Black-Sholes模型对期权定价是合理的.

2.4 期权处理方式

通过对比二叉树图各节点的内在价值和时间价值来判断各节点的执行方式.

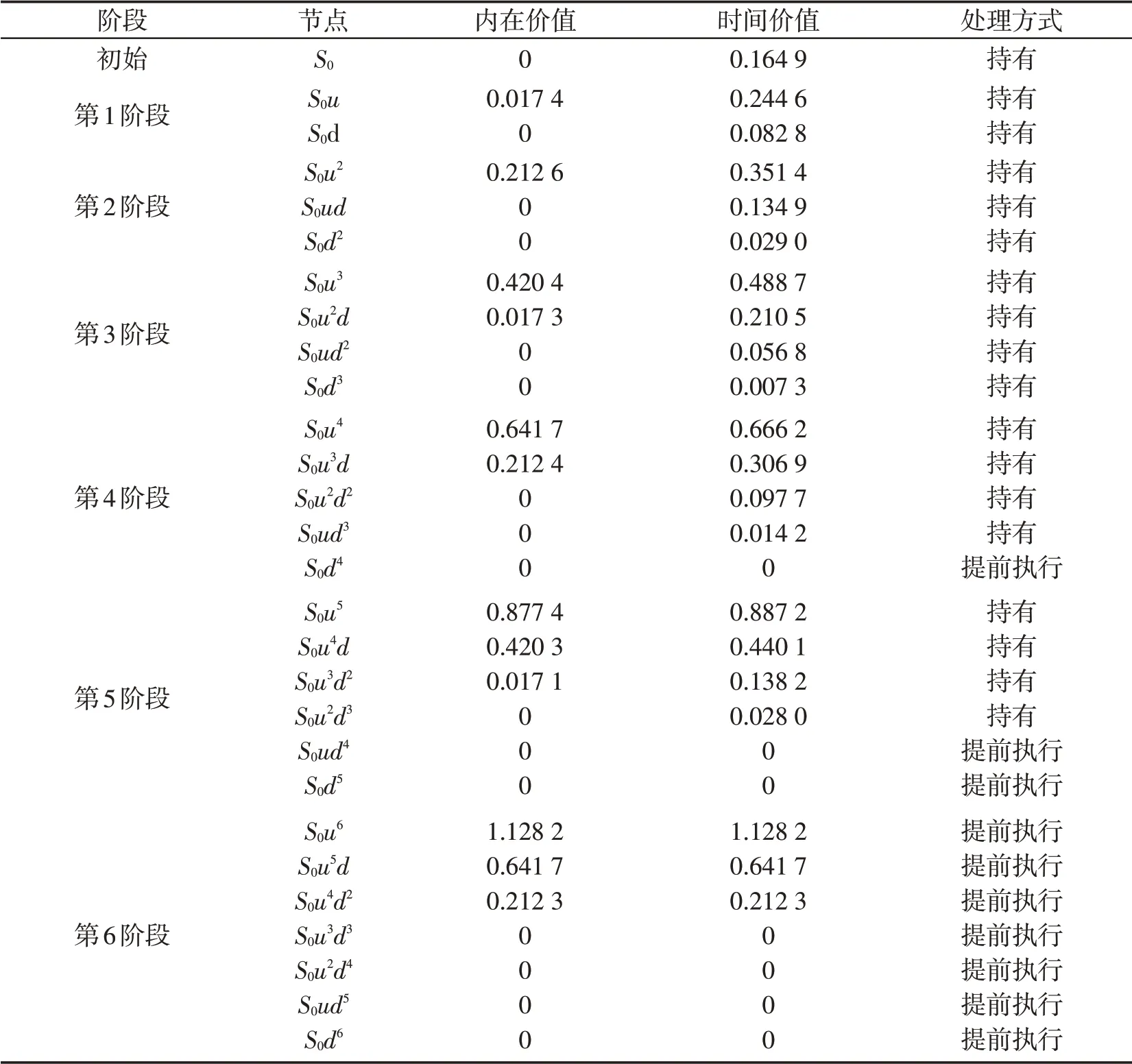
表5 各阶段期权执行方式

表5反映的是期权在各阶段的时间价值和内在价值. 通过对比各阶段中不同情况下的内在价值和时间价值来分析各种情况下期权的处理方式. 可以看出，越接近期权的到期日时间价值越小，时间价值大于内在价值应继续持有期权. 最后期权的时间价值等于内在价值应该提前执行，减小期权的执行风险.

2.5 期权风险度量

取一个6 个月期的上证50 股票指数看涨期权，假设股票指数的当前价格为2.834，无风险利率为3.94%，价格波动率为21.75%，执行价格为3，则股票期权的Gamma值为

说明该股票指数每增加或减少1个点，期权的delta值增加或减少约0.902 3.

3 结论

本文利用OLS模型、二叉树模型、Black-Sholes模型以及风险度量参数对股指期权的推出效果进行分析. 验证股指期权的市场功能良好，期权定价模型选择合理，投资风险在合理范围，为期权的推出奠定良好的基础，得出股指期权的推出效果较好，有利于投资者规避风险.

针对上面得到的结论给出相关建议. 利用期权合约进行保值时要综合考虑期权的市场功能，与期货市场结合起来制定期权推出策略，以保证其推出效果；股指期权的推出虽具有一定风险性，但是确实能够有效地控制股票市场的风险，投资者可以利用期权交易来减小现货市场的交易风险；期权交易中对期权进行定价时模型的选择要合理，得出一个合理的期权价格，在一定程度上更好地发挥期权的价格发现功能；作出合理的风险控制措施是必要的，选择好期权数量、期权交易的执行价格，明确期权各阶段的执行方式从而减小执行风险，总体考虑该期权推出后的利与弊再做出投资策略.