基于遗传算法的灌溉管网同步优化研究

侯依然, 上官林建, 侯泽林, 徐建新

(1.华北水利水电大学 机械学院,河南 郑州 450045; 2.华北水利水电大学 水利学院,河南 郑州 450046)

我国是农业大国,但落后的灌溉技术和粗放的灌溉方式使农业发展与水资源短缺之间的矛盾日益突出,无法满足可持续发展的要求。因此,必须大力发展节水灌溉技术,提高农业灌溉水利用率。管道输水灌溉作为提高农业灌溉水利用率的有效途径,具有蒸发量小、渗漏损失小和便于农田日常管理等优点[1],是发展节水型农业的必然趋势。针对灌溉管网进行合理的优化设计,对提高灌溉水利用率有显著效果。灌溉管网优化设计包括灌溉管网布置和管径优化两个方面[2]。其中,管网布置优化主要是指选择最优管线,使其实现总成本最小或总长度最短的目的[3-6]。最佳管径优化设计方案是在优化布置的基础上,通过水力计算来求得造价低的管径组合,其布置形式直接关系到管道总长度及工程合理性投资[7-10]。

前辈学者对管网优化设计常采用线性规划法[11]、非线性规划法[12]、动态规划法[13]等,随着近年来新型智能算法的不断发展,遗传算法[14]、人工神经网络[15]、粒子群算法[16]等被越来越多地应用于解决灌溉管网优化问题,促进了管道管网输水技术的推广与应用。由于常用的管网优化设计方法采用管网布置与管径分步优化来得到最优解,该解可能是局部最优解,而非全局最优解。为得到目标函数的全局最优解,本文运用遗传算法对灌溉管网布置与管径进行同步优化,以期为解决类似优化问题提供借鉴。

1 灌溉管道系统优化模型

以往学者在对农田灌溉管网进行优化设计时,大多以工程投资最低或年费用最低为目标函数建模；而近年来,很多灌区灌溉成本过高,给农民增加了负担,导致农民弃灌、水费征收困难等问题,严重制约了农业灌溉和灌区的运行和发展。因此,文中以灌溉管网供水成本最低为目标函数建立模型,进行管网的优化设计,选取最小的供水成本方案,降低农民的负担。

1.1 目标函数

本文以水泵的扬程、管网的管长和管径为变量,以灌溉供水成本最低为目标函数建立模型。其中,供水成本包括人工费、材料费(能耗费及水费)、施工机械使用费(固定资产费)、企业管理费等,即供水成本=(固定资产折旧费+运行成本费)/灌溉用水量[17]。

1.1.1 灌溉供水工程固定资产折旧费

灌溉供水工程固定资产的计算公式为:

(1)

式中:W为固定资产，元；W1为泵站工程的固定资产,元;W2为管网工程的固定资产,元;FP为泵站单位容量投资,元/kW;ρ为水的密度,kg/m3;g为水的重力,g=9.8 N/kg;Q泵为水泵流量,m3/s;H泵为水泵扬程,m;η装为水泵装机效率,无量纲;θ为管道附属费占材料费的比例;τ为人工费、施工机械使用费等占管材费的比例;Di为第i个管段的管径,mm;Li为第i个管段的长度,mm;a、b、c为与管道造价相关的比例系数。

固定资产折旧费的计算公式为:

(2)

式中:F为固定资产折旧费，元；K为设备的残余值(按固定资产的3%计)，元;r为设备的折旧年限,a。

1.1.2 灌溉供水运行成本费

灌溉供水运行成本费的计算公式为:

(3)

式中:G为灌溉供水运行成本费，元；k为运行成本系数;E为电费价格,元/(kW·h);m综净为综合净灌水定额,m3/hm2;S为灌溉面积,hm2;TZ为水泵年工作时间,h;η水为灌溉水利用系数;T为灌水周期,d;t为每日的灌水时长,h;e为水资源费价格,元/m3;m综毛为毛灌水定额,m3/hm2。

1.1.3 灌溉用水量

灌溉用水量Q的计算公式为:

Q=m综毛S。

(4)

1.1.4 目标函数

灌溉供水成本P的表达式为:

(5)

1.2 约束条件

管径约束为：

Di∈[D1,D2,…,Dn]。

(6)

式中n为选择的标准管径个数,i=1、2、…、n。

流速约束为：

vmin≤vi≤vmax,

(7)

式中vmax、vmin分别为管道允许的最大流速和最小流速,m/s。

节点压力约束为：

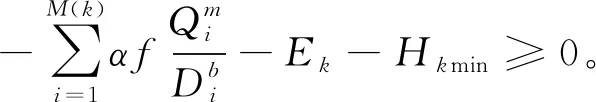
(8)

式中:Hi为第i个管段的水头，m;E0为水源水面标高,m;M(k)为从水源到节点k所经过的管段集合;α为局部水头损失系数,一般取1.1;f、m、b分别为与管材及水头损失有关的系数;Qi为第i个管段的流量;Ek为第k个节点的地面标高,m;Hkmin为第k个节点所要满足的最小水头,m。

管道承压约束为：

H0≤102HC。

(9)

式中:H0为管道首部的压力,MPa;HC为管道承受的最大压力,MPa。

高程约束为：

(10)

式中:Hs为吸上真空高度,m;Pa为大气压力,MPa;Ps为水泵进口处水流的压力,MPa;[Hs]为允许吸上真空高度,m。

流量连续性约束为：

A1V1=A2V2。

(11)

式中:A1、A2分别为管道变径前、后的截面面积,m2;V1、V2分别为A1、A2截面的流速,m3/s。

2 遗传算法的模型求解

2.1 遗传算法求解步骤

遗传算法是根据生物界的演变进化规律发展而来的一种搜索方法,因其具有很好的全局寻优能力,因此被广泛应用。其原理是从随机产生的初始种群出发,通过一代代不断进化,最终收敛到最适应的群体,从而求得问题的最优解。遗传算法的优化计算过程如图1所示，具体的求解步骤如下。

步骤1编码:对遗传算法的操作参数进行编码，依据编码规则给出种群的初始解。

步骤2适应度评价:建立与目标函数相关联的适应度函数,并计算个体的适应度值。

步骤3终止条件判断。

步骤4选择:从种群中选出适应度高的个体进行遗传。

步骤5交叉:将个体之间进行重组生成新的个体。

步骤6变异:将个体的基因位进行变异,产生新个体。

步骤7转到步骤3继续优化。

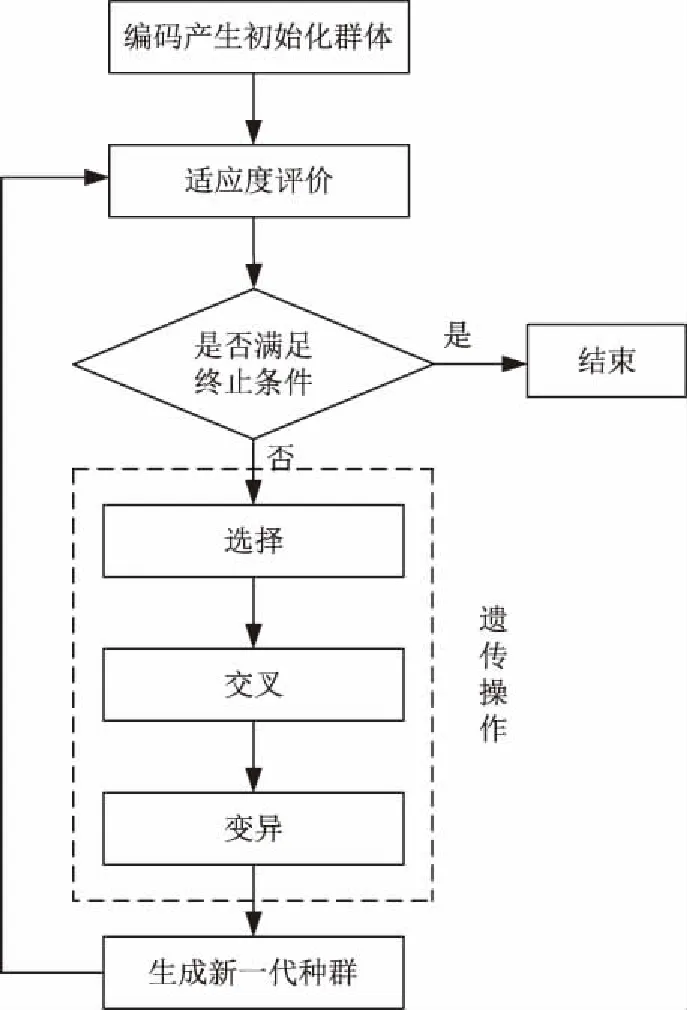
图1 遗传算法基本流程图

2.2 编码

对于树状管网优化,遗传算法是在符合约束条件的情况下,寻求运行成本最低的管网布置方案和管段管径组合，其所选个体必须能够对管网布置和管径组合进行完整的反映。由于这是一个对约束变量进行优化的问题,将管网布置与管径同步考虑,用遗传算法进行全局寻优,以每一个需水节点为基准,用整数方法编码。与二进制编码相比,整数编码可避免编码的冗余问题。编码的前半部分表示管网布置编码,编码的长度取决于需水节点的数目;后半部分表示管径组合编码。编码结构如图2所示。

图2 管网优化同步编码结构示意图

在树状灌溉管网中,根据图论算法理论,如果有N个需水节点,输水管段总数比需水节点数少1,即生成的树(管段)只有N-1条边,编码的长度与树的边数一致。以3.1节中的图3为例，管网中有10个供水节点,各个节点不存在角度约束问题,将下游的每个节点与上游有可能给它供水的节点相连,同时标出水流方向,然后对每一条连线按逆时针方向依次编号,染色体中的第2位基因就可以用{0,1,2}中的任意一个整数表示,其余节点的供水管段编码同理。如图3中,整数编码串[1,0,0,2,1,3,1,0,2]表示由管段[1][15][3][10][5][12][18][24][14]组成的生成树。

假设可供选择的标准规格的管径有5种,用0～4共5个整数依次对管径进行整数编码;假设可供选择的标准规格的管径有10种,用0～9共10个整数依次对管径进行整数编码;假设可供选择的标准规格的管径多于10种,用0～9加字母A—Z依次对管径进行整数编码。若此种管网的布置方案由10个管段组成,其中各个管段的管径分别为110、160、90、125、225、200、140、75、110、90 mm,则管径整数编码为[3,6,2,4,9,8,5,1,3,2]。

2.3 适应度函数设计

本文对约束条件的处理采用罚函数法。罚函数是指在求解最优化问题时,在原有目标函数中加上一个障碍函数,从而得到一个增广目标函数。罚函数的功能是对非可行点或企图穿越边界而逃离可行域的点赋予一个极大的值,即将有约束的最优化问题转化为无约束最优化问题。当搜索到可行域外的点时,合理的罚函数可使目标函数值变得很大,离约束条件越远惩罚越大。适应度函数y的计算公式为:

(12)

式中:λ1为流速惩罚因子,λ1=1/V=1/(ξVi);λ2为节点压力惩罚因子,λ2=1/H=1/(ξHi);λ3为管道承压惩罚因子,λ3=1/H=1/(ξH0);λ4为高程约束惩罚因子,λ4=1/H=1/(ξHs);ξ为惩罚因子系数,取0.9。

2.4 遗传算子选择

2.4.1 算子选择

采用轮盘赌选择法把个体的适应度与种群适应度的比值作为个体被选择的概率,据此来判断个体是否被选择并遗传到下一代。

2.4.2 算子交叉

将两个父代中的个体r1至r2之间的基因段进行两点交叉,交叉概率Pc=0.9。

2.4.3 算子变异

随机选择遗传个体和基因码位置,按照变异概率,改变其中一个或多个基因,使其在该位基因所允许的范围内随机变异。本文变异概率Pm=0.1。

2.5 终止条件判断

按照文中优化目标如果达到以下条件中的任何一个就可以终止计算：迭代次数超过预先设定次数；种群中遗传个体的最大适应度超过预先设定值。

3 实例计算

3.1 工程概况

对河南省某小型灌区的灌溉管网系统进行优化,结合灌区的地形、需水情况及管网连接经验等确定灌区管网的初步连接方式，如图3所示。其可能的管段有28条,水源点设为节点⓪。各管段对应长度见表1,各个节点的需水量及高程数据见表2,干管单价见表3,灌溉管道系统优化实例参数见表4。为防止管道被水锤现象及淤积破坏,管道内部允许水流速度最小为0.5 m/s,最大为3.0 m/s。采用勃拉休斯公式计算管道的沿程水头损失，局部水头损失按沿程水头损失的10%计；水资源费按照《河南省水资源费征收使用管理办法》中的标准收取。

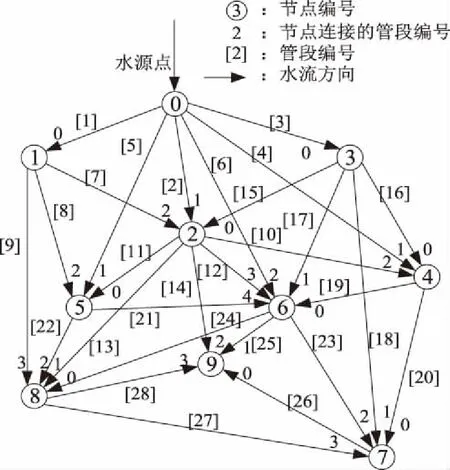
图3 管网初步连接图

表2 管网各节点数据

表3 干管单价

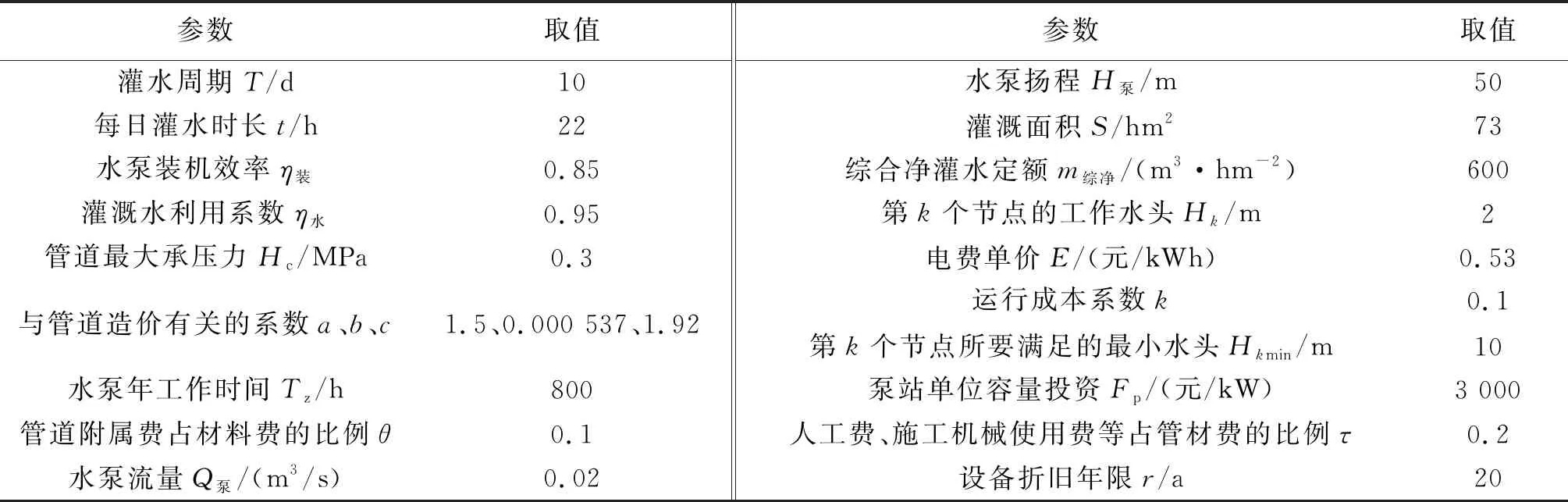
表4 灌溉管道系统优化实例参数表

3.2 管网优化

根据同步优化方案,采用遗传算法对问题进行优化,以达到全局最优的目的。利用 MATLAB R2016a进行编程求解,程序运行后，按照供水成本最小的原则得到5种优化方案。各方案的优化结果见表5，方案供水成本的变化曲线如图4所示。

表5 各优化方案比较

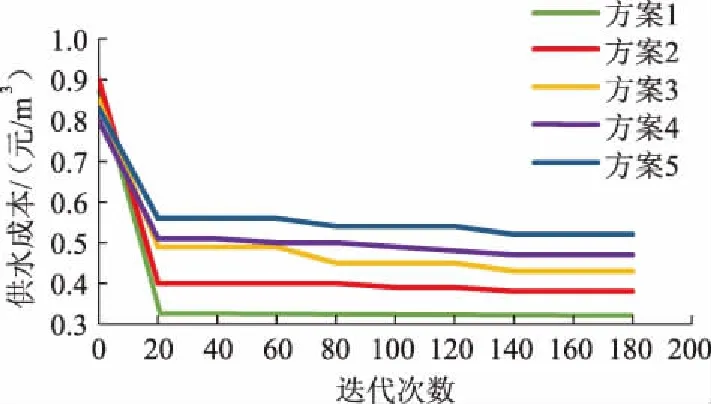
图4 5种管网优化方案的供水成本变化曲线

3.3 结果分析

工程原来的灌溉管网的优化方案(图5)是采用经济管径法,管网布置与管径优化是分步求解的，其管网总长为2 632 m,灌溉供水成本为0.470 0元/m3。本文运用遗传算法整数同步编码方式,建立了同步优化的供水成本模型,经MATLAB编程计算,以供水成本最低为原则得到优化的5种方案。经对比分析,文中方案2与原来管网布置方案的总长度相同,但灌溉供水成本为0.376 9元/m3,比原方案降低了19.8%,即方案2优于原方案。但是文中方案1的结果比方案2更优,方案1的管网布置形式如图6所示,其管网总长为 2 620 m,比原方案短9.4%;灌溉供水成本为0.320 9元/m3,比原方案的灌溉供水成本降低了31.72%。因此方案1为最优方案。

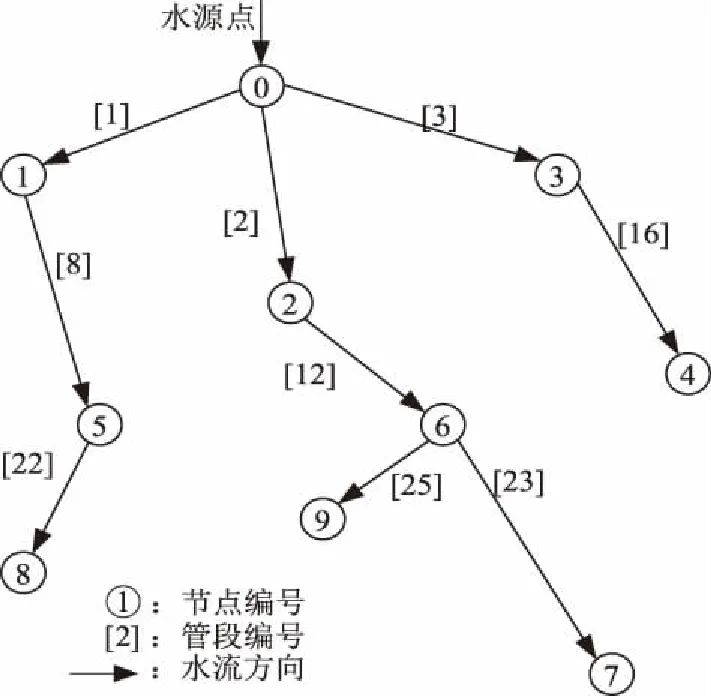
图5 原管网布置形式

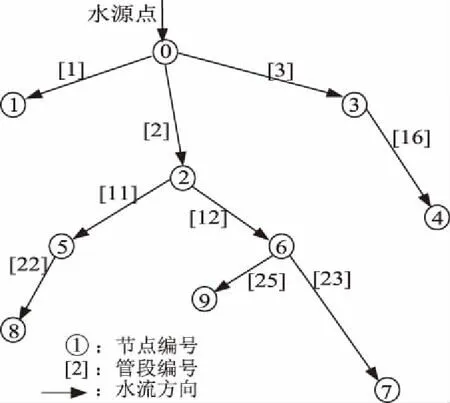
图6 最优管网布置形式

4 结语

本文以灌溉管网优化为例,建立了以灌溉供水成本最低为目标函数的灌溉管网优化非线性模型,运用遗传算法进行求解。在求解过程中,管网布置与管径优化采用整数同步编码方法,有效克服了二进制编码冗余的缺点和运算复杂性等问题。经过优化计算,得到5种优化方案，其中方案1的管网长度是几个方案中最短的,供水成本也是最低的。遗传算法成功克服了分步优化方法难以得到全局最优解的缺陷。该非线性模型在实际工程中的应用结果表明,灌溉供水成本明显降低,为农民进行农田灌溉提供了有利保障,为类似工程优化设计提供了参考和借鉴。