基于小波分解-Elman网络的灌区地下水埋深预测模型

张先起, 牛昂, 宋超

(1.华北水利水电大学 水利学院,河南 郑州 450046; 2.水资源高效利用与保障工程河南省协同创新中心,河南 郑州 450046)

地下水埋深是反映地下水资源量变化的重要指标。受开采、补给、蒸发等多种因素的影响,地下水埋深序列具有随机性、不确定性与非平稳性等特征[1],这为科学、准确地预测地下水埋深增加了一定的难度。目前,国内外学者对地下水埋深的预测研究主要基于回归分析、遗传算法、灰色理论与神经网络等理论。如:TAKAFUJI E H D M等[2]运用自回归积分滑动平均模型(Autoregressive Integrated Moving Average Model,ARIMA)的时间序列方法和序列高斯模拟(Symmetric Gauss Seidel,SGS)的地质统计方法预测了巴西包鲁地区地下水位变化;FIJAN E等[3]运用模糊逻辑模型对伊朗马拉盖·博纳卜地区地下水位进行了模拟;NADIRI A A等[4]利用遗传算法来选择隐藏层和节点的数量,优化了水位预测的深度神经网络(Deep Neural Network,DNN)模型;曹伟征等[5]针对地下水埋深预测精度不高的问题,提出了一种基于相空间重构(Phase Space Reconstruction,PSR)、粒子群算法(Particle Swarm Optimization,PSO)的极限学习机(Extreme Learning Machine,ELM)的非线性预测模型;吕萍等[6]利用灰色微分方程与自记忆原理构建了地下水埋深灰色自记忆预测模型,揭示了三江平原地下水埋深时间序列的变化规律。已有研究中,将单一神经网络应用于地下水埋深预测的[7-11]较多,而通过降低原始数据序列的非平稳性构建耦合模型的应用并不多见。本文基于小波分解在非平稳信号处理方面的突出表现及Elman神经网络对非线性与不确定性问题较强的自主适应性[12]等优点,构建了小波分解-Elman神经网络的耦合预测模型,并将其应用于人民胜利渠灌区地下水埋深预测中;为进一步验证模型的可靠性,将其结果与常用的BP神经网络模型和CEEMD-Elman模型的结果进行了对比。本研究以期为地下水埋深预测提供新的方法。

1 理论与方法

1.1 小波分解

小波分解就是利用小波基函数将原始信号分解成各个频率的子分量,然后分别重构子分量信号,以此获得和原信息尺度一致的多层信息的方法[13]。基于这一思想,地下水埋深时间序列可被分解成不同振幅和波长的若干个子分量,从而降低地下水埋深序列的非平稳性。

(1)

式中:a为收缩因子；b为平移因子；a、b∈R且a≠0。

对于任意函数f(t)∈L2(R),其连续小波变换可表示为:

Wf(a,b)=a-1/2ψ[(t-b)/a]。

(2)

其中,Wf(a,b)≤f(t)，

Mallat算法是Mallat在多分辨率分析的基础上提出的通过滤波器组实现信号的小波变换和反变换的一种算法。其原理为:将原始信号分解成不同频率的信号,得到低频部分与高频部分,然后将上次分解得到的低频信号再分解成低频和高频两部分,以此类推。Mallat算法如下:

(3)

(4)

式中:aj(f(k))、dj(f(k))是多尺度分析的离散逼近系数,分别代表低频分量和高频分量的小波系数;H(·)、G(·)为小波分解的滤波器,分别代表低通滤波器和高通滤器;f(k)为原始信号;j为分解层数,若分解的最高层为J,则j=J-1、J-2、…、2、1。

通过重构各层的小波系数,使序列恢复原有的长度,保证尺度的一致性。小波系数的重构公式如下:

(5)

式中,h(·)、g(·)是小波重构滤波器,分别代表低通滤波器和高通滤波器。

小波分解的实现步骤如图1所示。

图1 小波分解流程图

1.2 Elman 网络

Elman网络是一种应用较为广泛的动态递归神经网络。它基于BP神经网络结构[14],通过在隐含层中添加承接层来记忆隐含层单元前一时刻的输出值,使系统具有很强的适应性,进而实现快速寻优的目的[15-16]。Elman网络的结构如图2所示。

图2 Elman网络结构

图2中,u为r维输入向量;y为m维输出向量;xc为n维承接层输出向量;x为n维隐含层输出向量;W1为隐含层到承接层的连接权值;W2为输入层到隐含层的连接权值;W3为隐含层到输出层的连接权值。

Elman网络的表达式为:

x(k)=f(w2u(k-1)+w1xc(k));

(6)

xc(k)=a·xc(k-1)+x(k-1);

(7)

y(k)=g(w3x(k))。

(8)

式中:f(·)为隐含层神经元的激活函数;k为结构单元;g(·)为输出神经元的激活函数;a为反馈增益因子,0≤a<1。当a=0时,神经网络是标准的Elman网络;a≠0时,神经网络为修改后的Elman网络。

1.3 基于小波分解和Elman网络的耦合模型

基于小波分解原理,分解后的各频域分量对原始序列的贡献率各不相同。针对灌区地下水埋深序列,贡献率较大的分量在一定程度上决定了序列的变化,可以理解为是其变化的驱动因素[17]。因此,地下水埋深的预测可以分解为对其成分的预测。

小波分解与Elman网络预测模型的计算步骤为:

1)通过小波分解将地下水埋深原始序列分成高频分量和低频分量;

2)设置Elman网络参数建立网络,并利用训练数据对网络进行训练;

3)利用训练好的Elman网络对研究区地下水埋深序列的高、低频分量进行预测,并对其结果进行误差分析;

4)将预测年份的地下水埋深的高频分量和低频分量根据公式(5)进行累加,累加值与原始数据进行数据对比。

2 实例应用

2.1 研究区概况及数据来源

人民胜利渠灌区位于黄河中下游,是新中国成立后在黄河下游兴建的第一个自流灌区。灌区总控制面积为1 486 km2,多年平均降水量为620 mm,平均蒸发量为1 300 mm。地下水实测资料表明,近30年灌区内地下水位呈现下降趋势。

本文数据来源于人民胜利渠灌区地下水监测井1994—2012年的逐月实测数据,其变化曲线如图3所示。从图3中可以看出,1994—2012年人民胜利渠灌区的地下水埋深整体呈现上升趋势,并且各阶段的波动幅度不一致,这验证了地下水埋深具有不确定性和非平稳性。

图3 1994—2012年人民胜利渠灌区逐月地下水埋深变化曲线

2.2 小波分解

按照前述小波分解步骤对人民胜利渠灌区1994—2012年的地下水埋深序列进行小波分解。其中,分解层数根据杜文辽[18]提出的小波滤波分解层数的自适应方法确定。根据此方法,本文地下水埋深序列的小波分解最优层数为7,D1～D7为分解的高频序列,A7为低频序列;小波基函数根据小波基函数实验评价指标方法确定为db5。分解结果如图4所示。图4中纵轴D代表各高频分量,A代表低频分量。

图4 人民胜利渠灌区1994—2012年逐月地下水埋深小波分解图

从图4中可以看出：从D1到D7，各分量的频率逐渐减小,波长变短,波动性减弱;7个高频分量的数值均较小,而低频分量的数值较大。由此可见,低频分量对地下水埋深的影响最大,是其演变的主要驱动因素。

2.3 Elman网络建立及模型误差分析

以1994—2010年的逐月地下水埋深序列分解后的高、低频分量为训练样本,建立Elman网络模型,Elman网络模型参数设置如下:隐藏层神经元传递函数选择tansig函数,网络训练函数选择traingdx函数,输出层神经元传递函数为purelin。

将分解后的2011—2012年地下水埋深高、低频分量作为预测样本,利用建立好的模型对其进行预测,预测结果如图5所示,其误差分析结果见表1。

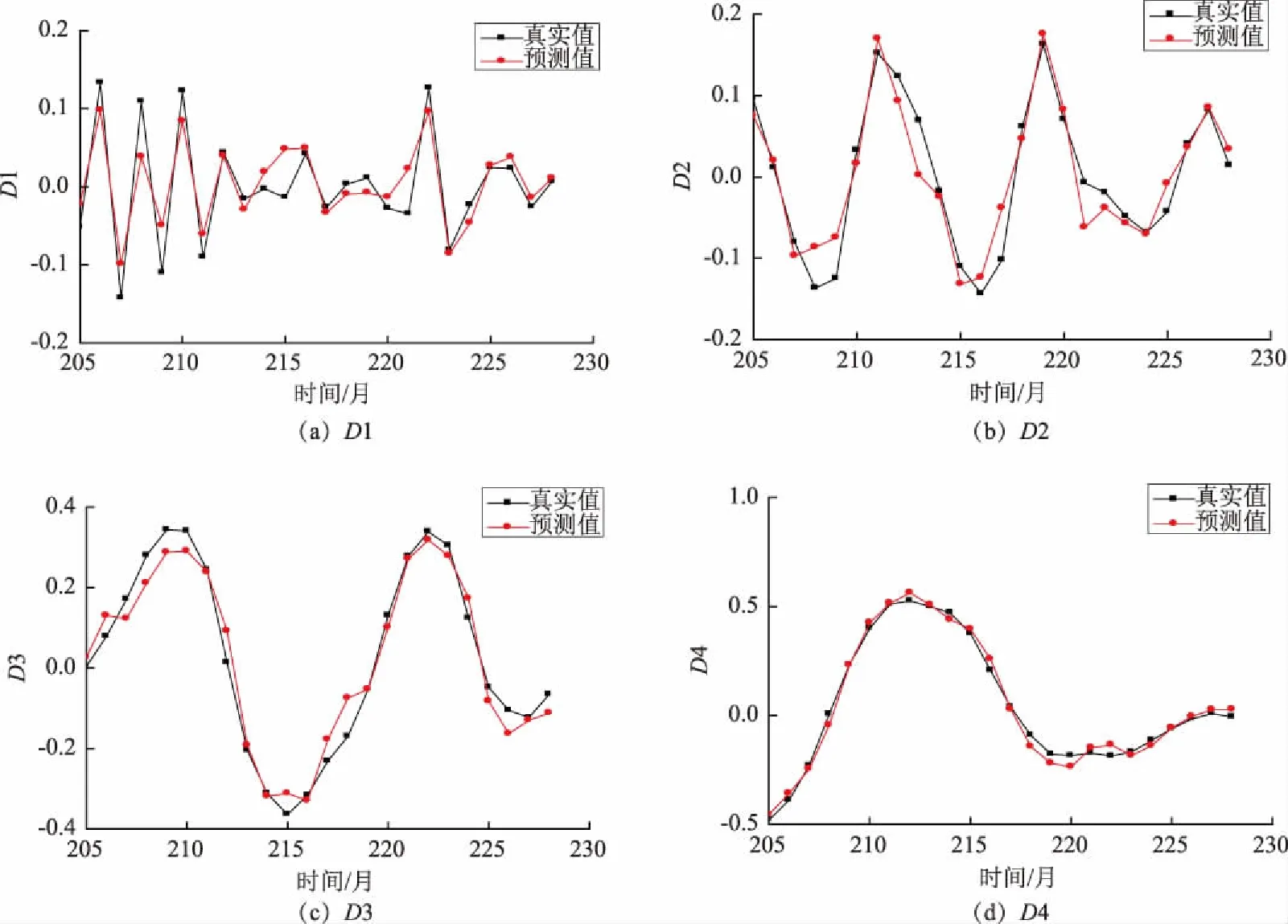
图5 2011—2012年地下水埋深高频分量与低频分量预测效果图

表1 地下水埋深高频分量与低频分量预测值与真实值之间的相对误差 %

由图5和表1可以看出:前4层高频分量的最大相对误差、最小相对误差、平均相对误差均较大;在高频分量中,D6的预测效果比较好;低频分量A7具有最佳的预测效果;尽管高频分量D1～D4的预测效果较差,但由于这些分量在地下水埋深序列中所占比例很小,因此对地下水埋深总误差的影响不大。

为了直观地看出模型的预测效果,利用小波系数重构公式计算出了2011—2012年逐月地下水埋深预测值,并将其与真实值进行了对比(图6),其预测误差见表2。

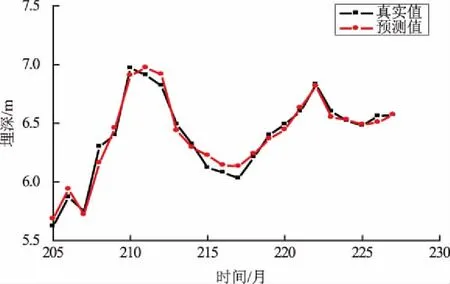
图6 2011—2012年地下水埋深预测效果图

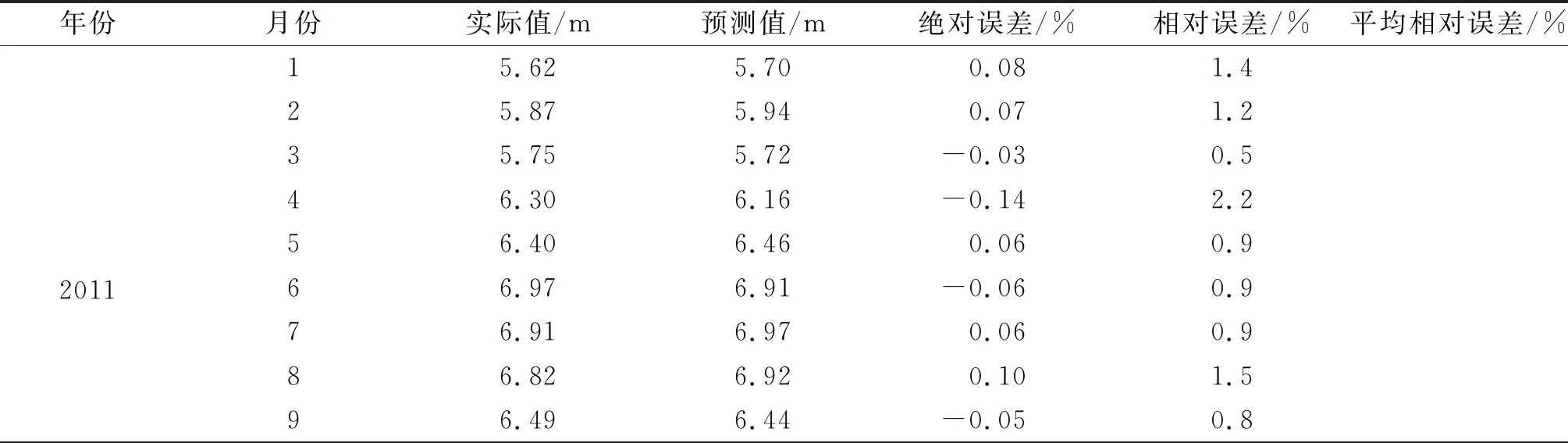
表2 2011—2012年人民胜利渠灌区的地下水埋深预测误差

续表

2.4 模型可靠性分析

为对比验证模型的精度,分别采用CEEMD-Elman模型和BP网络模型对2011—2012年的逐月地下水埋深序列进行预测,预测误差见表3，其对比情况如图7所示。

表3 小波分解-Elman模型与其他模型误差分析对比

图7 小波分解-Elman模型与其他模型的预测结果对比

通过与CEEMD-Elman模型和BP网络模型结果的对比可知，CEEMD-Elman模型预测的相对误差为8.1%,BP网络模型预测的相对误差为3.8%，而小波分解-Elman模型预测的相对误差为2.2%，说明小波分解-Elman模型预测地下水埋深的效果较好。

3 结语

本文将小波分解与Elman神经网络模型相结合,建立了小波分解-Elman神经网络模型,并将其应用于人民胜利渠灌区的地下水埋深预测中,为验证模型的可靠性,将其结果与常用的BP神经网络模型和CEEMD-Elman模型的结果进行了对比,得出以下几点结论:

1)构建的小波分解-Elman神经网络模型将地下水埋深序列进行分解、重构以后,从效果来看D1～D4高频分量的预测误差相对较大但占整体的预测比重较小;而D5～D7高频分量与A7低频分量的预测误差均较小,且在整体预测中所占的比重较大,所以预测模型的精度是可靠的。

2)将构建的小波分解-Elman耦合模型应用到地下水埋深预测中,整体预测效果较好,相对误差以及绝对误差均较小。

3)将CEEMD-Elman模型、BP网络模型预测的地下水埋深结果与小波分解-Elman模型的预测结果进行对比,CEEMD-Elman模型预测的相对误差为8.1%,BP网络模型预测的相对误差为3.8%,而小波分解-Elman模型预测的相对误差为2.2%,说明小波分解-Elman模型能较好地预测地下水埋深。