不同来流条件及沙波形态对沙波湍流场的影响
李锦鹏, 朱良生
(华南理工大学,广东 广州 510000)
沙波常出现于河口海岸地区,是水流与泥沙颗粒集体运动共同作用下的产物,其形成的沙波地形在冲积河流的河口区域尤为明显,在海岸带的浅水区域也常常能观察到这种特殊的地形。泥沙运动、床面阻力以及边界层发展等问题都与沙波的研究密不可分,作为河床阻力的重要组成部分,其具有周期变化的波状表面对于近底流动有着极大的影响[1-2],即使是在波幅不大的情况下,沙波也会引起表面边界层的脱离和涡旋的猝发,进而影响上部水流的湍流结构。在这个过程中,水流不仅受到沙波地形的影响,同时也受到来流条件的制约,因此,研究不同来流条件以及沙波形态对水流结构的影响有重要的意义。
已有许多学者对沙波的湍流结构进行了大量研究。ENGEL P等[3]通过对比不同沙波试验发现,只有在平坦床面时流动阻力才会受床面粗糙度的直接影响,当床面存在一定的起伏时,流动阻力便转由形状阻力主导,对沙粒阻力则不再敏感。LYN D A[4]通过概化的三角沙波模型,分别测量了对称的锯齿状床面和非对称的沙波床面两种形态下的水流湍动特征,发现床面形态的影响体现在尾流系数的变化中,在远离床面一定距离后,湍流特征趋近与平坦床面相一致。白玉川等[5]通过在大型水槽中模拟自然生成的沙纹,利用声学多普勒测速仪(Acoustic Doppler Velocimetry,ADV)监控沙纹床面不同位置处的流速过程,得到了水流的精细湍流结构。马殿光等[6]通过小水深沙波水槽试验,在假定存在次生流的基础上,对沙波沿程以及垂向的流速分布进行了测量,得到了适用于沙波迎流面的流速垂线分布公式。KIRKIL G[7]则是利用分离涡算法(Dettached Eddy Simulation,DES)模拟了二维沙丘上的两个平行流之间形成的浅混合层,研究了混合层结构在纵向上的非均匀结构及其演变过程。BRISTOW N等[8]通过粒子图像测速仪(Particle Image Velocimetry,PIV)对新月型沙波模型上的湍流场进行了详细测量,并以解耦的方式研究了沙波湍流的流场结构;ZHENG Yan等[9]利用PIV测速仪测量了沙波后的三维尾流结构,通过小波分析揭示了沙波尾流中的多尺度结构以及相关统计量的变化,并指出大尺度结构主导了沙波尾流的产生,且尾流与主流的相互作用会引起二次涡动。上述对沙波问题研究的侧重点主要在沙波的形成机理、过程以及沙波湍流的特点,而对沙波本身的形态和不同来流对沙波流场的影响方面的研究则相对较少,不同的沙波形态和水流条件的改变对湍流场造成的影响仍然不清楚。鉴于此,本文基于FLEMMING B W[10]的沙波形态统计规律和文献[4]中的物理模型试验结果,利用数值模拟的方法研究不同来流条件以及沙波形态对沙波上覆湍流场的影响,探讨沙波湍流的水流结构,以及不同雷诺数与沙波形态对湍流结构的影响。
1 沙波模型概化
1.1 理论方程
沙波湍流为不可压流,一般认为其流体的密度为常数。建立其数值模型时,考虑流域内的任一网格单元作为研究对象,流体在运动过程中遵循质量守恒定理与动量守恒定理,其控制方程分别为:

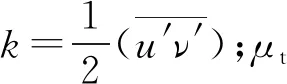
1.2 模型选取
应用较为广泛的k-ε双方程模型在沙波湍流场的模拟上有着一定的局限性[11]。原因在于k-ε模型假设流动为完全湍流,仅适用于远离壁面的流动完全发展区域,对于边界层内以黏性力为主导的层流流动,则是利用了一组半经验的壁面函数去描述,无法准确描绘边界层内部的变化情况。对于沙波湍流而言,当水流流经波峰后,会形成较为复杂的边界层分离和背水面回流现象,回流区内存在较大的逆压梯度[12],湍动的程度也明显增大,此时,再用壁面函数去描述该区域的流动显然是不合理的。
基于上述原因,本次模拟选用改进的SSTk-ω模型[13],通过在方程中引入阻尼因子和比耗散率ω,进而计算流域内的湍动黏度,对于远离壁面的湍流发展完全区域仍可以利用k-ε双方程进行求解,而在近壁面区域由于雷诺数较低,湍动黏度相比于动力黏度较小,可以对边界层内的流动进行直接求解。
模型计算湍动能k和比耗散率ω的方程分别为:
式中:k为湍动能;ω为湍流比耗散率;Γk和Γω分别为k和ω的有效扩散系数;Gk和Gω分别为由时均流速梯度引起的湍动能项和耗散项;Yk和Yω分别为由湍动引起的k和ω的耗散项;Sk和Sω则是关于k与ω的源项。
模型中流动的湍动黏度μt为:
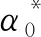
1.3 自由表面处理
要使得模型能最大程度地反映实际状态下的流动,就必须考虑自由表面的问题。自由表面本质上是2种不同流体介质的交界面,在自由表面的两侧,流体介质的物理性质不同是其最为特殊的性质,也是导致其求解不易的根本原因,两侧流体的特征物理量如密度、黏滞性、比热容等的不同为自由表面的计算带来很大的困难。
对于自由表面计算困难的问题,目前应用较为广泛的解决方法有刚盖假定法、流体体积(Volume of Fluid,VOF)法[14]、CLSVOF法[15]等。对于沙波湍流而言,当水深较小时,沙波床面对上覆流动的影响可以延伸至自由表面位置,造成自由表面的起伏和波动。
本文选用VOF法计算自由水面的位置,其基本思想是,在欧拉网格中定义一体积分数函数f,要求各相在一个计算单元中的体积分数总和为1,并通过求解连续方程和动量方程模拟各相流体的运动,追踪得到每个单元中各流体的体积分数,以某个体积分数区间内的单元群的坐标来确定自由液面的位置。
以气液二相流为例,如定义fwi(x,y,z,t)为i单元中液体的体积分数,则气体的体积分数fai(x,y,z,t)为:
fai(x,y,z,t)=1-fwi(x,y,z,t)。
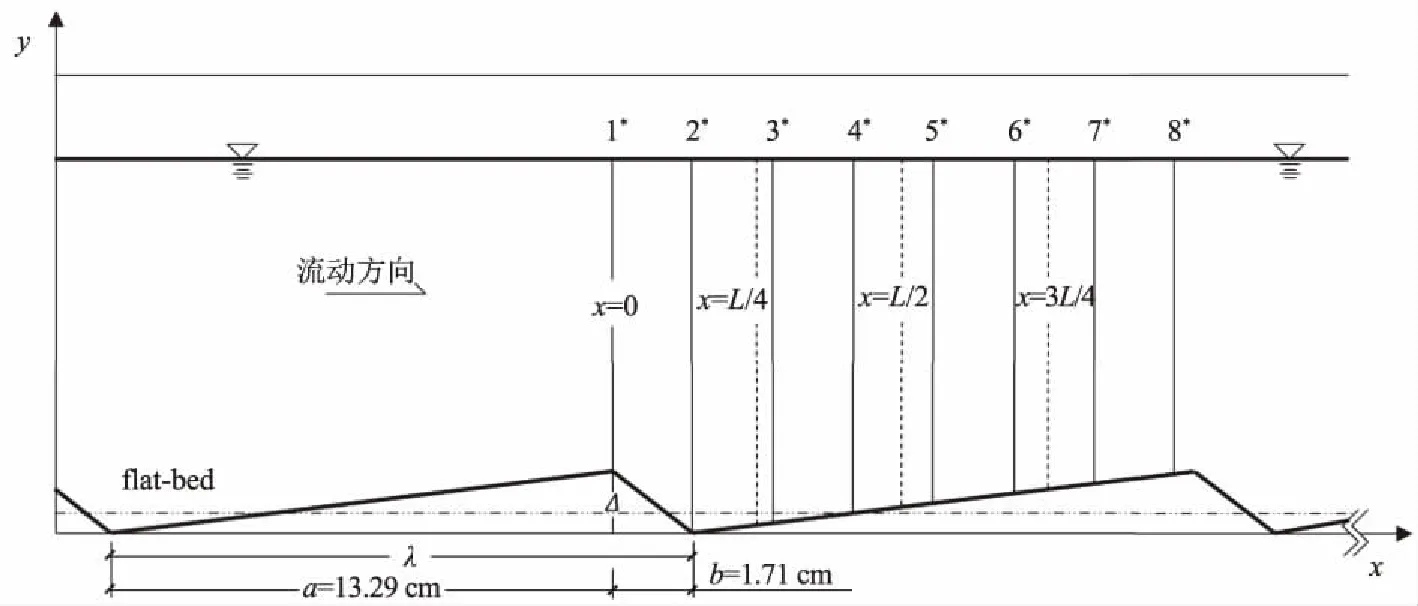
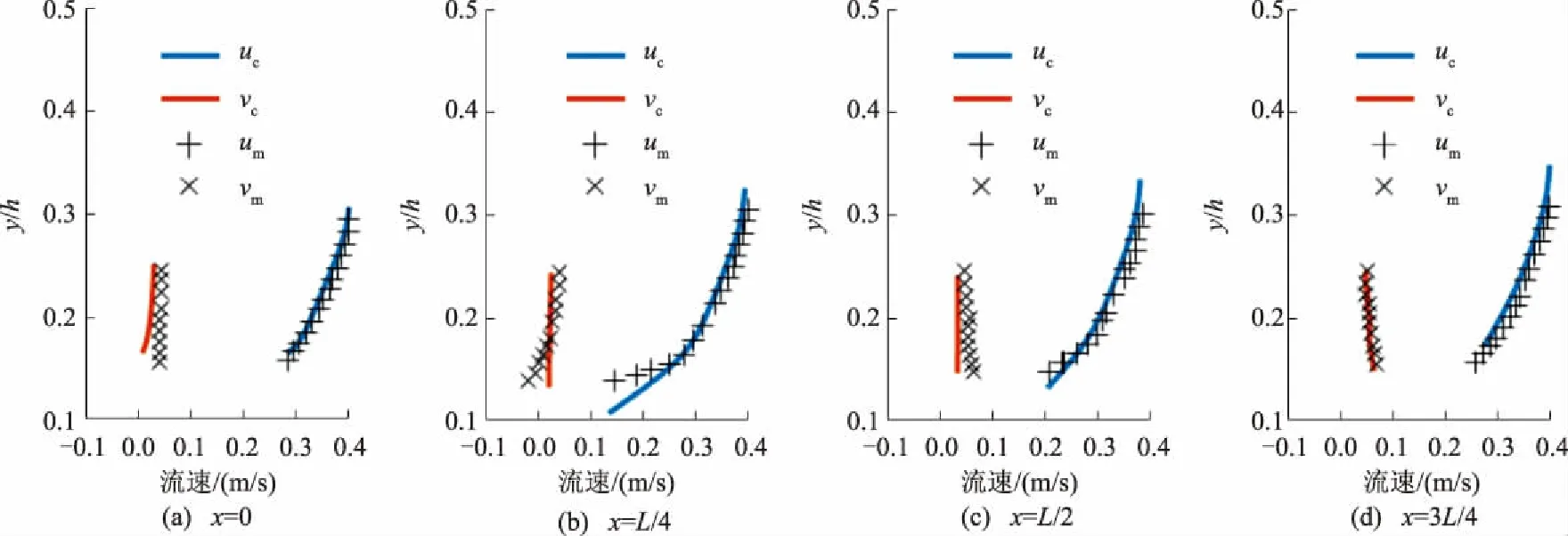
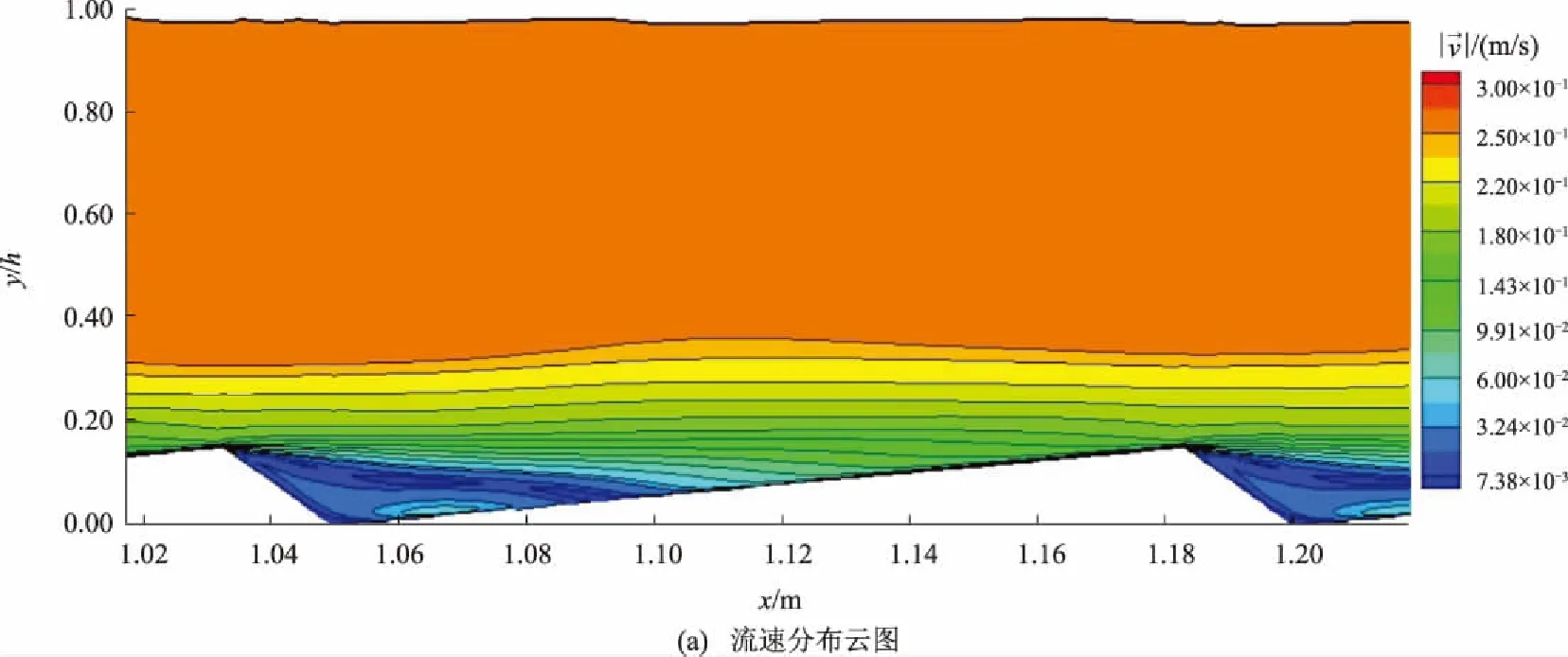
若fwi=1,则表示i单元内充满该液体;若fwi=0,则表示i单元内为没有该液体或者说充满了另一相的气体;若0 当自由液面发生变化时,以液相为例,通过体积分数的控制方程 可求得变化过后的体积分数的值。 当所有的这些单元位置都能被确定时,自由液面的位置和形态也就自然而然地确定了。 基于Fluent软件建立了二维数值水槽,流域总长200 cm、高10 cm、水深8 cm,水面以上为空气。概化后的沙波波长为15 cm,背流面与迎流面的水平距离之比a/b=0.129,沙波依次从距离进口60 cm的位置开始布置,保证流动在接触到第1个沙波之前充分发展。此外,上游位置的沙波对上部水流的影响有可能传递到下一个沙波区域,因此,选择第3个沙波设置测量断面,以保证这种影响不会被忽略。各测量断面如图1所示。 此外,在选取不同波陡的沙波床面作为研究对象时,要考虑到自然条件下沙波的波高与波长之间存在着一定的相关关系。根据FLEMMING B W[10]对全世界1 491个包含河口地区及海岸浅水区域的沙波地形进行统计分析的研究成果,得知沙波的平均波高Hmean、最大波高Hmax与波长L的关系式分别为: Hmean=0.067 7L0.809 8, Hmax=0.16L0.84。 以其研究成果作为参考,选取合适的波陡进行建模。 流域采用四边形网格进行剖分,平均网格尺寸为1 mm,为获得边界层内的流动结构还需要对近壁面处的网格进行加密,第一层网格的中心到壁面高度为0.1 mm,网格增率为1.05,以保证近壁面第一层网格的中心到壁面的无量纲距离y+≈1,最终流域的网格总数在30万个左右。 图1 概化后的沙波模型示意图 为了检验该模型的可靠性,采用学者LYN D A[4]的试验数据对该模型进行验证,分析数值模拟的结果与物理试验结果之间的差异大小。在对非对称沙波床面的试验当中,其来流流速为26.9 cm/s,雷诺数Re和弗汝德数Fr分别为16 400和0.35,各测量断面的位置为从波峰开始往后0、L/4、L/2、3L/4(L为波长)处(图1虚线位置),试验测量水深范围为1.2~2.4 cm,对比结果如图2所示。图中:u和v分别为水平流速和垂向流速;下标m、c分别表示试验值与模型计算值;纵轴y/h为各网格单元的纵坐标y和水深h的比值。 图2 各断面的流速分布对比 由图2可以看出,对于垂向上的流速,计算值与试验值在数值上相近,但分布趋势略有差别,原因在于双方程湍流模型假设流动是各向同性的。因此,模型中垂向各流层之间的黏滞力要略大于实际值,当垂向的流速较低时这种效应较为明显。对于水平方向的流速,模型的计算值与试验值两者之间差异较小,垂线流速分布趋势也与试验的一致。 为了定量地说明模型计算结果与物理试验之间的吻合程度,定义吻合度P作为评价的指标, 式中:P为吻合度指标;uim和uic分别为试验中第i个测点水平流速的试验值与计算值。容易看出,当试验值与计算值之间的差异越小,吻合度的值会越大。 由图2可以看到:4个测量断面中,吻合度最好的位置在波峰处,为0.978;吻合度最低的位置在回流区的影响区域,为0.913。考虑到回流区局部的流场更为复杂,因此在该处的吻合度会相对低一些。即便如此,各个断面试验值和计算值的吻合度都超过了0.9,认为该模型总体上能够较好地反映实际。 为准确描述流场的整体分布特征,在一个沙波长度范围内选取8个测量断面(1*、2*、…、8*),布置如图1所示,不同工况下的模型参数见表1。其中工况1、工况3、工况4为一组,观察雷诺数改变带来的影响;工况2、工况3、工况5为一组,改变沙波的波高,以观察沙波形态对流场的影响;flat-bed为床面沙量相同时平坦地形的工况,床面位置正好在沙波高度的1/2处,如图1所示。 表1 各工况的模型参数 以工况3为例分析沙波影响下的水流结构。由于沙波地形的存在使得床面阻力大大增加,上游来流行至迎流面时受其阻挡,造成近底流速下降而上部流速升高,流速降低的同时动能转换为压能,近底面水流的压强增大使得该区域很快出现了较高的壅水,在沙波位置处的水位变化过程如图3所示。从图3中可以看出:在很短的时间内,从上游往下水深很快上升至0.094 m;随着流动持续进行,一方面,越过波峰的边界层发生分离并破碎,产生大量涡旋;另一方面,背流面的回流区初步生成,水流在该处发生强烈紊动使得能量大量耗散,水位开始逐渐下降。水深减小过程中,过流断面面积也在不断减小,流量不变情况下流速增大,沙波对水流的阻挡作用也愈发强烈。当水深减小至0.07 m时,水面开始再次壅高。当流动进行至12 s时,内部流场逐渐稳定成为定常流,水深也维持在0.08 m不变。整个流动自由面的起伏变化过程也是水流内部结构在不断调整的表征。最终,水面不再变化意味着内部结构的分布已经趋于稳定。 图3 沙波位置处水位随时间的变化过程 沙波湍流各断面的垂向流速分布如图4所示,图中U为断面平均流速。由图4可知,在平坦床面处,水平流速随水深的增加而减小,在垂向上呈对数分布。而当沙波地形存在起伏时,受地形影响,水流沿程的流速分布在不断调整,迎流面的高度逐渐抬升对水流产生了加速作用,再加上过流断面面积的减小使得上部流速比平坦床面时的略有增大。在相对水深y/h>0.35时,水流流速保持在26.5 cm/s左右;相对水深y/h<0.35 时为边界层影响范围,受黏滞力作用的影响,水流在垂向上存在较大的流速梯度,近底流速相较于平坦床面有所减小。 图4 沙波湍流各断面的垂向流速分布 沙波床面对水流起到了阻挡的作用,背流面一侧的流速大大降低,垂向的流速分布发生改变,并在背水面一侧形成回流。根据能量守恒定理,流速降低的同时动水压强增大,边界层受回流区的推挤作用向上抬升,使得流动在越过沙波波峰后发生明显的边界层分离现象,当流动稳定后,回流区内的流速分布如图5所示。 图5 回流区内的流速分布 沙波湍流的湍动能分布如图6所示。从图6可以看出,水流湍动最为强烈的地方正好是边界层与回流区交界处,也是垂向流速的梯度达到最大的位置。边界层脱离床面后紧贴回流区向下游移动,回流区上部流层在黏滞力作用下流速逐渐增大,对边界层的顶托作用也沿程降低,至某一位置处边界层重新附着于壁面。近底面水平流速为零的位置为边界层的再附着点,从流动分离发生的位置至再附着点的水平距离称之为回流区的长度lr[16]。通过观察可以得出,背流面回流区的长度与沙波波高的比值为lr/h=5.17,与文献[17]中通过物理试验得到的统计均值lr/h≈5.2十分接近。 图6 沙波湍流的湍动能分布(工况3) 沙波湍流的涡量场如图7所示。分析沙波湍流的涡量场,观察图7(b)可以看到,水流越过沙波波峰后拐角处的涡量Ω达到最大,原因是边界层发生分离后其厚度迅速增加,进入主流后边界层内外区强烈的相互作用导致涡旋的猝发。涡旋会以周期性脱落的形式,对两侧流动进行强烈的扰动[18],在涡旋随流动向下游运动的过程中动量急剧耗散,在这个过程中大尺度涡旋逐渐向小尺度涡旋转变,小尺度的涡旋向下游和两侧流层扩散形成涡旋尾迹。由图7可以看到,涡旋尾迹由回流区与边界层的交界区域向两侧扩散。 图7 沙波湍流的涡量场 结合工况1和工况4,分析雷诺数发生改变后涡量场的变化。由图7(a)和图7(c)可以看到,波峰处的涡量随着来流雷诺数的增加而增大,高雷诺数下的涡流尾迹相比低雷诺数时范围更大,向下游扩散也更远,说明涡旋在高雷诺数的流动中需要更长的距离才能充分消散。边界层在分离现象发生过后,经过一定的距离又重新附着于床面。从图7中可以明显看到,在高雷诺数的流动中,再附着点的位置要更加靠前,再附着点后的边界层内部发展更为迅速,流动出现转捩,边界层内近壁一侧很快形成涡流的层流边界层并沿程逐渐发展,垂向上逐渐由层流转变为湍流。对于低雷诺数下的流动,再附着点的位置则相对靠后,且边界层内层流发展较缓,过渡区域的距离要大于高雷诺数的情况。 再附着点的位置表明,在同等条件下,回流区的长度比受来流雷诺数的影响。回流区长度比随雷诺数和波陡的变化如图8所示。图8(a)说明,当湍流在背流面形成回流区时,雷诺数越大,则回流区的长度比越小,这与文献[16]中对后台阶流动的研究结果是相符的。但有所不同的是,在后台阶流动中,台阶下游是平坦床面,涡旋脱落之后不受地形影响可以自由充分地发展,直至动量耗尽,尤其是在低雷诺数下回流区的发展既不受涡旋尾迹影响也不受地形约束,其长度在低雷诺数的情形下要比沙波湍流中的回流区长度大;沙波湍流的回流区更类似于高雷诺数下的后台阶流动,此时的涡旋尾迹影响范围广,涡旋向两侧流层的扩散作用强,向床面一侧的扩散开始受到地形的约束,因此,两者的回流区长度十分接近。 图8 回流区长度比随雷诺数和波陡的变化 各测量断面的湍动能分布如图9所示。对比工况2、工况4和工况5,观察图9各断面湍动能的分布可以看出,对相对水深y/h>0.32的主流而言,湍动能的大小均维持在了10-5至10-4量级之间,各工况之间差异极小,波陡在一定范围内的改变不会导致主流湍动能发生变化。 图9 各测量断面的湍动能分布 而对于剪切层以下的区域,由图9可以看到,湍动能较强的位置随着波陡的增大而向上移动,湍动能峰值位置与沙波波峰位置处于同一水平线上,流动的湍动强度也略有增强。在来流雷诺数不变的情况下,波陡增大使得回流区的高度随之上升至与波峰齐高,回流区的长度则相应减小,边界层得以更快地重新附着到床面的位置。从图8(b)中也可以看出,回流区的长度比随着波陡的增大而逐渐降低,但这种趋势会逐渐减弱,可以预测最终回流区的长度将保持不变。 不同迎、背流面水平距离比值(a/b)下各断面流速差异如图10所示。从图10中可以看出,无论a/b的值多大,水流在越过波峰后都会发生边界层分离并引起逆压梯度进而造成回流,但是回流区的范围变化不大,边界层重新附着的位置(即回流区中止的位置)也都处于4*断面和5*断面之间,在高度超过1.5 cm时主流流速分布无差异。 沙波迎流面和背流面水平距离比值不同,会直接影响回流区的整体形态以及回流强度。当a/b比值较大时,回流区垂向较为扁平,回流强度不大,因此底部流速较小,且随垂直高度的增加很快恢复正向随主流趋于一致。从4*断面和5*断面位置可以看到,当a/b为1~3时,剪切层几乎贴近于床面,而其他沙波形态下同样位置处仍是迎流面,回流相比波峰处仅仅强度减小而并未完全消散,剪切层位置要略高。 而对于a/b比值较小的情况,回流区的形态要更加厚实,且回流中心更靠近背流面。观察a/b=6、a/b=2和a/b=1三组结果可以看出,背流面坡度较大会使得逆压梯度陡增,造成背流面处的回流强度相对较大,底部反向流速也增大,在a/b比值小的情况下,流速恢复至与主流一致所需的垂向距离要更大一些。 图10 不同迎、背流面水平距离比值(a/b)下各断面的流速曲线 1)沙波的存在使得背流面存在稳定的回流现象。沙波湍流中,地形的变化使得边界层在越过波峰之后发生了分离现象,逆压梯度导致背流面产生回流,回流区内流速较小而压强较大,对进入主流的边界层起到顶托的作用,边界层进入主流后与回流区发生强烈掺混,随着湍动能的耗散,边界层在一段距离后会重新附着于床面。 2)回流区的形态受上游来流条件控制。来流雷诺数越大,流动的湍动作用便越强,边界层离开壁面后对涡旋的猝发效果也随之增强。边界层与回流区的交界区域,由于强烈的掺混作用会形成涡旋尾迹,其范围与雷诺数大小成正比。回流区的长度比在低雷诺数下要小于后台阶流动,而在高雷诺数的流动当中,两者回流区的长度比相近。 3)沙波波陡的变化直接影响回流区的高度。当来流条件相同时,主流区域的湍动能分布与波陡的高低无关;但在剪切层以下,湍动作用强烈的区域会随着波陡的增大而向上移动,回流区高度增长至与波峰平齐,其长度比随之减小,但这种趋势会随着波陡的进一步增大而逐渐减弱。 4)而沙波迎流面与背流面的水平距离之比a/b对回流区长度的影响不大,对回流区的高度有一定影响。a/b较大时,回流区形态细薄,回流主要发生在贴近床面的位置;a/b较小时,回流区的强度较大,形态也较为厚实,回流中心也更靠近背流面。1.4 模型建立
1.5 模型验证
2 结果与分析

2.1 沙波湍流的水流结构
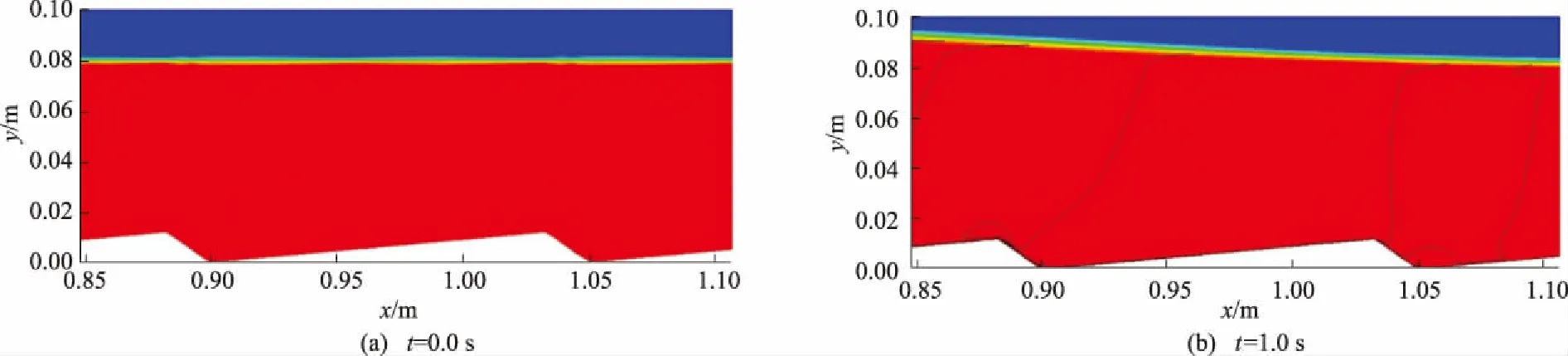
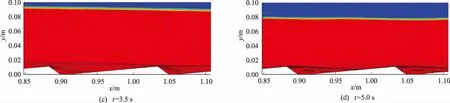

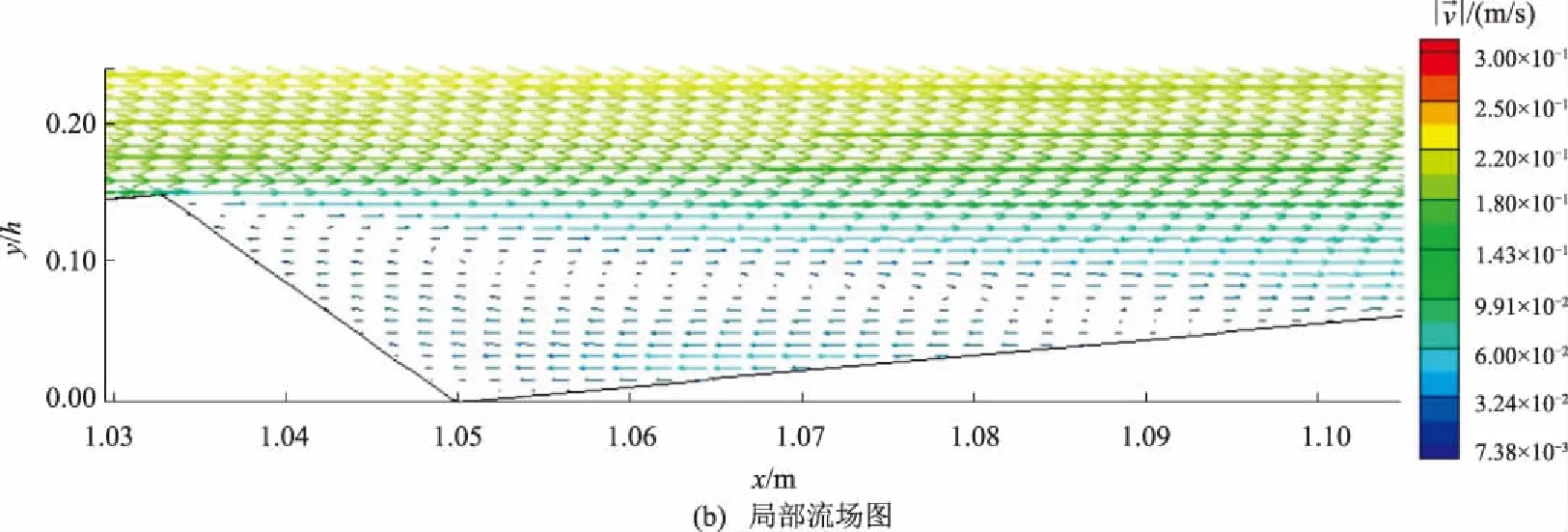

2.2 雷诺数Re对沙波湍流的影响
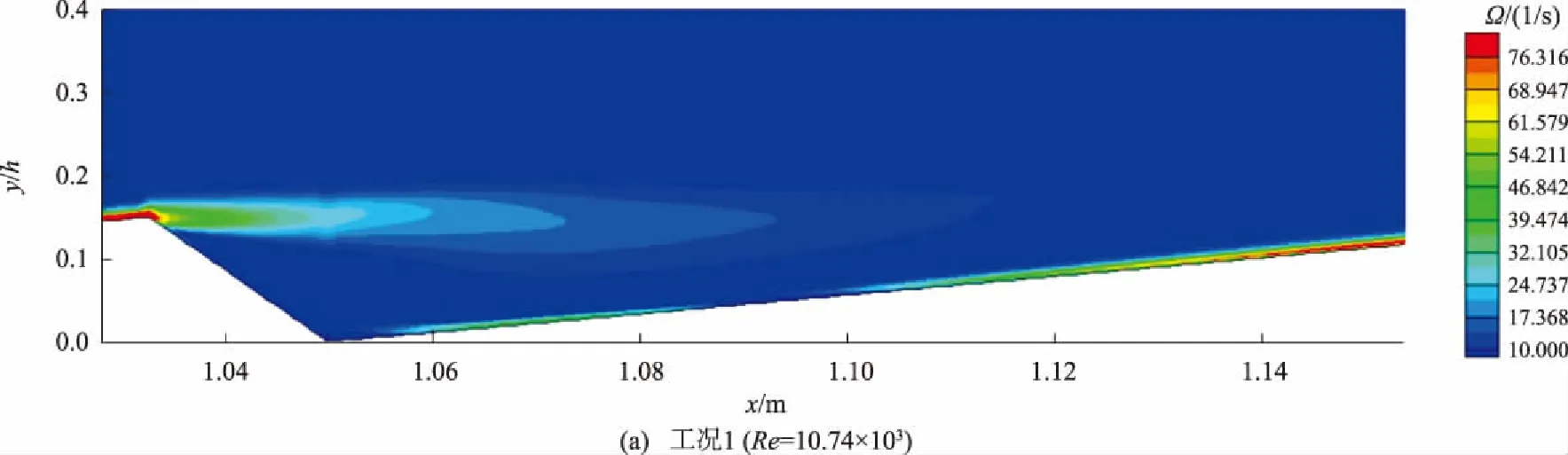
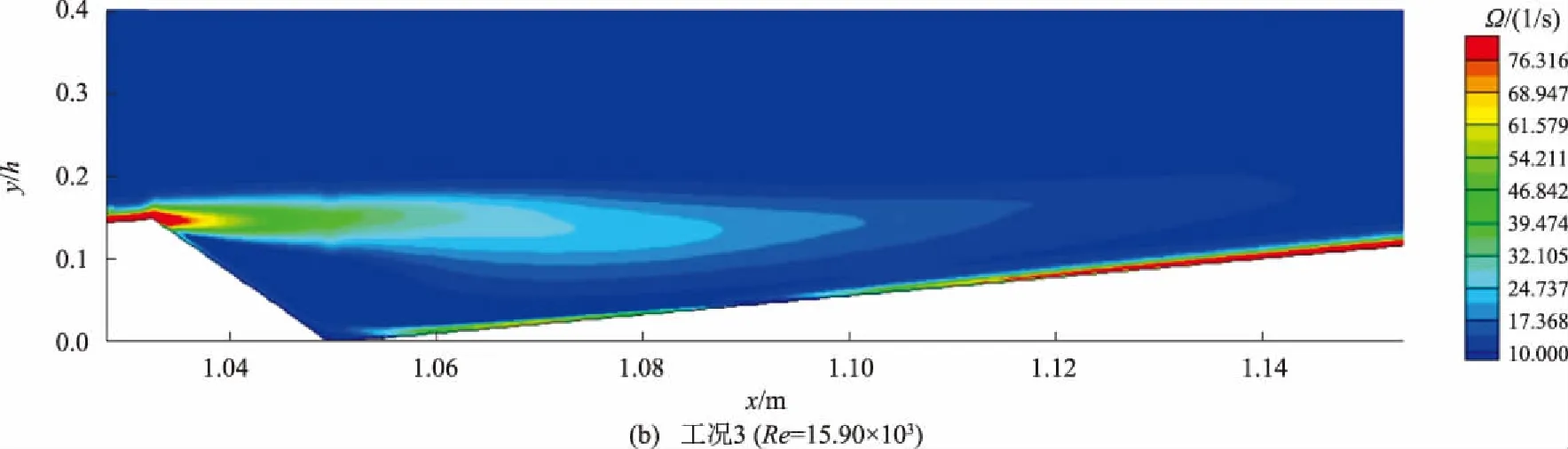

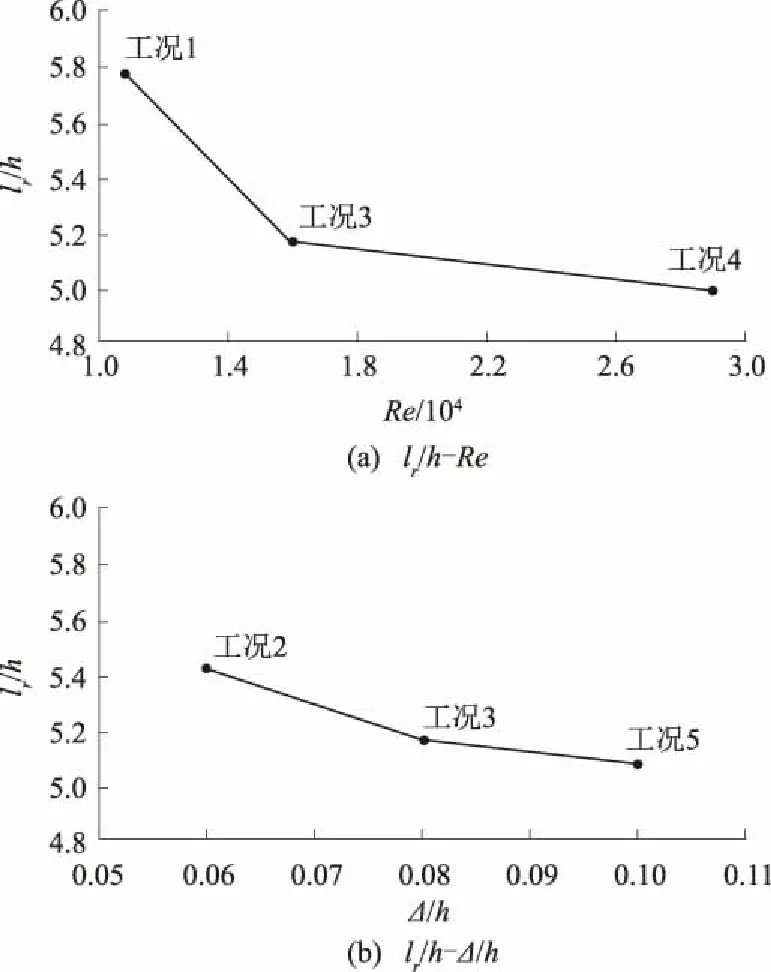
2.3 沙波形态Δ/λ与迎、背流面水平距离比值a/b对沙波湍流的影响
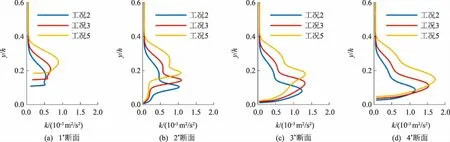
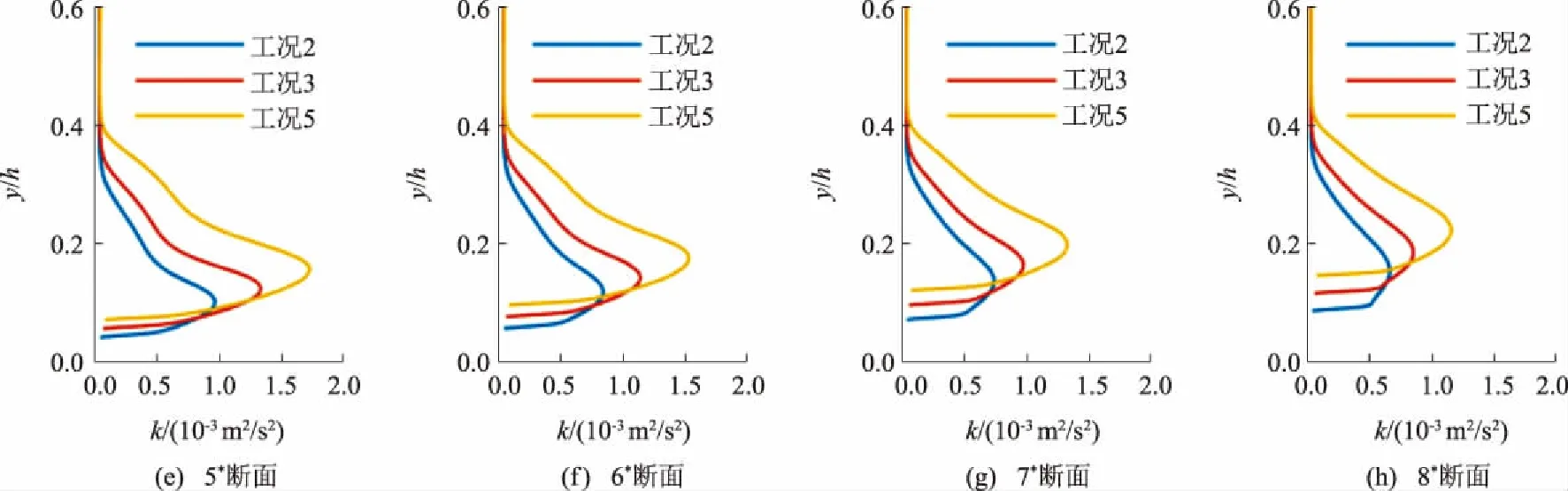


3 结语

