鱼鳞状床面粗糙特性

潘云文，刘 欣，杨克君

(1.武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072； 2.四川大学 水力学与山区河流开发保护国家重点实验室，成都 610065； 3.华北水利水电大学 水利学院，郑州 450046)

1 研究背景

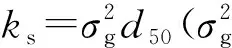
山区河床卵石表层长期经受水流的冲刷与分选，其颗粒外形大多扁平且在小范围内其级配组成也相对均匀。形状扁平的卵石在水流驱动作用下极易沿水流方向倾斜相靠、交错搭叠，形成“藏尾露头”的鱼鳞状床面(见图1)。鱼鳞状床面也是天然河流中十分常见的一种床面类型，它最突出的特点便是其颗粒排列具有明显的空间趋向，这在分析其粗糙特性时是该给予重点关注的。然纵观已有成果，未见有人专门探讨过鱼鳞状卵石床面的粗糙特性，这既不利于对床面复杂精细结构认识的深入，也有碍于河流动力学的发展，因此开展鱼鳞状卵石床面粗糙特性的专项研究是很有必要的。欲研究鱼鳞状床面的粗糙特性，首先须获得鱼鳞状床面。鱼鳞状床面的获取主要有3种方式：①直接去天然河道中找寻；②通过水槽试验塑造；③人工铺制。考虑到水流塑造鱼鳞状床面的形成除了与颗粒的几何形状参数有关外，还依赖于特殊的水流条件。在水槽试验中要产生这样的水流条件常常是困难的，甚至有时受试验条件所限，根本就形不成鱼鳞状床面，而野外实测又成本过高，因此本文人工铺制鱼鳞状床面，依托激光扫描技术获得其精确数字高程，基于统计学理论与分形理论对其粗糙特性进行探讨。与天然河道中的鱼鳞状床面相比，人工铺制鱼鳞状床面固然是一种简单的概化，但只要突出其颗粒排列具有明显空间趋向这一特点，那么研究成果对深化床面粗糙特性的规律认识、建立床面复杂精细结构的定量数学表达也是大有裨益的，同在水利工程实践中也具有广阔的应用前景。

图1 天然河道鱼鳞状床面Fig.1 Imbricate bed surface in a natural river channel

2 资料与方法

2.1 试验资料

图2 床面铺制与激光扫描Fig.2 Paving and laser scanning of experimental bed surfaces

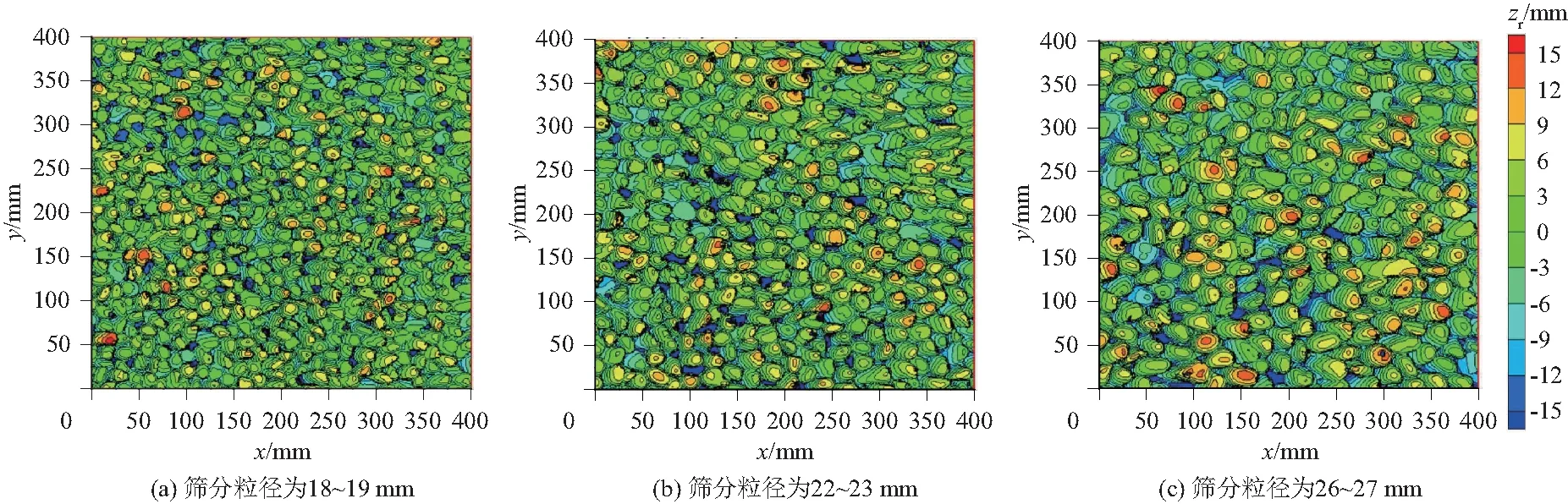
图3 床面数字高程Fig.3 Digital elevations of experimental bed surfaces

2.2 分析方法

2.2.1 统计参数

床面高程统计参数主要包括极差(R)、方差(σ2)、偏度(Sk)与峰度(Ku)，其值可分别由式(1)—式(4)计算。极差表征的是样本的取值范围；方差反映的是样本系列相对于样本均值的绝对偏离程度；偏度衡量样本频率分布的对称性，Sk> 0为正偏态，Sk< 0为负偏态，Sk=0为对称分布；峰度描述样本频率分布的陡缓，正态分布时Ku=3，高狭峰时Ku>3，低阔峰时Ku<3。

R=max{zi}-min{zi} ；

(1)

(2)

(3)

(4)

2.2.2 变异函数及其特征参数

变异函数γ通常由式(5)计算。

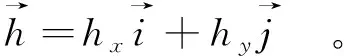
(5)

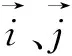
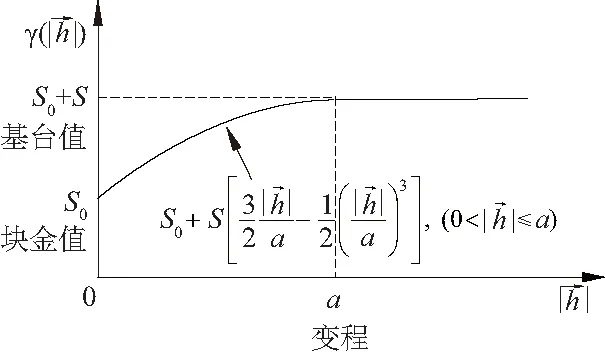
图4 变异函数球状模型Fig.4 Spherical model of variogram

(6)

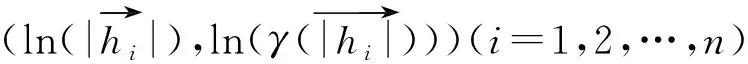
(7)

D=3-α/2 。

(8)

3 结果与讨论

3.1 床面相对高程频率分布与统计参数

由图5可知，鱼鳞状床面的相对高程频率分布具有明显的双峰特征，主峰近似正态且较为“高大”，次峰却极为“矮小”。然而床面相对高程频率分布的整体态势是呈负偏态的，而这种负偏态是由次峰的离群效应所造成的。次峰的出现绝非偶然，而是有深刻物理意义的，其所反映的实际是数值较小的高程点数相对于床面高程采样总数的占比，也就是床面颗粒间孔隙的高程频率。换句话说，床面相邻颗粒间的随机孔隙是造成鱼鳞状床面相对高程频率分布具有负偏双峰特征的根本原因。不难发现，随着卵石粒径的增大，主峰变得“矮胖”，次峰出现衰减，这与床面相邻颗粒间的随机孔隙同样密切相关。卵石粒径增大，床面最大凸起高度与最大孔隙深度相应增大，故而床面相对高程的频率分布跨度增大、高度减小，即主峰变得“矮胖”。卵石粒径增大而导致的次峰衰减同样具有明确的物理内涵。次峰的大小在一定程度上反映了床面孔隙率的大小。当卵石粒径较大时，实际研究区域俯视面积的绝大部分已为卵石实体所占据，这便使床面粒间孔隙的平面分布密度(单位面积的孔隙个数)减小，即床面孔隙率减小，故而次峰才出现衰减。换句话说，用均匀卵石人工铺制的单层鱼鳞状床面孔隙率会随着卵石粒径的增大而减小。由于次峰反映的是床面颗粒间的孔隙高程频率，因而次峰虽小，其对床面粗糙度的影响却是不可忽略的。当水流与床面发生作用时，卵石颗粒间的孔隙必定为水所充满，但由于卵石颗粒对其间孔隙的隐蔽与遮挡，孔隙中的水体流速较低。孔隙水的滞留填充了床面的凹陷，这是会对床面产生平滑效应的。如前所述，卵石粒径越小，利用其所铺床面的孔隙率越大，因而由孔隙水的滞留而产生的填充作用与平滑效应也就越明显，这也是粒径较小的床面粗糙度也较小的一个原因。总而言之，卵石颗粒与其间孔隙作为构成床面的基本要素，它们既相互区别，又相互联系，不存在无孔隙的床面，也不存在独立于颗粒的孔隙，二者完全是辩证而统一的。因此，在分析卵石床面粗糙特性时是不能完全割裂卵石颗粒与其间孔隙的共存关系的。

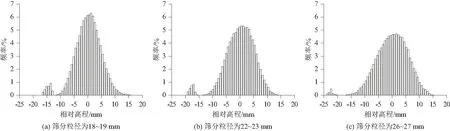
图5 床面相对高程频率分布Fig.5 Frequency distributions of relative elevations of experimental bed surface

由图6可知，鱼鳞状床面相对高程频率分布的偏度均<0，峰度均>3，其中偏度整体上随卵石粒径的增大而减小，峰度随粒径的增大而增大。换句话说，鱼鳞状床面相对高程频率分布整体上呈负偏态、高狭峰，且粒径越大，其负偏特征越明显。但整体的高狭峰特征仅仅是一个表象，因为从相对频率分布图来看，其主峰始终是近似正态分布的，因此这种整体的高狭峰特征完全是由次峰的离群效应所产生的错觉。卵石粒径越大，其床面最大凸起高度与最大孔隙深度必定越大，因而其极差也越大。然由各拟合公式的相关系数的平方(R2)可知，极差、偏度、峰度与卵石粒径之间并不存在明确的线性相关性，它们对鱼鳞状床面相对高程频率分布整体态势的刻画只是一种十分粗略的近似。床面高程方差却不尽然，它与卵石粒径的线性相关性是十分明确的。这也就是说，床面高程方差可以作为鱼鳞状床面粗糙特性的优良表征，卵石粒径越大，床面高程方差越大，床面越粗糙，反之亦然。文献[5]曾研究过散叠型卵石床面的统计粗糙特性，其床面相对高程频率分布整体上呈负偏态、高狭峰，这与本文所铺鱼鳞状床面的高程频率分布特性是完全相同的，其原因就在于这两项研究所采用的三维激光扫描技术较为先进，能精确测量床面相邻颗粒间的孔隙形态，继而使得其后续分析能够充分考虑颗粒间的孔隙对床面粗糙度的贡献，这显然是测量技术的进步而带来的认识水平的提高。然而当卵石粒径相同时，散叠型卵石床面的负偏程度大于本文的鱼鳞状床面，这主要是由所铺卵石床面的层厚差异所引起的。考虑到卵石用量，本文所铺制的鱼鳞状床面是单层的，因而床面相邻颗粒间的最大孔隙深度较小，故而相对高程频率分布的负偏程度也较小。此外，当卵石粒径相同时，散叠型卵石床面的高程方差也大于鱼鳞状床面的对应值。这也就是说：当卵石粒径相同时，鱼鳞状床面的粗糙度小于散叠型床面的粗糙度。这便解释了为什么鱼鳞状排列的卵石会比松散排列的更难起动[15]。与散叠型卵石床面相比，鱼鳞状床面的粗糙度相对较小，当水流流过其表面，鱼鳞状床面施加于水流的阻力较小，因而水流给予鱼鳞状床面的反作用力也较小，故而其床面结构相对稳定，其颗粒较难起动。再者，鱼鳞状床面颗粒倾斜相靠、交错搭叠的排列方式会增强相邻卵石间的摩擦作用与隐蔽效应，这也是鱼鳞状床面相对稳定的一个原因。

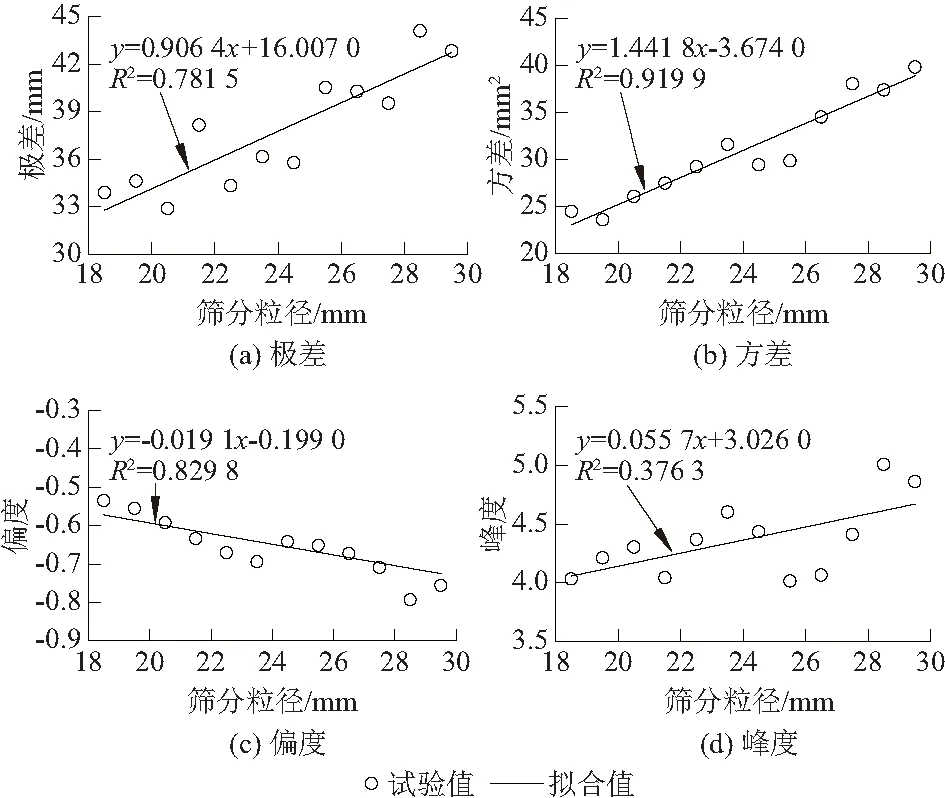
图6 床面高程统计参数Fig.6 Statistical parameters of experimental bed surface elevations

3.2 床面变异特性

由图7可知，鱼鳞状床面的高程变异函数与球状模型甚为接近，当计算尺度大于变程后仅表现出轻微的波动，球状模型可作为其粗糙特性量化的优良理论模型。随着卵石粒径的增大，各床面高程变异函数的基台值与变程均增大。基台值增大说明高程变化幅度增大，继而其床面更粗糙。变程增大说明床面组成颗粒的影响范围增大。将本文的鱼鳞状床面与文献[5]所述的散叠型床面进行对比，可以发现：当粒径相同时，在任一方向上，鱼鳞状床面的高程变异函数变程均大于散叠型床面的对应值。这说明鱼鳞状床面的颗粒影响范围更大，而这种差异无疑是由颗粒的鱼鳞状排列方式所造成的。由图8不难发现，变异函数稳定后，其值与床面高程方差是非常接近的，这说明床面高程方差与变异函数基台值在量化鱼鳞状床面粗糙特性方面是基本等价的。卵石粒径越大，床面高程方差越大，变异函数基台值越大，床面越粗糙，反之亦然。由图9可知，鱼鳞状床面不同计算方向的高程变异特性是有差异的，尤其是与x轴正向(相当于水流方向)的角度成0、π/4与π/2的3个方向，因此在分析鱼鳞状床面粗糙特性时，有必要对其颗粒排列的方向性给予足够的重视。

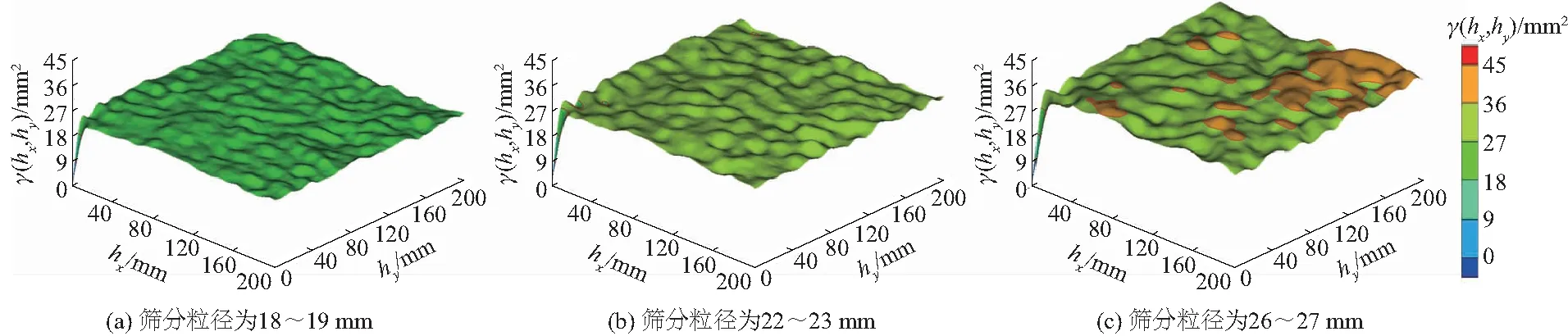
图7 床面高程二维变异函数Fig.7 Two-dimensional variograms of experimental bed surface elevations

图8 基台值与方差的关系Fig.8 Relevance between sill and elevation variances

图9 床面二维特征方向变异特性Fig.9 Variogram parameters in two-dimensional specific directions of experimental bed surfaces

3.3 床面分形特征

由图10可知，鱼鳞状床面二维特征方向无标度上限随卵石粒径的增大而单调增大，其值可近似取为0.5d50。然而，同一床面在与x轴正向(相当于水流方向)的角度成0、π/4与π/2的3个方向上无标度区是大致相同的，并不存在明显的方向上的差异。由图11可知，鱼鳞状床面二维特征方向分形维数具有明显的方向上的差异。对同一床面而言，在与x轴正向的角度成0的方向上分形维数最大，床面结构最复杂；在与x轴正向成π/2的方向上分形维数次之，床面结构较为复杂；在与x轴正向成π/4的方向上分形维数最小，床面结构相对简单。而就同一个二维特征方向而言，随着卵石粒径的增大，床面分形维数基本减小，床面结构复杂性减弱。这一现象的出现主要有两方面的原因，其一：在天然河道中，卵石的输移通常以推移的方式进行。卵石粒径越大，其推移运动的动量越大，与床底其它卵石的碰撞冲击作用越强烈，因而更易将其外形磨得圆滑。卵石圆滑的外形是有助于减弱床面结构复杂性的。其二：如前所述，随着卵石粒径的增大，实际研究区域俯视面积的绝大部分将为卵石实体所占据，床面粒间孔隙的平面密度(单位面积的孔隙个数)将减小，这也是有助于减弱床面结构复杂性的。

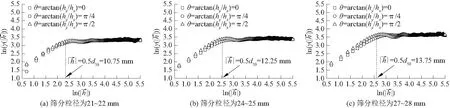
图10 床面二维特征方向无标度区判定Fig.10 Judgment for scale-free ranges in two-dimensional specific directions of experimental bed surfaces

图11 床面二维特征方向分形维数Fig.11 Fractal dimensions in two-dimensional specific directions of experimental bed surfaces

4 结 论

(1)鱼鳞状床面相对高程频率分布具有负偏双峰特征，主峰近似正态且较为“高大”，次峰却极为“矮小”。相对高程频率分布的负偏态是由次峰的离群效应所造成的，而次峰的离群效应又是由床面相邻颗粒间的随机孔隙所导致的。

(2)床面高程方差与卵石粒径的线性相关性是十分明确的，可以作为鱼鳞状床面粗糙特性的优良表征。卵石粒径越大，床面高程方差越大，床面越粗糙，反之亦然。

(3)与由相同粒径的卵石颗粒所铺制的散叠型床面相比，鱼鳞状床面的粗糙度较小，其床面结构相对稳定。

(4)球状模型可作为鱼鳞状床面统计粗糙特性量化的优良理论模型。卵石粒径增大，各床面高程变异函数的基台值与变程均增大。

(5)床面高程方差与变异函数基台值在量化鱼鳞状床面粗糙特性方面是基本等价的。

(6)鱼鳞状床面二维特征方向无标度区上限随卵石粒径的增大而单调增大，其值可近似取为0.5d50(d50为中值粒径)。然而同一床面各二维特征方向无标度区上限是大致相同的，并不存在明显的方向上的差异。

(7)就同一二维特征方向而言，随着卵石粒径的增大，床面分形维数基本减小，床面结构复杂性减弱。

(8)鱼鳞状床面粗糙特性具有明显的方向性，尤其是与水流方向的角度成0、π/4与π/2的3个方向，其粗糙特性明显不同。

(9)采用均匀卵石人工铺制的单层鱼鳞床面只是天然鱼鳞状床面的一种粗略概化，虽然该做法突出了颗粒排列具有明显空间趋向的这一特性，但并没有考虑级配组成、卵石扁平度与铺制层数对床面结构的影响；另外，水流塑造与人工铺制也肯定是存在差异的。因此，后来学者应充分考虑会对鱼鳞床面结构产生影响的因素，积极开展水槽试验，力求塑造出更为接近天然情况的鱼鳞状床面来进行研究；如果条件允许，争取去天然河道中实测。