梯形明渠边界平均剪切应力计算方法

曹京京，申红彬

(1. 黄河水利职业技术学院，河南 开封 475004；2. 北京市水科学技术研究院，北京 100048； 3. 北京师范大学 水科学研究院，北京 100875)

梯形明渠边界平均剪切应力计算方法

曹京京1，申红彬2, 3

(1. 黄河水利职业技术学院，河南 开封 475004；2. 北京市水科学技术研究院，北京 100048； 3. 北京师范大学 水科学研究院，北京 100875)

梯形断面是渠道设计中广泛采用的一种断面形式，边界剪切应力分布规律是研究水流结构及阻力特性的重要因素。经过理论推导，建立了梯形明渠床面与边壁平均剪切应力相对值随过水断面宽深比的计算表达式，并与多家试验资料进行了比较，结果表明两者变化趋势基本一致。针对梯形明渠不同边坡角下的水力最优断面，分析了其床面、边壁平均剪切应力的变化规律，发现随着边坡角的减小，床面平均剪切应力相对值变化不大，而边壁平均剪切应力相对值呈现出减小的趋势。

梯形明渠；床面平均剪切应力；边壁平均剪切应力；过水断面宽深比；水力最优断面

1 研究背景

明渠水流与二维水流(如圆管流、平板流等)在许多方面存在着本质的差别，主要表现在随着断面宽深比的减小及边壁影响程度的不断增大，水流呈现出三维流动的特性。明渠剪切应力沿边界的分布规律是研究水流结构及阻力特性的重要因素，对水流中的泥沙运动、污染物输移规律等具有重要的影响，是渠道工程设计及理论研究的基本问题之一。

根据Rajaratnam等[1]、Ghosh等[2]、Knight等[3]、胡春宏等[4]的一系列水槽试验结果表明，明渠过水断面形式是决定边界剪切应力分布的主要影响因素，与弗汝德数Fr无关。其中，矩形明渠床面与边壁平均剪切应力的相对值仅与断面宽深比有关，这实质上反映出床面与边壁的不同影响。对于明渠床面与边壁影响区的划分，不同的学者提出了不同的方法。Keulegan[5]提出采用明渠2个底角的角平分线划分过水断面床面与边壁影响区。Einstein[6]采用水力半径分割法将明渠过水断面划分为床面影响区和边壁影响区，各区域内水体分别与对应边界上的剪切力相平衡。杨树清[7]认为明渠床面与边壁影响区的分割线是由通过床面与边壁交点的一系列到床面与边壁相对水力距离相等的点所组成，并推导得出了矩形明渠床面与边壁平均剪切应力的计算表达式。胡旭跃等[8]在杨树清[7]分割法的基础上，通过与试验资料适配进行了改进。Guo等[9]通过对明渠均匀流微分连续方程与动量方程联合近似求解，推导得到了矩形明渠床面与边壁平均剪切应力计算的近似解。申红彬等[10]从明渠水流过水断面水体微团能量二维输送权重角度出发，推导得到了矩形光滑或均匀粗糙明渠床面与边壁影响区分割线的二次近似表达式，并通过积分运算得到床面与边壁平均剪切应力的计算表达式。

概括对以往明渠床面与边壁影响区的分割方法特点： ① Keulegan、杨树清的分割线以及胡旭跃等的改进线型均为直线，形式过于简单，理论假定的合理性也有待商榷；② Einstein方法只是模糊而笼统地给出了虚拟的分割面积；③ Guo等基于简化方程及坐标变换虽然具有一定的数学理论基础及物理意义，但得到的分割曲线形式较为复杂，难以在工程实际中推广应用；④ 申红彬等的分割曲线形式介于简单与复杂之间，具有一定的物理基础，剪切应力计算结果也与实测试验数据较为相符。

明渠过水断面的形式包括矩形、梯形与复式断面。其中，梯形是渠道设计中广泛采用的一种断面形式。以往研究对象多为矩形光滑或均匀粗糙明渠，断面形式略显单一。笔者在上述研究成果的基础上，进一步研究梯形明渠床面与边壁平均剪切应力的计算方法与变化规律。

2 梯形明渠床面与边壁影响区的划分

对于梯形明渠，以最大流速点为坐标原点o，垂直床面方向为y轴，平行床面方向为z轴，α为边坡角，考虑到过水断面的对称性，取一半建立yoz坐标系，如图1所示。

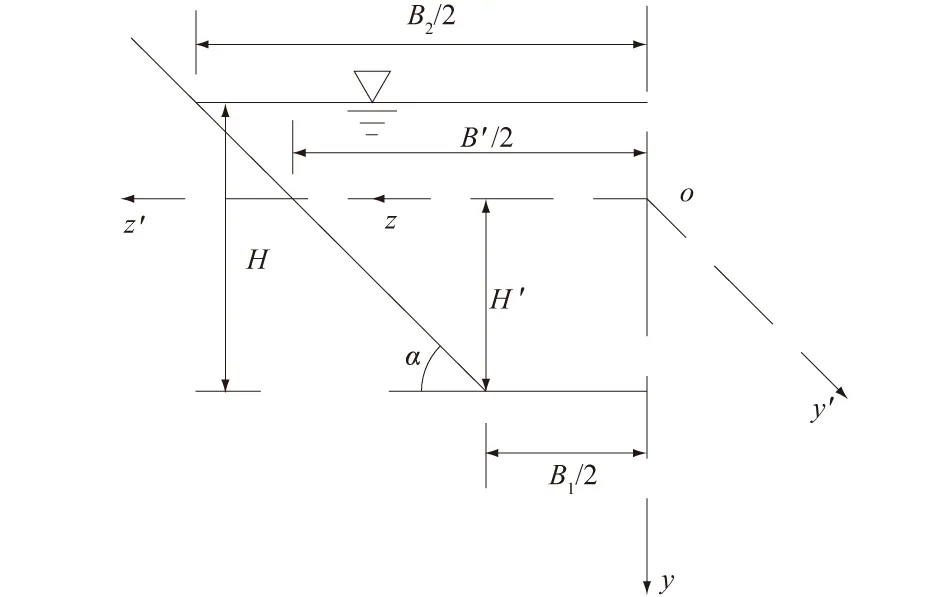
图1 梯形明渠过水断面坐标系Fig.1 Coordinate system of trapezoidal open channel

根据文献[10]，明渠过水断面床面与边壁影响区分割线的微分方程为

(1)

式中τw，τb分别为左侧及底部剪切应力。

将微分方程(1)的解近似表示成二次多项式结构为

y≈az2+bz+c 。

(2)

式中a，b，c为系数。

明渠过水断面床面与边壁影响区的分割曲线应通过床面与边壁的交点和坐标原点。在坐标原点处，由于明渠过水断面沿中心轴y轴的左右对称性，分割曲线的导数等于0。在床面和边壁交点处，床面与边壁的受力情况主要与其表面的粗糙程度有关，对于光滑或均匀粗糙明渠，有τb=τw。

在图1中，进一步以与床面平行方向为z′ 轴，与边壁平行方向为y′ 轴，建立y′oz′坐标系。yoz坐标系与y′oz′坐标系之间存在如下坐标变换关系：

y=y′sinα ；

(3)

z =z′-y′cosα 。

(4)

对于光滑或均匀粗糙梯形明渠， 在y′oz′坐标系下，在床面和边壁交点处为

(5)

则在yoz坐标系下，梯形明渠过水断面床面与边壁影响区分割线在床面和边壁交点处的导数为

(6)

根据文献[10]中矩形明渠过水断面床面与边壁影响区分割线的求解方法，可以求出yoz坐标系下梯形明渠过水断面床面与边壁影响区分割线的二次近似表达式如式(7)、式(8)。

(7)

(8)

式中：B1，H，α分别为梯形明渠底宽、水深、边坡角。

3 梯形明渠过水断面边界平均剪切应力计算表达式

根据式(7)、式(8)，通过积分运算，可以分别得到梯形明渠床面及边壁影响区域的面积与水力半径，进而可以求出床面及边壁平均剪切应力与边界平均剪切应力相对值的计算表达式，即：

(9)

(10)

根据Knight等[11-12]梯形均匀粗糙明渠床面、边壁平均剪切应力相对值实测资料，分别对梯形明渠过水断面床面、边壁平均剪切应力相对值计算表达式(9)、式(10)进行检验，如图2所示。另外，图3分别给出了当边坡角α=90°时，对应矩形明渠过水断面床面、边壁平均剪切应力相对值计算值与实测值的对比情况。

图2 梯形明渠床面、边壁平均剪切应力计算结果Fig.2 Calculation results of average shear stress of the sidewall and bed of trapezoidal open channel

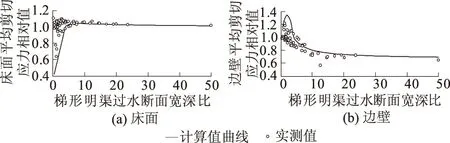
图3 矩形明渠床面、边壁平均剪切应力计算结果Fig.3 Calculation results of average shear stress of the sidewall and bed of orthogonal open channel

从图2、图3可以看出，根据式(9)、式(10)计算得到的一般梯形与矩形明渠过水断面床面、边壁平均剪切应力与边界平均剪切应力相对值的变化规律与实测数据的变化趋势基本一致。因此，式(9)、式(10)的计算适用范围更广，可以用来计算不同边坡角下梯形明渠的床面与边壁平均剪切应力。

4 梯形明渠水力最优断面边界平均剪切应力变化规律

在渠道设计中，底坡一般由地形条件所决定，糙率取决于渠壁材料，故渠道输水能力只取决于过水断面大小和形状。对于梯形明渠，水力最优断面宽深比的计算表达式为

(11)

式中βh为梯形明渠水力最优断面宽深比。

根据梯形明渠床面与边壁平均剪切应力的计算表达式(9)、式(10)，可以得到梯形明渠不同边坡角下床面、边壁平均剪切应力相对值随过水断面宽深比的变化规律，同时基于式(11)可以进一步得到不同边坡角下水力最优断面床面、边壁平均剪切应力的变化规律，如图4所示。

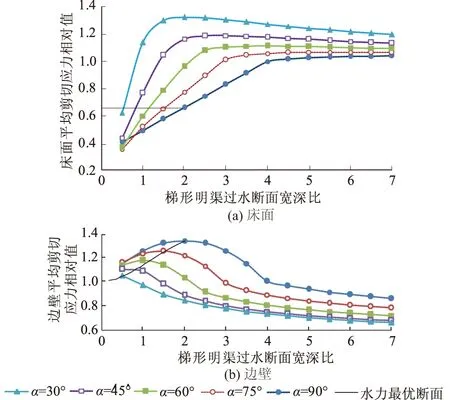
图4 梯形明渠水力最优断面床面、边壁平均剪切应力变化情况Fig.4 Variations of average bed shear stress and average sidewall shear stress of the optimum section of trapezoidal channel

从图4可以看出：①对于梯形明渠，随着边坡角的减小，床面平均剪切应力所占比重逐渐增大，而边壁平均剪切应力所占比重逐渐减小；②梯形明渠不同边坡角下水力最优断面均位于相对窄深断面区域；③对于梯形明渠，随着边坡角的减小，床面平均剪切应力相对值变化不大，基本在0.66左右，而边壁平均剪切应力相对值呈现出减小的趋势。

5 结 论

(1) 经过理论推导，建立了梯形明渠床面与边壁平均剪切应力相对值随过水断面宽深比的计算表达式，并与多家试验资料进行了比较。结果表明两者变化趋势基本相符，可以用来计算不同边坡角下梯形明渠的床面与边壁平均剪切应力。

(2) 对于梯形明渠，随着边坡角的减小，床面平均剪切应力所占比重逐渐增大，而边壁平均剪切应力所占比重逐渐减小。

(3) 梯形明渠不同边坡角下水力最优断面均位于相对窄深断面区域，而且随着边坡角的减小，床面平均剪切应力相对值变化不大，而边壁平均剪切应力相对值呈现出减小的趋势。

[1]RAJARTNAM N, MURALIDHAR D. Boundary Shear Stress Distribution in Rectangular Open Channels [J]. La Houille Blanche, 1969, 24(6): 603-609.

[2]GHOSH S N,ROU N. Boundary Shear Stress Distribution in Open Channel Flow [J]. Journal of Hydraulic Division, ASCE, 1970, 96(4): 839-851.

[3]KNIGHT D W,MACDONALD J A.Open Channel Flow with Varying Bed Roughness [J]. Journal of Hydraulic Division, ASCE, 1979, 105：1167-1183.

[4]胡春宏,倪晋仁.矩形明槽中断面紊流流速分布规律的初步研究[J]. 水利水运科学研究, 1988, (2): 27-36.

[5]KEULEGAN G K.Laws of Turbulent Flow in Open Channels Research Paper Report1151[R]. Washinton, D. C.: National Bureau of Standards, U. S. Department of Commerce, 1938: 707-741.

[6]EINSTEIN H A.Method of Calculating the Hydraulic Radius in a Cross section with Different Roughness[J]. Transactions of ASCE, 1942, (107): 575-577.

[7]杨树清.论矩形明渠流边界切应力分布规律[J].泥沙研究, 1993, (3): 95-103.

[8]胡旭跃,曾光明,黄国和,等.矩形明渠边界平均剪切应力变化规律研究[J]. 泥沙研究, 2002, (4): 42-47.

[9]GUO J K,JULIEN P Y.Shear Stress in Smooth Rectangular Open-channel Flows [J]. Journal of Hydraulic Engineering, ASCE, 2005, 131(1): 30-37.

[10]申红彬,张小峰,乔 伟.明渠水力半径分割线及边界平均剪切应力[J]. 水力发电学报, 2011, 30(1): 44-48.

[11]KNIGHT D W, AL-HAMID A A I, YUEN K W H.Boundary Shear in Differentially Roughned Trapezoidal Channels[C]∥Hydraulic and Environmental Modelling: Estuarine and River Waters. Proceedings of the Second International Conference on Hydraulic and Environmental Modelling of Coastal, Estuarine, and River Waters. UK: Ashgate Press, 1992: 3-14.

[12]KNIGHT D W,YUEN K W H,AL-HAMID A A I. Boundary Shear Stress Distribution in Open Channel Flow[M]∥BEVEN K J, CHATWIN P C, MILLBANK J H. Mixing and Transport in the Environment, Chichester: J. Wiley, 1994: 51-87.

(编辑：王 慰)

Method of Calculating Average Boundary Shear Stress inTrapezoidal Open Channels

CAO Jing-jing1, SHEN Hong-bin2,3

(1.Yellow River Conservancy Technical Institute, Kaifeng 475004, China; 2.Beijing Water Science and Technology Institute, Beijing 100048, China; 3. College of Water Sciences, Beijing Normal University, Beijing 100875, China)

Trapezoidal section is widely used in the design of channels. The regularity of boundary shear stress distribution is an important factor in the research of flow structure and resistance.In this article, the expressions of the relative values of average bed and sidewall shear stress with width-depth ratio of flow section are derived through integration. Comparison between the present calculation method and Knight’s experimental data reveals relatively small error. The variation regularity of average bed and sidewall shear stresses of optimal hydraulic section in trapezoidal open channels with different side angels is analyzed. The result shows that the optimal hydraulic section in trapezoid open channel is narrow and deep, the average bed shear stress changes little while the average sidewall shear stress reduces with the decrease of side angel.

trapezoidal open channel; average bed shear stress; average sidewall shear stress; width-depth ratio of flow section; optimal hydraulic section

2015-05-17；

2015-09-11

曹京京(1981-), 女, 河南开封人, 讲师, 主要从事水利工程设计、水工建筑材料检测方面的教学与研究工作, (电话)13937862885(电子信箱)405376748@qq. com。

10.11988/ckyyb.20150416

2016,33(12):51-54

TV14

A

1001-5485(2016)12-0051-04