调谐惯容阻尼器对斜拉索振动控制的研究

郜辉, 汪志昊

(华北水利水电大学 土木与交通学院,河南 郑州 450045)

大跨度斜拉桥的斜拉索极易在外界环境激励下产生多种有害振动,持续、大幅的斜拉索振动不仅会引起拉索的疲劳损伤,而且会破坏斜拉索的防腐系统,进而降低斜拉索的服役寿命,并增加整个桥梁结构的维护成本。因此,有必要研究有效的斜拉索振动控制技术来降低斜拉索振动带来的危害。安装外置黏滞阻尼器(Viscous Damper,VD)是一种应用最为广泛的斜拉索减振措施,但其减振效果受到安装高度的制约[1-4],对超长斜拉索提供的附加阻尼有限。

为提升VD对斜拉索的减振效果,基于磁流变(Magnetorheological,MR)阻尼器的智能、半主动控制措施被逐渐提出[5-8]。研究结果表明[9-12]:负刚度阻尼器可以显著提升斜拉索的减振效果。近几年，具有负刚度效应的惯质阻尼器得到了较多关注:LU Lei等[13]、SHI Xiang等[14]开展了黏滞惯质阻尼器(Viscous inertial Mass Damper,VMD)对斜拉索减振控制的仿真分析和参数优化研究;汪志昊等[15]采用电磁式惯质阻尼器试验验证了VMD对斜拉索的减振提升效果,并指出VMD的减振性能提升主要归功于惯容单元有助于放大阻尼单元的位移,从而实现了VMD整体耗能能力的提升。

为进一步提升斜拉索的减振效果,本文基于“阻尼-惯容-弹簧”三元被动减振理论[16],开展了调谐惯容阻尼器(Tuned Inerter Damper,TID)对斜拉索减振性能的提升研究。基于复模态理论,分析了TID惯容比、阻尼比、频率比对斜拉索模态阻尼比的影响,获得了TID的最优调谐参数与斜拉索的最大附加模态阻尼比。通过对比TID、VMD和VD对斜拉索的减振效果,阐明了TID对斜拉索减振控制的优越性。最后，基于耗能效率揭示了TID对斜拉索的减振增效机理。

1 斜拉索-TID系统状态空间方程

忽略斜拉索垂度和抗弯刚度的影响,斜拉索-TID耦合系统的分析模型如图1所示,其中TID由阻尼单元并联弹簧单元后再串联惯容单元构成。参照文献[4],斜拉索-TID耦合系统的振动微分方程可表示为:

(1)

式中:m为斜拉索单位长度的质量;u(x,t)为斜拉索在t时刻x位置处的横向位移;T为斜拉索的张力；xd为TID的安装位置距离斜拉索左侧锚固端的距离;δ(·)为Dirac Delta函数;FTID为TID作用于斜拉索的横向力。FTID可表示为:

(2)

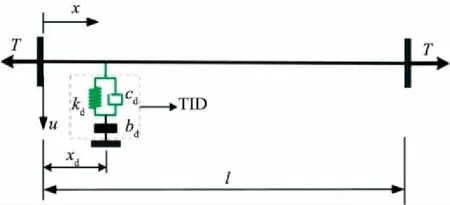
图1 斜拉索-TID耦合系统分析模型

采用有限差分法,考虑斜拉索两端的边界条件:

(3)

式中l为斜拉索的长度。斜拉索-TID耦合系统的运动微分方程可表示为:

(4)

M=maIn,C=0n，

(5)

(6)

式中:M、C、K分别为斜拉索的质量矩阵、阻尼矩阵和刚度矩阵；In为n阶单位矩阵;n为离散斜拉索的内节点个数;a=l/N,为斜拉索单元长度;N为斜拉索的单元个数,N=n+1;u和f分别为斜拉索的位移向量和外荷载向量;γ为TID的作用位置向量；ui和fi分别为斜拉索第i个节点的位移和外荷载;γi由TID的安装位置决定。当TID安装在斜拉索第k个节点时,有

(7)

当在x=xd位置安装VMD或VD时,斜拉索-阻尼器耦合系统的运动微分方程可表示为:

(8)

式中:Md=M+γbdγT、Cd=C+γcdγT，分别为斜拉索-阻尼器耦合系统的质量矩阵和阻尼矩阵；bd和cd分别为VMD的惯容系数和阻尼系数,且bd=0时VMD将退化为VD。

为形成斜拉索-TID耦合系统的运动微分方程,将式(2)中的FTID重写为:

(9)

综合式(4)和式(9),斜拉索-TID耦合系统的运动方程可表示为:

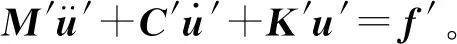
(10)

(11)

方程(8)和(11)的状态空间方程可表示为:

(12)

对于VMD和VD有:

(13)

对于TID有:

(14)

2 斜拉索-TID耦合系统复模态分析

2.1 耦合系统模态阻尼比

设斜拉索-阻尼器耦合系统自由振动时状态向量可表示为:

z=Zexp(pt)。

(15)

式中：Z为状态向量z的幅值；p为矩阵A的特征值。将式(15)代入式(12)并移去外荷载,可得斜拉索-阻尼器耦合系统的特征方程如下：

AZ=pZ，

(16)

(17)

式中：ωk和ζk分别表示斜拉索-阻尼器耦合系统第k阶模态的振动圆频率和阻尼比。

根据式(17),斜拉索-阻尼器耦合系统的第k阶模态的振动圆频率和模态阻尼比可分别表示为:

(18)

式中Re(p)和Im(p)分别为p的实部和虚部。

对于VD和VMD,斜拉索第k阶模态的附加模态阻尼比可直接由式(18)计算。对于斜拉索-TID系统,TID的调谐作用将使斜拉索的某一阶模态转化为斜拉索-TID耦合系统的2个相近模态,为有效抑制斜拉索振动,应取2个相近模态的附加模态阻尼比的较小值作为TID提供的斜拉索附加模态阻尼比。

2.2 参数分析

TID的阻尼系数、弹簧刚度和惯容系数均会影响斜拉索-TID耦合系统的模态阻尼比,为使分析更具普适性,引入下列无量纲参数:

(19)

式中:μ为TID的无量纲惯容比；ωd为TID自身的振动圆频率；f为TID的无量纲频率比；ξd为TID的无量纲阻尼比。

图2为斜拉索附加模态阻尼比随TID阻尼比和频率比的变化曲线。由图2可知:斜拉索附加模态阻尼比随TID阻尼比和频率比的变化呈先增大后减小的变化趋势,存在最优的阻尼比和频率比;随着TID阻尼比的变化,TID最优频率比基本保持不变。

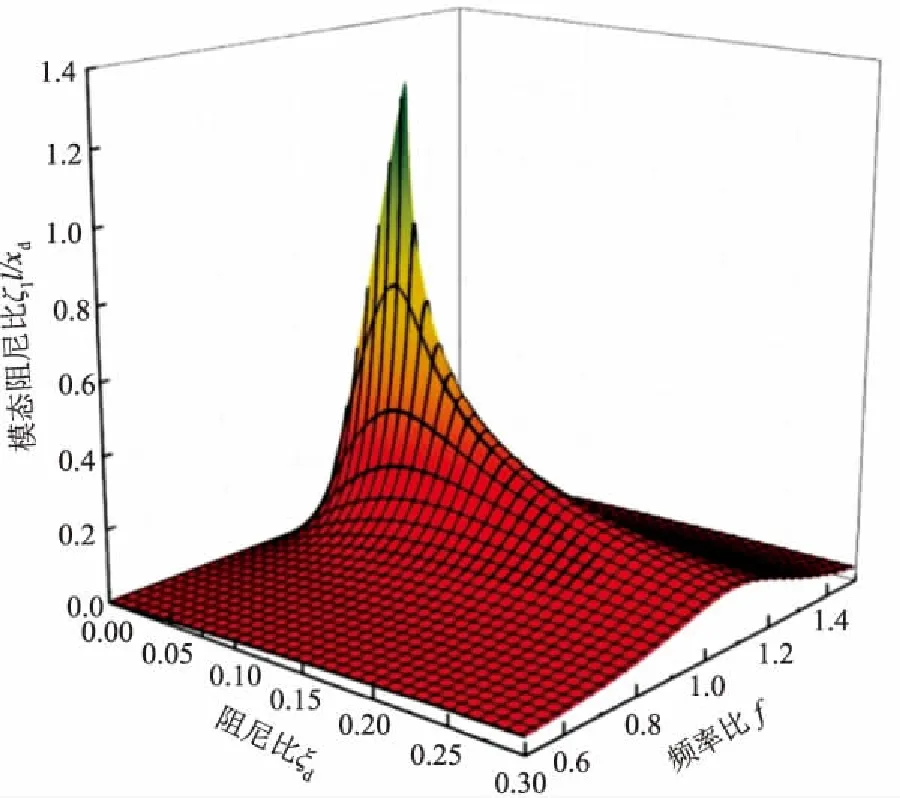
图2 斜拉索附加模态阻尼比随TID阻尼比和 频率比的变化关系(μ=0.5,xd/l=0.02)

在此基础上,图3给出了TID最优频率比和最优阻尼比以及斜拉索获得的最优附加模态阻尼比随TID惯容比的变化关系。

图3 TID最优频率比、阻尼比以及斜拉索最优附加模态阻尼比随TID惯容比的变化关系(xd/l=0.02)

图3(a)表明,TID各阶模态最优频率比随惯容比的增大而变化的情况分为3个阶段:第1阶段,TID的最优频率比随着惯容比的增大而缓慢增大至最大值;第2阶段,TID的最优频率比随着惯容比的增大从最大值迅速下降至0;第3阶段,TID的最优频率比始终保持为0,此时TID将退化为一种新阻尼器,即由阻尼单元串联惯容单元构成的SVMD。为了阐述方便,将TID最优频率等于0时对应的惯容比称为临界惯容比。

图3(b)表明:当TID惯容比小于临界值时,TID最优阻尼比随着惯容比的增大而增大;当TID惯容比大于临界值时,TID最优阻尼比随着惯容比的增大而减小。TID的最优阻尼比在临界惯容比位置不可导,这主要是由于TID退化为SVMD后,两种阻尼器为斜拉索提供的附加模态阻尼比随阻尼器阻尼系数的变化规律不同。

图3(c)表明:当惯容比小于最优值时,TID的附加最优模态阻尼比随着惯容比的增大而增大；当TID退化为SVMD后,斜拉索的最优附加模态阻尼比随着惯容比的增大而减小,最终稳定至VD为斜拉索提供的最大附加模态阻尼比。当惯容比接近临界值时,对斜拉索的附加最优模态阻尼比最大,即TID的最优惯容比接近其临界值。由图3可知:斜拉索前4阶模态获得的最大附加模态阻尼比基本相同,TID最优惯容比随着模态阶次的增大而减小,TID的最优频率比和阻尼比随着模态阶次的增大而增大。

3 TID对斜拉索减振控制的仿真分析

3.1 复模态分析结果验证

为验证复模态分析结果的适用性,以昂船洲大桥的某根斜拉索(参数见表1)为例开展了TID、VMD和VD对斜拉索减振控制的数值仿真分析。首先进行斜拉索-阻尼器耦合系统目标模态的稳态激励,待斜拉索振动响应达到一定值后,去除外激励,然后计算此时斜拉索的自由衰减振动响应。假定激励荷载为:

(20)

式中:k为斜拉索-阻尼器耦合系统的模态阶次；ωk为斜拉索-阻尼器耦合系统的第k阶模态的振动圆频率；ti为激励持续时间；H(ti-t)为单位阶跃函数，

(21)

表1 斜拉索主要参数值

基于MATLAB/Simulink工具箱,仿真时将斜拉索离散为200个均匀单元,且所有阻尼器安装位置距离斜拉索锚固端2%的斜拉索长度。

图4为TID惯容比μ等于0.5、阻尼比和频率比取为最优值时斜拉索第1阶模态稳态激振的跨中位移时程响应。采用指数函数拟合斜拉索自由衰减区段的位移峰值,识别得到的斜拉索附加模态阻尼比为2.67%,与复模态分析结果的2.678%吻合良好。

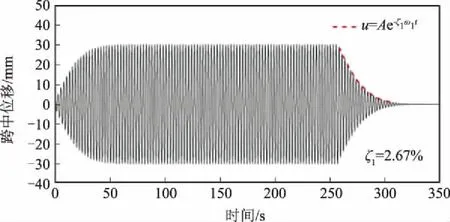
图4 斜拉索第1阶模态稳态激振跨中时程曲线(μ=0.5)

在此基础上,图5对比了斜拉索前两阶最优附加模态阻尼比的仿真和复模态分析结果发现,二者吻合良好。因此,可采用复模态分析进行TID对斜拉索附加模态阻尼比的计算。

图5 斜拉索最优附加模态阻尼比的复模态分析与仿真分析结果对比(xd/l=0.02)

3.2 TID、VMD和VD减振效果对比分析

图6对比了TID、VMD和VD控制时斜拉索第1阶模态的最优附加模态阻尼比,其中VMD的惯容系数的取值与TID的相同。

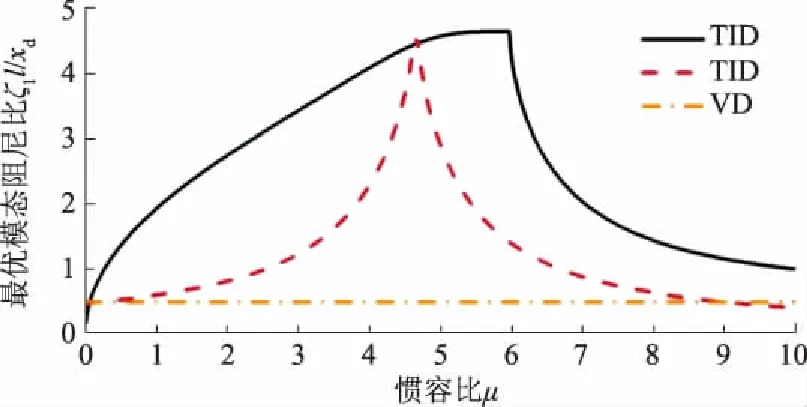
图6 TID、VMD和VD最优附加模态阻尼比对比

由图6可知:TID为斜拉索提供的附加模态阻尼比远大于相同惯容系数的VMD和最优控制的VD所提供的。此外,随着惯容比的增大,TID为斜拉索提供的附加模态阻尼比始终大于VD所提供的,而VMD惯容系数较大时可能会引起斜拉索减振效果的下降。综上,TID可以为斜拉索提供更高的附加模态阻尼比,且较大的惯容系数也不会引起斜拉索减振效果的严重下降。

图7为TID、VMD和VD为斜拉索第1阶模态提供的附加模态阻尼比随阻尼器阻尼系数变化的关系曲线,其中，TID的惯容比取为0.5,频率比取其最优值,VMD的惯容系数与TID的相同。

由图7可知:TID的阻尼系数远小于VMD和VD的,但其为斜拉索第1阶模态提供的附加模态阻尼比远大于VMD和VD的,表明在一定程度上采用TID减振是一种更加经济有效的斜拉索减振措施。

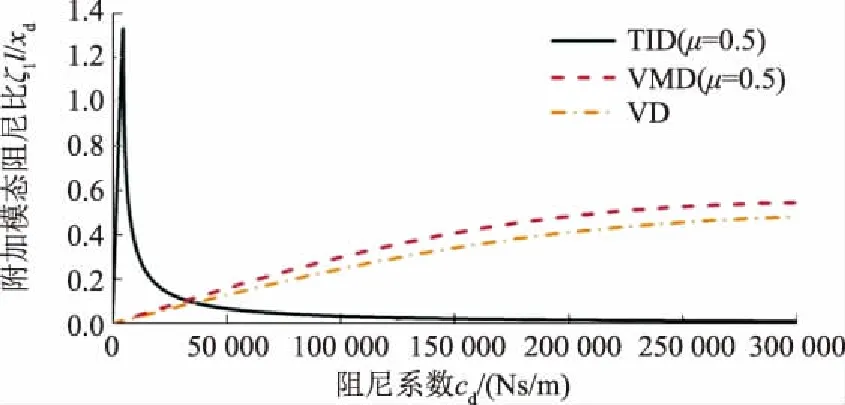
图7 TID、VMD和VD提供的斜拉索第1阶附加模态阻尼比随阻尼系数的变化关系

图8和图9分别为TID、VMD和VD最优控制对应的斜拉索第1阶模态稳态激振的跨中位移时程曲线和振动总能量。其中斜拉索的振动总能量由下式计算:

(22)

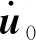
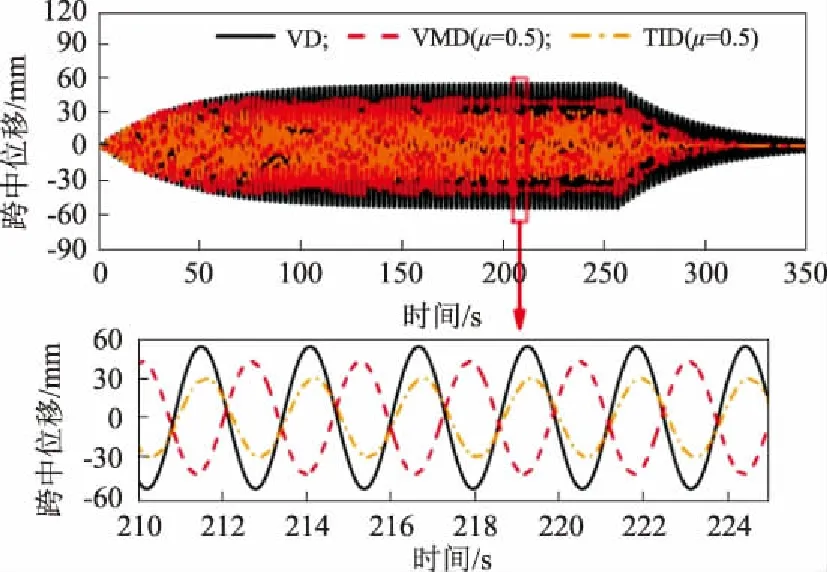
图8 斜拉索第1阶模态跨中时程对比

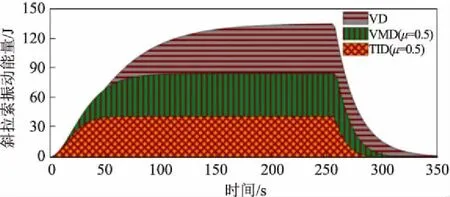
图9 斜拉索第1阶模态振动能量对比

结合图8和图9可知:在相同荷载激励下,与VD和VMD相比,TID能进一步降低斜拉索的稳态振动位移幅值和振动能量。

4 TID斜拉索减振控制增效机理

由于惯容单元和弹簧单元均不耗散能量,TID完全依赖于其阻尼元件耗能。TID阻尼单元在一个完整周期T内的耗能为：

(23)

式(23)表明:TID耗散的振动能量与阻尼元件的阻尼系数和运动速度均相关。为了同时考虑阻尼系数和阻尼元件运动速度对阻尼器耗能效率的贡献,引入参数φc表示阻尼器的耗能效率，

(24)

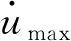
为探讨TID调谐作用对其耗能效率的影响,图10对比了TID阻尼系数相同时频率调谐和非调谐2种状态下TID的耗能效率时程曲线。由图10可见，频率调谐的TID的耗能效率幅值远大于相应失谐状态的。因此,TID卓越的减振性能主要在于内部调谐作用放大了阻尼单元的位移,提升了TID的整体耗能能力。

图10 TID频率失谐和调谐状态对应的耗能效率时程对比(μ=0.5)

5 结论

1)TID为斜拉索各阶模态提供的最大附加模态阻尼比基本相同,TID最优惯容比随着模态阶次的增大而减小,TID的最优频率比和阻尼比随着模态阶次的增大而增大。

2)与VMD和VD相比,TID可为斜拉索提供更高的附加模态阻尼比,并显著降低了斜拉索在相同荷载激励下的振动位移幅值和振动能量。

3)TID卓越的减振性能归功于调谐作用对内部阻尼元件位移的放大效应。