单值三角Neutrosophic交叉熵的TOPSIS方法
范建平,贾雪飞,吴美琴
山西大学 经济与管理学院,太原030006
1 引言
自从1965 年Zadeh[1]提出模糊集(Fuzzy Sets,FS)的概念之后,模糊集被广泛应用,但是Zadeh 提出模糊集仅仅使用隶属度这一个参数来表示决策信息的不确定性。Atanassov[2]在模糊集的基础上引入非隶属度,提出了直觉模糊集(Intuitionistic Fuzzy Set,IFS),可以有效地处理模糊集所不能处理的问题。Gargov 等人[3]和Atanassov 等人[4]将隶属度函数和非隶属度函数扩展到区间数,提出了区间直觉模糊集。然而在处理实际问题时,刻画模糊信息的隶属度可能会在几个值之间进行波动,为解决这个问题Torra[5]定义了犹豫模糊集(Hesitant Fuzzy Set,HFS)。Qian 等人[6]和Zhu 等人[7]在此基础上分别定义了广义犹豫模糊集和双重犹豫模糊集。但是,有时会出现隶属度与非隶属度之和大于1的情况,Yager[8]提出Pythagorean 模糊集来解决这一问题,允许隶属度与非隶属度之和大于1,同时需要满足隶属度与非隶属度的平方和小于等于1,Pythagorean 模糊集拓展了直觉模糊集能够处理的模糊性信息。尽管模糊集理论已经被广泛研究和拓展,但是模糊集及其拓展无法处理不连续和不一致的信息。例如,医生做出某种诊断的时候,认为这位患者60%是患这种疾病,但是又有50%可能是另一种疾病,同时还有20%的不确定性,这种情况无法用模糊集及其拓展集进行处理,所以就需要一些新的理论。Neutrosophic 集(Neutrosophic Set,NS)的出现刚好弥补了这一不足,Smarandache[9]提出Neutrosophic 集的概念,用真实值隶属函数,不确定性隶属函数和失真值隶属函数,即非标准单位区间]0-,1+[的集合来表示模糊信息,其中不确定性隶属函数不像直觉模糊集中的犹豫度与隶属度和非隶属度有关,这里的不确定性隶属函数、真实值隶属函数和失真值隶属函数彼此独立[13]。
Neutrosophic 集虽然扩大了不确定信息的表达方式,但是在实际应用中非常不方便,为了简化Neutrosophic集,Wang 等人[10]在Neutrosophic 集的实例上定义了集合理论算子(the set theoretic operators),并称之为单值Neutrosophic 集(Single Valued Neutrosophic Set,SVNS)。Ye[11]将单值Neutrosophic 集和区间Neutrosophic 集统称为简单Neutrosophic 集,并提出相应的集结算子和cosine相似度测量,将其运用到多准则决策(Multi-criteria Decision Making,MCDM)中。Peng 等人[12]对文献[11]中简单Neutrosophic 集中不合理的地方进行了改进,Peng 等人[13]基于直觉模糊集的得分函数提出了Neutro‐sophic 集相应的得分函数、精确函数和确定函数,并根据其对Neutrosophic 数(Neutrosophic Numbers,NN)的大小进行比较,这些在之后Neutrosophic 集的相关研究中被广泛使用。Ye[14]对文献[11]中的cosine 相似度测量公式进行改进。Majumdar 和Samanta[15]定义了单值Neutrosophic 集中相关的距离公式,并提出单值Neutro‐sophic 集的熵(Entropy)及相似度的测量。刘春芳和罗跃生[16]将区间Neutrosophic集中的熵和相似度应用于排序之中。Ye[17]在模糊集交叉熵(Cross Entropy)的基础上进行拓展,提出了单值Neutrosophic集的交叉熵,并将其运用到MCDM 中。Wu 和Wang[18]指出文献[17]中的交叉熵有缺陷,并据此提出两个新的交叉熵测度。Biswas、Pramanik 和Giri[19]将三角模糊数和单值Neutrosophic 集结合起来,研究了单值三角Neutrosophic 集及其在MCDM 中的应用,提出单值三角Neutrosophic 集的加权算术平均算子和加权几何平均算子用以聚合单值三角Neutrosophic 集。Deli[20]提出了单值三角Neutrosophic集(Single Valued Triangular Neutrosophic Set,SVTrNS)的截集和真实值隶属度、不确定性隶属度、失真值隶属度的模糊性,并据此给出了一种新的排序方法。Avishek 等人[21]定义了不同类型的线性和非线性广义三角Neutrosophic 数,同时给出了将Neutrosophic 数转化为精确数的方法。Abdelbasset 等人[22]分析了单值三角Neutrosophic 集的互反判断矩阵,并对群决策中的一致性问题进行处理。
Chen 等人[23]提出TOPSIS 方法,通过备选方案与正、负理想解之间的距离确定其排序。Smarandach 等人[24]将TOPSIS 方法进行简化,并将其应用于Neutro‐sophic 集中。Biswas 等人[25]将TOPSIS 方法应用于单值Neutrosophic 集中。Liang 等人[26]对TOPSIS 方法进行改进,并将其运用到语言Neutrosophic集中,用于评估金属矿山的投资风险。TOPSIS 方法需要用到决策信息的差异程度,但是采用距离公式测量会丢失掉一部分不确定信息,而交叉熵可以有效衡量决策信息的模糊性和准则之间的关联性,同时还可以消除距离测度的不利影响,比较适合测量不确定信息和不连续信息。
本文在单值三角Neutrosophic集环境中提出一种新的交叉熵测度,用新的交叉熵公式测量两个单值三角Neutrosophic 集之间的差异程度,并提出基于单值三角Neutrosophic交叉熵的TOPSIS方法。
2 相关概念
2.1 Neutrosophic集
定义1[9]令X 是一个对象(点)集,满足x ∈X。X上的Neutrosophic 集A是x 属于A的真实值隶属函数TA( x),不确定性隶属函数IA( x )和失真值隶属函数FA( x)组 成 ,是 ]0-,1+[ 中 的 非 标 准 子 集 ,即TA( x):X →]0-,1+[I,A( x):X →]0-,1+[,FA( x):X →]0-,1。+[由于TA( x)、IA( x)、FA( x )的和没有限制,因此满足:

Neutrosophic集A可记为:
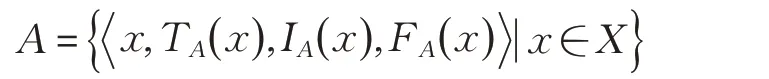
定义2[27]令X 是一个对象(点)集,满足x ∈X。TA( x)、IA( x)、FA( x )退化成[0,1]中的一个精确数时,则称 A 为 单 值 Neutrosophic 集 ,且 满 足0 ≤TA( x )+IA( x )+FA( x )≤3。为 方 便,称x=( T,I ,F)为 单 值Neutrosophic 数,其 中T,I,F ∈[ 0,1],并 且0 ≤T+I+F ≤3。
2.2 单值三角Neutrosophic集
定义3[28]将x 用三角模糊数表示,令μ,v,γ分 别 是 属 于[ 0,1 ]区 间 上 的 精 确 数,且a1,a2,a3∈R,a1≤a2≤a3,其中μ,v,γ分别表示最大真实值隶属度、最小不确定性隶属度和最小失真值隶属度。则一个单值三角Neutrosophic 数可以表示为其真实值隶属函数,不确定性隶属函数和失真值隶属函数如下:

定义4[29]设是两个单值三角Neutrosophic 数,则:
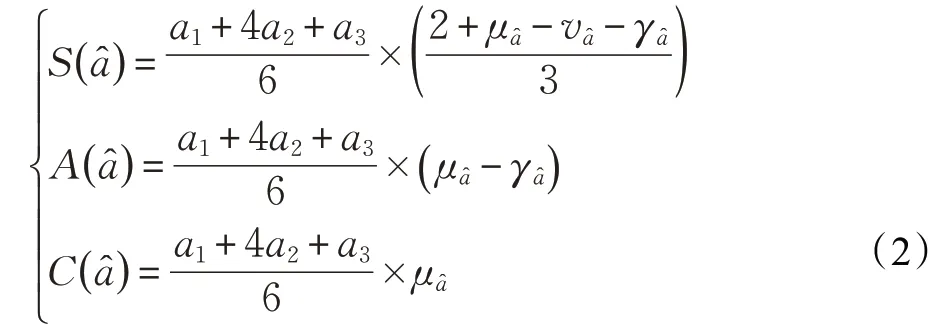
(3)运算[19]:
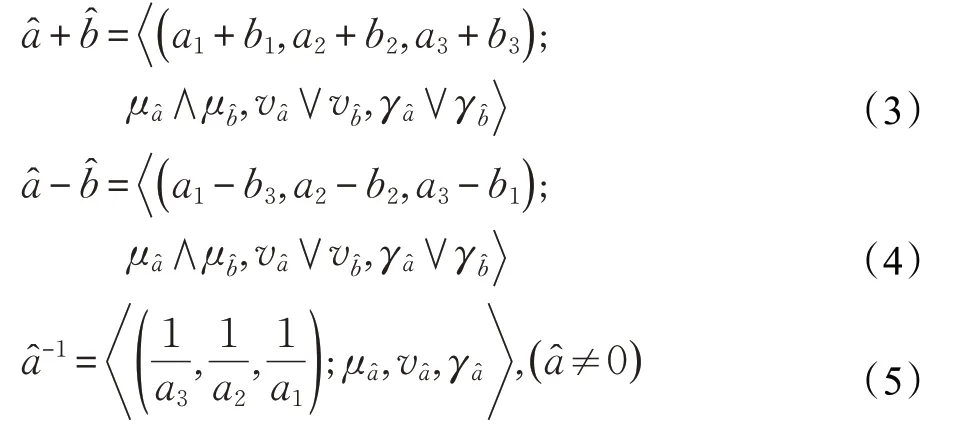

3 单值Neutrosophic交叉熵
3.1 交叉熵
定义5[30]设A、B 是两个模糊集,论域为X={x1, x2, …,xn},则A相对于B的交叉熵为:
基于模糊集交叉熵的定义,Ye[17]在此基础上进行拓展,提出了单值Neutrosophic集的交叉熵,并将其运用到MCDM 中。Wu 等[18]指出文献[17]中的交叉熵有缺陷,并据此提出两个新的交叉熵测度。设A、B是两个单值Neutrosophic集,则公式如下:

上述式子说明了A和B 之间的差异程度,即单值Neutrosophic 集中的差异信息,同时因为ISNS( A,B )无对称性,则A和B之间的对称差异信息测度可以表示为:
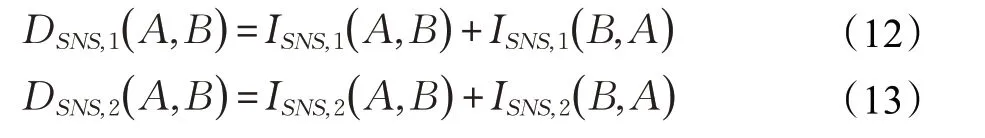
文献[18]中的两个新的交叉熵公式中存在不足,不能处理一些特殊的情况,如果假定δ=( 0,0 ,1 )是最小的单值Neutrosophic 数,在给定的单值Neutrosophic 数α和β 时,当α >β 时,α 与δ 的对称差异信息测度应该大于β与δ的对称差异信息测度,但是根据式(12)、(13)这两个交叉熵公式测量的结果刚好相反。正如例1所示:
例1令α=( 0.6 4,0,0.18),β=( 0.6 ,0.23,0.19 )是 两 个单值Neutrosophic 数,根据0.64>0.6,0<0.23,0.18<0.19,可得α >β,同时令δ=( 0,0 ,1) 是最小的单值Neutrosophic数,计 算得出DSNS,1( α,δ )=0.587 5,DSNS,1( β,δ )=1.956 9,DSNS,2( α,δ )=0.841 0,DSNS,2( β,δ )=0.843 5,即
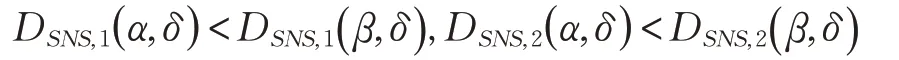
与理论不符,由于α >β,α与δ 的对称差异信息测度应该大于β 与δ 的对称差异信息测度,所以本文在此基础上对交叉熵公式中不合理的地方进行改进。
3.2 改进的交叉熵
为了克服这个不足,下面对单值Neutrosophic 集中的交叉熵公式中不足的地方进行改进。在证明改进交叉熵公式合理性的过程中,对定理的证明是必要的。
定义6设A、B是两个单值Neutrosophic 集,则A相对于B的交叉熵可以表示为:
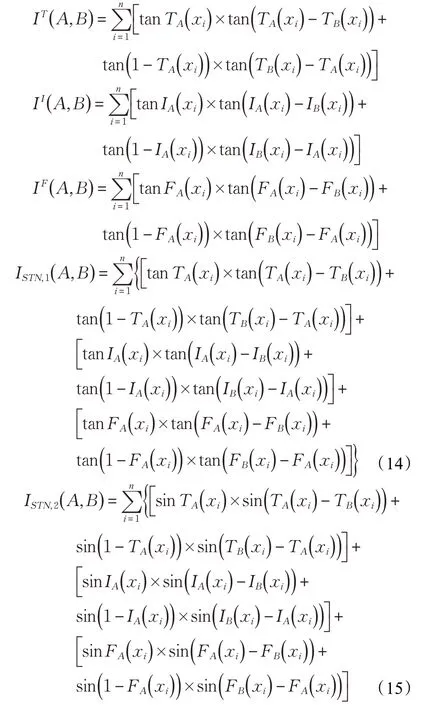
上述式子说明了A和B 之间的差异程度,即单值Neutrosophic集中的差异信息,同时因为ISTN( A,B )无对称性,则A和B之间的对称差异信息测度可以表示为:
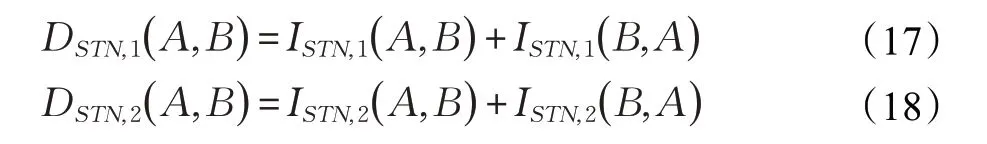
对称差异信息越大,表明A和B之间的差异程度也就越大。
据此,例1所出现的问题已经得到解决,假定δ=( )0,0,1是最小的单值Neutrosophic数,根据式(16)、(17)计算得出DSNS,1( α,δ )=4.056 3,DSNS,1( β,δ )=3,974 1,DSNS,2( α,δ )=1.667 7,DSNS,2( β,δ )=1.656 4 同时DSNS,1( α,δ )>DSNS,1( β,δ),DSNS,2( α,δ )>DSNS,2( β,δ)。满足在给定的单值Neutrosophic数α,β,当α >β 时,α与δ的对 称差异信息测度大于β 与δ的对称差异信息测度,根据本文改进后的交叉熵公式,文献[18]中交叉熵公式中不合理的地方已经得到解决,而改进后的交叉熵公式更加符合常理,适用于更多的情况。
假设A、B 是两个单值Neutrosophic 集,A、B 之间的对称差异信息测度为DSTN( )A,B,则下列定理成立:
(1)DSTN,1( A,B)=DSTN,1( B,A)DSTN,2( A,B)=DSTN,2( B,A)
(2)DSTN,1( A,B )≥0(DSTN,1( A,B)=0当且仅当A=B)DSTN,2( A,B )≥0(DSTN,2( A,B)=0当且仅当A=B)
(3)A、B之间的差异越大,则DSTN( A,B )就越大。
很明显就可以看出定理(1)是成立的,定理(2)、(3)的证明如下。
证明1已知
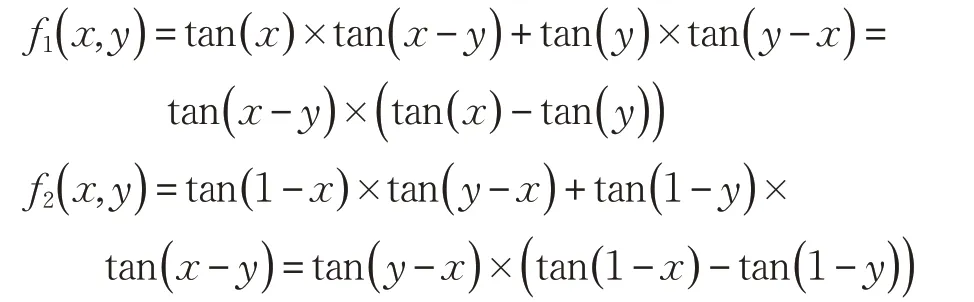
其 中,x,y ∈[ 0,1],不 论 是x ≥y 还 是x ≤y,都 有f1( x,y )≥0,f2( x,y )≥0 成立。那么A和B 之间的对称差异测度可以表示为:
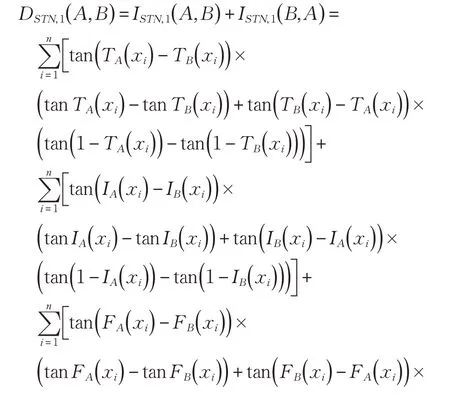

由于TA( xi)、TB( xi)、IA( xi)、IB( xi)、FA( xi)、FB( xi)都是[ 0,1 ]之间的精确数,根据f1( x,y )≥0,f2( x,y )≥0 可以得到:
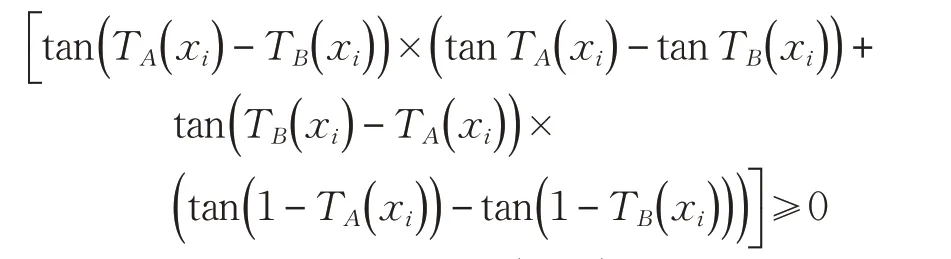
成立,进一步可以推导出DSTN,1( A,B )≥0 成立,当且仅当TA( xi)=TB( xi),IA( xi)=IB( xi),FA( xi)=FB( xi)时DSTN,1( A,B)=0 成立。
证明2A、B、C 是三个单值Neutrosophic 集,同时满足 A ≥B ≥C, 则 有 TA≥TB≥TC,IA≤IB≤IC,FA≤FB≤FC那么:
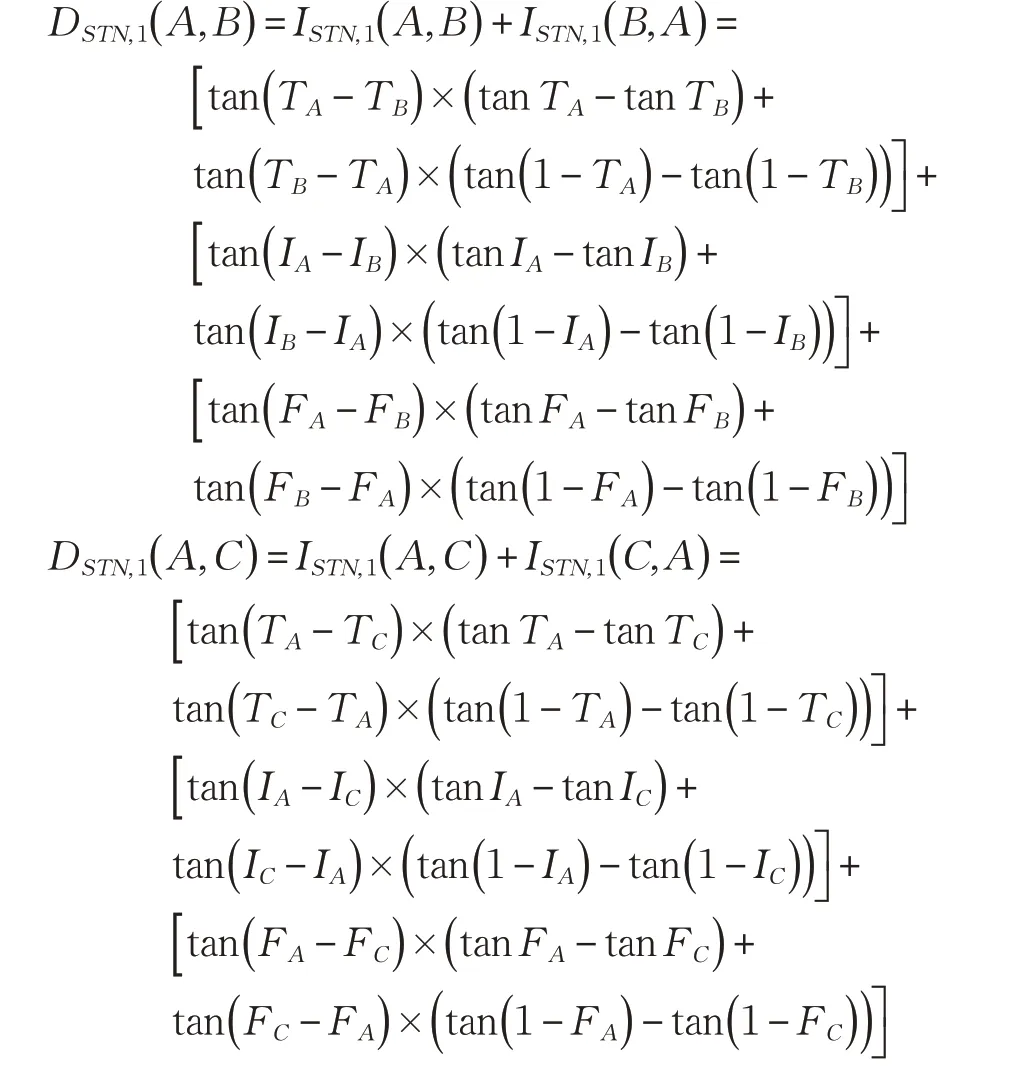
证明可得:

同理可证其他等式关系也成立,可得,DSTN,1( A,B )≤DSTN,1( A,C),DSTN,1( B,C )≤DSTN,1( A,C)都成立。同理可证,对于DSTN,2等式也成立。
定义7考虑到SVTrN-numbers具有的优势,将本文提出的单值Neutrosophic 集交叉熵引入到单值三角Neutrosophic集中,可得:
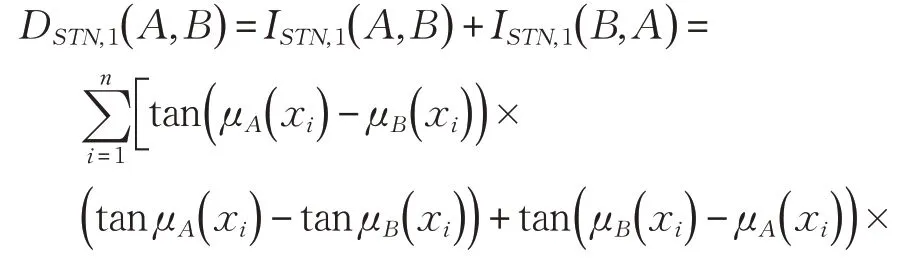
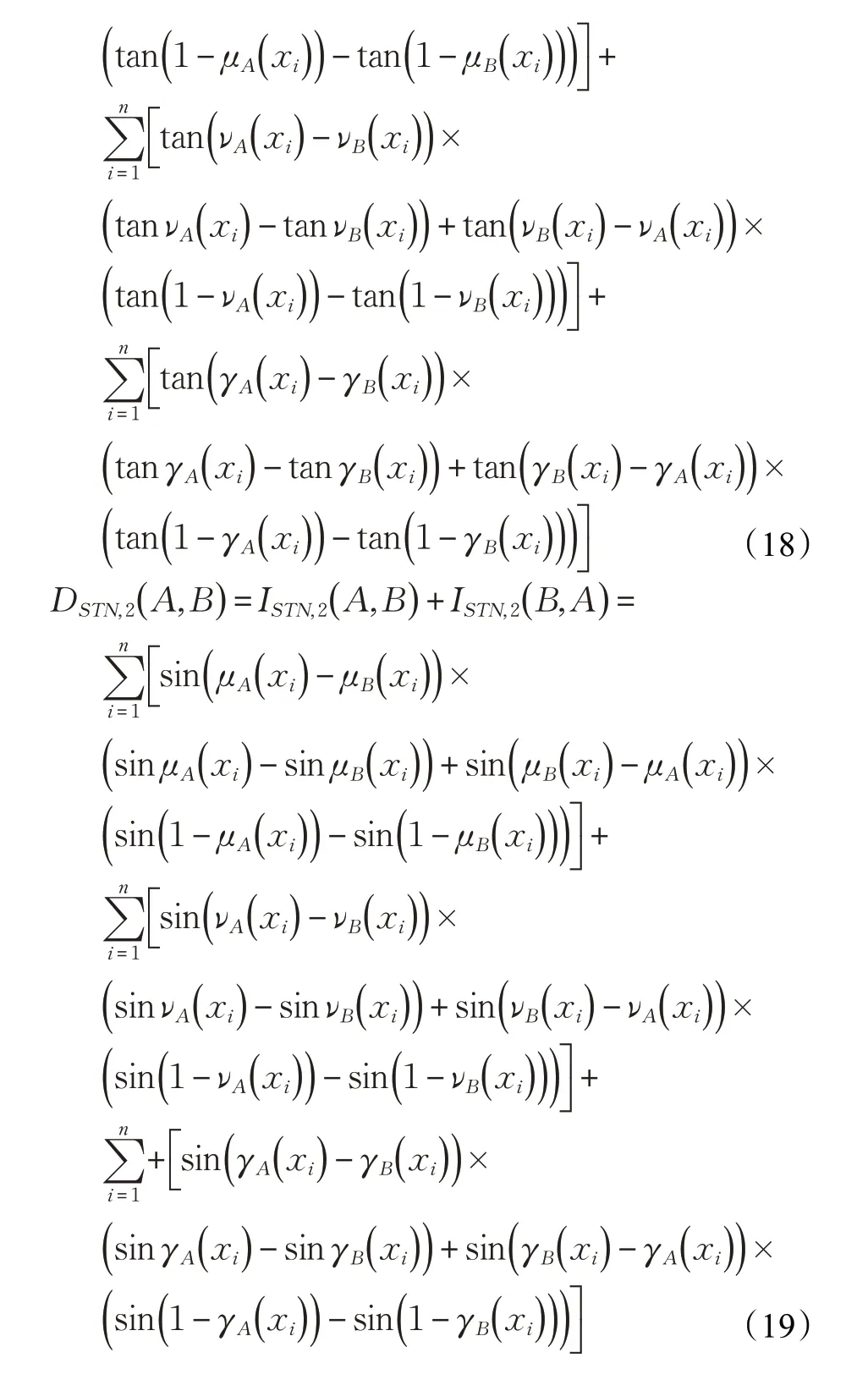
4 模型构建
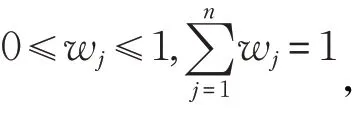
步骤1决策矩阵标准化
决策矩阵的信息必须进行标准化,只有标准化之后才可进行如下处理,标准化分为成本准则和效益准则,可以根据下列公式进行处理[8]:
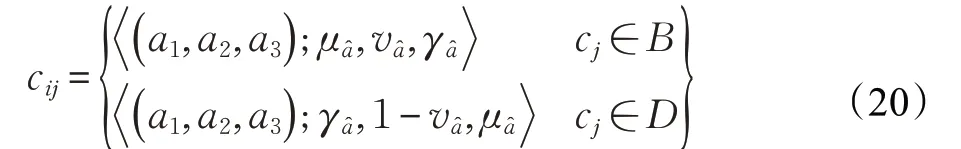
B、D分别为效益准则集和成本准则集。
步骤2计算正、负理想解
在单值三角Neutrosophic 环境下,根据三角Neutro‐sophic数的大小关系定义其正理想解和负理想解:
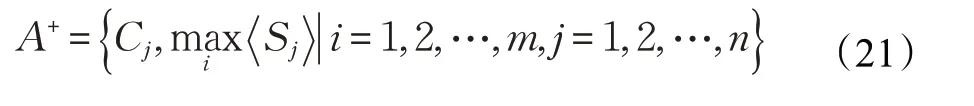

表1 决策矩阵

步骤3根据式(18)和式(19)分别计算备选方案与正、负理想解之间的交叉熵,交叉熵是用来衡量不同方案之间的对称差异信息测度,本文在这里用交叉熵来替代备选方案与正负理想解的距离,因为采用距离公式会丢失掉一部分不确定信息,而交叉熵可以有效地衡量信息的模糊性和准则之间的关联性,同时还可以消除距离测度的不利影响,比较适合测量不确定信息和不连续信息。
步骤4计算相对贴近度
通过式(18)和式(19)可得出不同方案的对称差异信息测度,根据其对称差异信息测度,确定相对贴近度,公式如下:
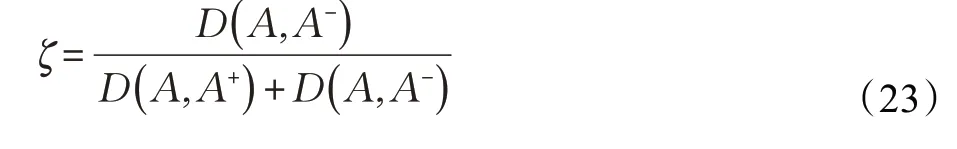
步骤5排序
根据相对贴近系数的大小对方案进行排序。ζ 的值越大,则方案越接近于正理想解,同时越远离负理想解;反之亦然。
5 算例分析
算例是一个医疗代表选择的问题,药房公司想选择一名医疗代表,现有5 个备选者X={ x1, x2,x3,x4,x5},有三个准则C={c1,c2,c3},分别代表的是口头沟通的技巧、从业的能力和自信程度,准则权重为W={0.3 ,0.3,0.4}T以此来选择出最适合的医疗代表。表1 是决策矩阵D={dij},i=1,2,3,4,5,j=1,2,3,表内的每一个数都是单值三角Neutrosophic 数,表示的是每个备选者在相应准则下的评估值。
步骤1决策矩阵标准化
由于本案例中的三个准则C={c1,c2,c3},分别代表的是口头沟通的技巧、从业的能力和自信程度都是效益准则,不用进行变更。
步骤2计算正、负理想解
根据式(21)和式(22)计算正、负理想解,结果如下:


表2 由DSTN,1 得到的结果
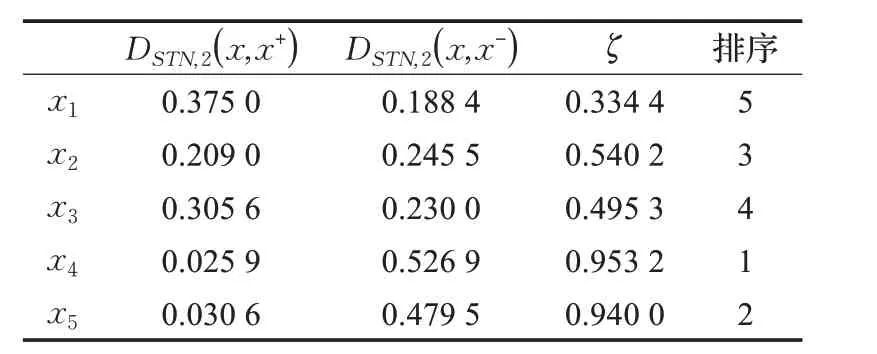
表3 由DSTN,2 得到的结果
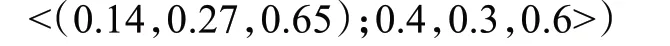
步骤3计算备选方案与正、负理想解之间的交叉熵
根据DSTN,1分别计算出方案与正、负理想解的对称差异信息测度及其排序情况如表2所示。
根据DSTN,2分别计算出方案与正、负理想解的对称差异信息测度及其排序情况如表3所示。
步骤4计算相对贴近度
由式(23)分别计算各个方案的相对贴近度,结果见表2和表3。

表4 对于不同方法的结果
步骤5排序
根据相对贴近度选出最适合的医疗代表,不论是表 2,还是表 3,相应的排序结果都为:x4≻x5≻x2≻x3≻x1,最适合的是x4,最不适合的是x1。
表4 是本文的方法与现有的不同方法之间比较的结果。
表4 是基于不同文献的对称差异信息测度公式,结合TOPSIS方法,根据相对贴近度计算得出的排序结果,本文的排序与已有方法的排序结果相比较,最适合的人选都是x4,其他人选的排序结果略有偏差,但是本文的两个交叉熵公式的排序结果是一样的,验证了本文改进交叉熵公式的稳定性。
6 结语
单值三角Neutrosophic 集相对于三角模糊数和单值Neutro‐sophic 集,拥有更多的不确定信息,因此也就能解决三角模糊数和单值Neutrosophic 集单个所不能解决的问题。本文的主要贡献:将交叉熵测度引入到单值三角Neutrosophic 集环境中,并对文献[18]中有关交叉熵公式中不合理的地方进行改进,提出新的交叉熵公式,使其适用于更多的情况,并将新的交叉熵公式和TOPSIS方法进行结合,用于MCDM中。
在未来,由于区间Neutrosophic 集和单值Neutrosophic 集统称为简单Neutrosophic 集,可以试着将三角模糊数引入到区间Neutrosophic集中,同时还可以对交叉熵公式的不同形式进行完善和证明。

