区间规划下的高残值易逝品供应链网络设计

陈 勇，杨雅斌

1.佛山职业技术学院 工商管理学院，广东 佛山528137

2.广州工商学院 物流系，广州510850

1 引言

随着信息技术的发展和普及，企业为了争夺市场份额往往会在新产品上市不久后就投入巨资研发下一代产品，这样就极大地缩短了产品的生命周期，尤其是电子类消费品和高科技产品。这些产品市场价值消逝极快但核心部件仍然具有较高的使用价值，称之为高残值易逝品。因此，为了及时充分挖掘这些产品的剩余价值，企业需要加快产品的回收并进行高效处理。许多企业为了尽快将这类产品在生命周期内销售出去，往往设法开拓电商销售渠道。同时，对高残值易逝品回收处理再利用可以为企业和社会带来显著的品牌和环保效应。

进入21 世纪，随着循环经济理念的发展，大量学者针对再制造闭环供应链进行研究，主要研究工作集中在四方面：闭环供应链的定价[1-3]、闭环供应链的回收渠道[4-6]、传统闭环供应链网络设计[7-9]，以及考虑碳排放的闭环供应链环保问题[10-12]。姚卫新考虑正、逆向物流以及电子商务对供应链的影响，构建一个包含正、反向的闭环供应链物流网络成本模型[13]。陈娟认为再制造闭环供应链的实施会产生潜在的经济收益，构建了一个单、双渠道下的正向和反向供应链模型，仿真结果表明产品的销售率和回收速度对经济收益有影响[14]。张桂涛等提出一个由供应商、制造商、零售商组成的三级网络模型；其中，制造商的产品通过线上线下渠道销售给消费者，产品被使用后产生的废旧品经由回收中心处理送往制造商重新再制造的闭环供应链网络均衡模型[15]。卢荣花基于产品生命周期理论研究只包含制造商和零售商两个决策主体的闭环供应链，建立了两周期的分散决策模型，结果表明：二者应根据不同的成本节约额制定不同的批发价、零售价和生产量[16]。于春海等设计只包含制造商和零售商两个决策主体的双渠道供应链结构，将销售期分为两个销售阶段，运用博弈论建立决策模型，并引入改进的收益共享契约有效解决渠道冲突问题[17]。李晓婧等将碳交易和碳排放纳入碳管理中，考虑原料的使用率和政府约束的再制造率，建立一个包含供应商、制造商、销售商、消费者和回收中心的双渠道闭环供应链网络均衡模型[18]。

以上文献的研究对象大多数集中在普通制造品上，很少研究高残值易逝性产品。许多学者在设计闭环供应链网络时考虑的因素不全面，尤其是没有考虑企业所掌握的已有信息，而片面地给产品需求量做一个单一假设。现实中，制造企业开发的新产品往往可分为大众消费者喜爱的产品和经常更新换代的产品。前者由于每年的销量稳定，新产品只是对旧产品的局部功能做简单改良而不完全颠覆，因而其回收量数据可以用一个区间数估计；而后者是为了满足特定的人群，其产品更频率高，因而这部分需求很难通过一个区间数来描述，此时，回收量采用一个随机参数估计比较有意义。因此，为了快速获取高残值易逝性产品的价值，在设计此类产品的闭环供应链网络时必须综合考虑高残值易逝性产品的回收点，回收成本与回收时间的关系，新、旧产品定价，以及回收量的不确定性。

在供应链网络规划中，一般都采取随机、模糊和区间等方式来描述事件的不确定性，并据此做出有利决策；然而采用前两种方法对不确定性问题进行优化时，需要知道参变量的相应函数关系，而实际上要获取这些分布函数并不容易[19]。但用区间数来表示参数的波动范围是很容易做到的，尤其在参变量分布未知的情况下，采用区间规划简单实用，产生的区间解可为决策者缩短决策范围。本文基于高残值易逝品的生命周期理论，考虑回收时间的价值性，以网络收益最大化为目标，建立了区间机会约束环境下的多产品、多周期、多渠道的闭环供应链网络模型。

2 模型建立

2.1 问题描述及假设

本文描绘的再制造闭环供应链网络结构由制造/再制造商、中间商、消费区、回收中心组成，如图1 所示。当新一代产品被研发出来后，制造/再制造商为了快速抢占市场，将新产品大规模地布局到中间商，中间商则快速地销往传统消费区（一级消费区）。为了降低企业的制造成本并承担起社会责任，制造企业将对这些高残值易逝性产品进行定期回收，回收源主要来自传统消费区使用过的旧品和中间商处的滞销品。对于没有质量问题的产品则可以在电商市场和二级市场进行二次销售，而对于没有直接销售价值但其核心部件仍然完好无损的产品则经过回收中心处理后直接运往制造/再制造商处，进行下一代产品的再制造处理。

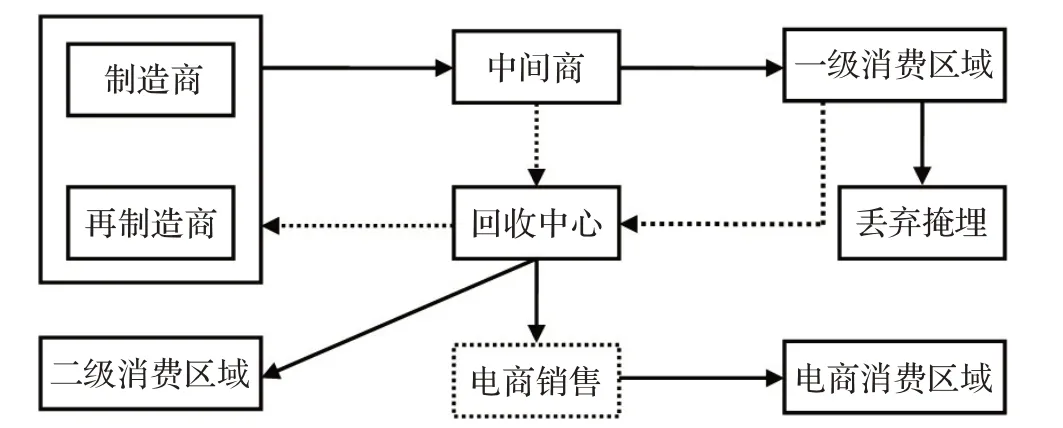
图1 基于电商环境下的高残值易逝品闭环供应链网络结构

在图1 构造的网络中包含诸多不确定性因子，主要是区间参变量和随机参变量这两类。为了有效地处理这两类参变量，本文拟采用区间规划和随机规划进行确定性转换。企业根据以往的销售历史数据可得到二手市场的产品需求分布函数，充分利用了其信息价值；同时该需求函数不能确保百分之百满足所有的约束条件，即它存在违背约束条件的风险，因而这部分需求采用机会约束方法描述较合理；对于产品的回收质量、回收成本、电商市场需求以及各个设施的处理能力等参数很难获取其分布信息，可以用区间表示这些不确定参数。

根据问题描述，在建立模型之前，给出以下假设：

假设新部件和再制造部件给消费者带来的产品效用都是一致的，不考虑产成品和零部件丢弃掩埋的处理成本，并且中间商滞留的合格产品不存在货损；产品生命周期包含成长期、成熟期和衰退期三个阶段，制造商对产品进行回收，产品回收时间发生在各阶段的末期。制造商在每一阶段的回收点如图2所示。

图2 产品在生命周期中的回收点

在成长期和成熟期末，对回收来的产品进行质量诊断和分类，对于不影响二次销售的产品则输出到电商消费区域与新产品同时销售，对于一些功能良好，只需要稍加维修、清洁就能将再利用的产品销往到二手市场；对于功能完全受损的产品则运回到制造/再制造商进行下一代产品的制造；在衰退期末，产品在三个阶段内结束销售后，便向一级消费区和中间商回收废旧品和滞销品，所有产品不再作质量诊断划分全部被运往制造/再制造商处进行再制造，而不再重新销往消费区域，以避免与新一代产品产生冲突。

当销往电商和二手市场的产品存在缺货时，需要承担相应的违约成本。其他假设如下：

假设1回收率和产品回收价格成线性关系[20]，则有方程：

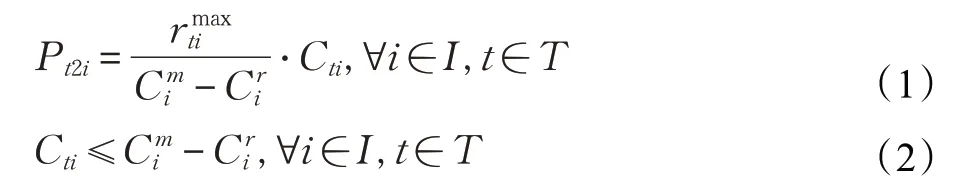
假设2产品的回收时间长短与处理成本大小成反比关系[14]，可采用成本-努力函数来表示产品的回收时间和处理成本的关系，其中，b为努力成本系数，ρ为努力强度。则有方程：

其中，CDti和CCti分别表示t 阶段从中间商处和一级消费区回收一单位产品i 所需要的收集处理费，包括产品的储存费和配送费；c 与cc分别表示从中间商和一级消费区回收的单位产品进行质量等级划分所需的固定处理成本，hti与mti分别表示t 阶段产品i 从中间商和一级消费区回收所需的时间；根据假设，有bc≥b,cc≥c。

假设3产品的市场淘汰率是恒定的，产品的生命长度与滞销率的关系[21]：

其中，Lti表示t 阶段产品i的生命长度，f( Lti)i表示Lti的函数。由此可知，产品的滞销率跟生命周期长度有关，如果产品的生命周期趋于∞，该产品不存在滞销。

假设4产品的价值随着时间的推移在不断地下降，具体表现在其价格的下跌[22]。假设回收的产品在电商消费区、二级消费区以及回收用于下一代零部件再制造的时间折现因子分别是ηn、ηm、ηng,ω(0 ＜ω ＜1)为价格系数，则t 时刻的销售价格可表示为：

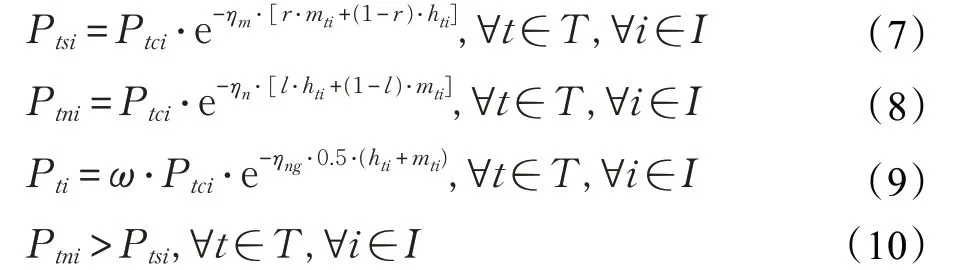
其中，Ptci表示t 阶段新产品i 的销售价格，Ptsi、Ptni、Pti分别表示t 阶段产品i在二级消费市场、电商消费区域以及废旧品、滞销品所回收的零部件用于下一代新产品再制造的销售价格，其价格与新产品的售价、中间商回收时间、一级消费区回收时间有关；为避免渠道竞争，假设回收的产品销售到二手市场的价格要低于电商市场的价格，同理可得电商市场的价格要低于新产品的售价。

假设5产品从中间商和一级消费区域的回收时间不能超过该类产品下一阶段的时间长度。随着产品更新换代速度加快，衰退期末产品的回收时间必然要小于下一代新产品的成长期，而下一代新产品相对于上一代产品的各阶段长度将明显缩小。因此，衰退期末的产品回收时间要小于本代产品的成长期。

2.2 模型参数与决策变量

2.2.1 下标

I：制造/再制造产品类别的集合，i ∈I;J：中间商的集合，j ∈J;K：一级消费区域集合，k ∈K;V：回收处理中心的集合，v ∈V;T：生命周期阶段的集合，t ∈T。

2.2.2 决策变量

2.2.3 参数

（1）能力约束

（2）比率量

（3）费用

（4）收益

2.3 目标函数

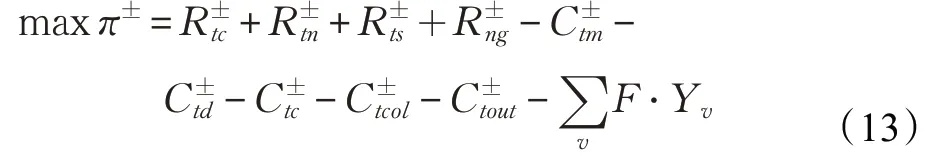
（1）各渠道的销售收入，包括正向供应链在传统市场的销售收入、逆向供应链在二级/电商市场的再销售收入以及零部件用于下一代产品再制造的销售收入。

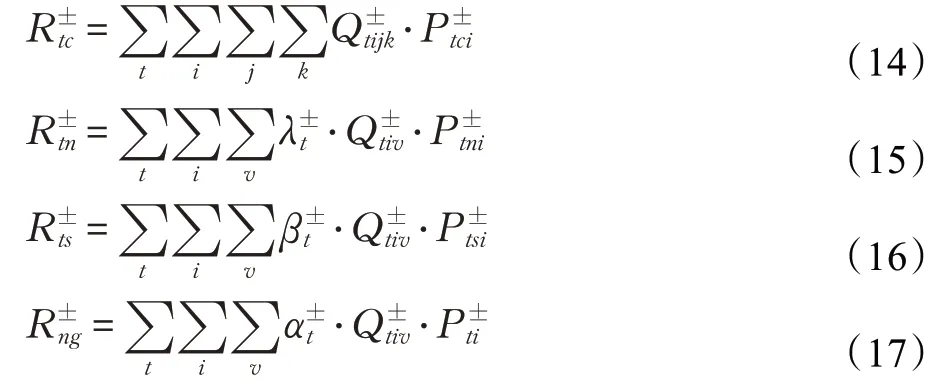
（2）各供应链成员的成本，主要包括制造/再制造商、中间商、一级消费区域、回收中心、再销售过程等发生的费用。

约束条件：

（1）流量守恒：分别表示制造/再制造商、回收中心、中间商、一级消费区的流量平衡。

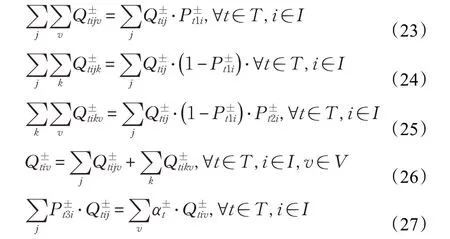
（2）能力约束：分别表示制造/再制造商、中间商、回收中心的最大服务能力限制。

（3）回收中心选址约束：回收中心选址属于二元事件，用0-1规划表示，Z 表示备选回收中心的数量。

（4）再销售需求约束：二级消费区域和电商消费区域对产品的需求量约束。

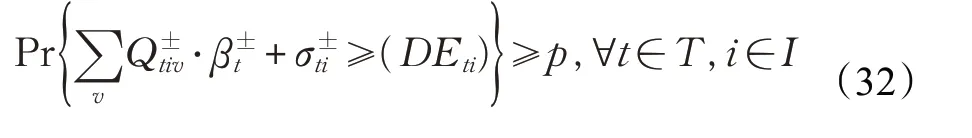
（5）其他约束：对于网络模型而言，各参数及变量应为非负的。

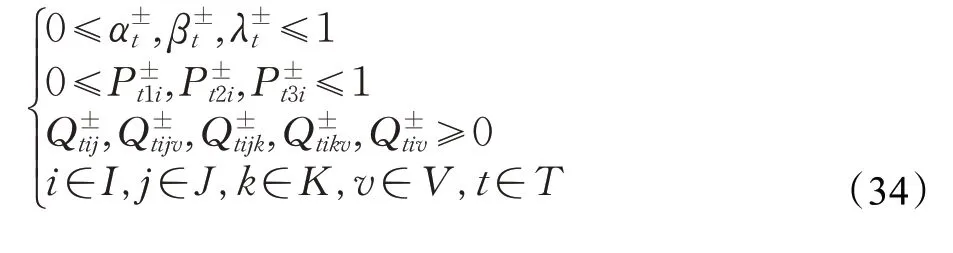
2.4 确定性转化

在数学规划中，根据实际问题所建立的数学模型，如果只考虑部分变量取为整数值，则称为混合整数规划。在区间规划的基础上融合混合整数规划方法形成区间混合整数规划（Interval Mathematical Linear Programming，IMLP），用于解决模型中含有整数决策变量的区间不确定性的数学规划问题。区间混合整数规划的一般形式如下：

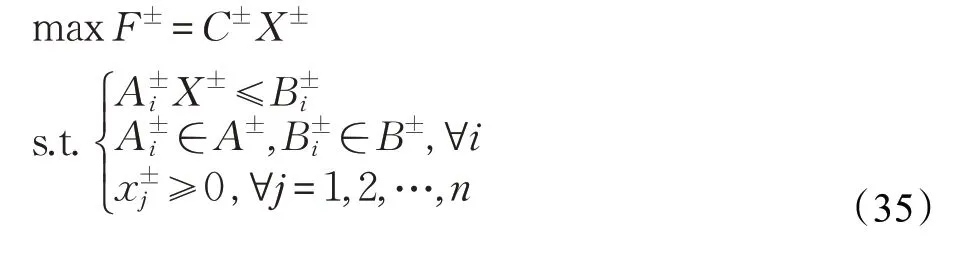
对于区间整数规划的转化，可参照Huang[23]利用特定的相互作用的两阶段法去求解区间模型，即如果目标函数是要求最大化的话，则先模拟对应上限的子模型(f+)并进行求解，然后根据上限模型求得的解，模拟求解下限子模型(f-)，最后对两个子模型所求的解进行合并得到一个区间值。上限子模型的形式如下：

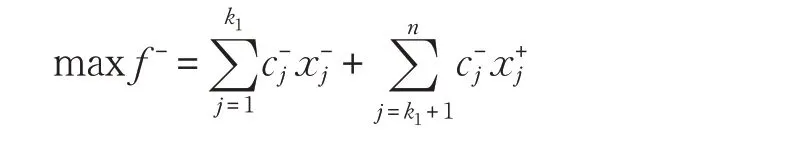
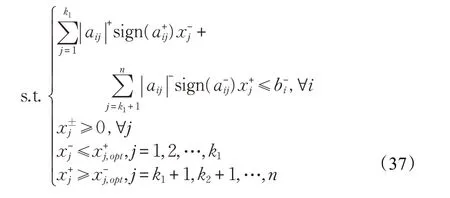
机会约束规划对每个约束i都有一个确定的概率水平pi，同时需要保证每个约束条件至少在pi的概率水平上成立。一般地，机会约束规划的不确定性能够分别表现在模型的目标函数和约束条件中。机会约束规划转化如下：

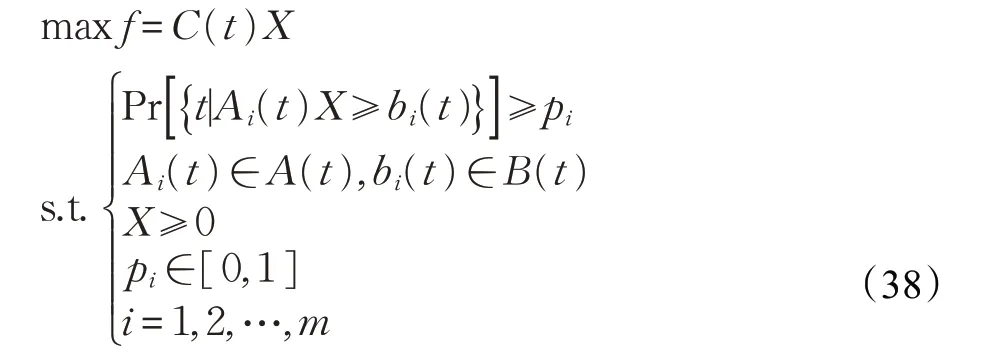
若A是确定的，B是随机变量，B的累积分布函数为F(bi),bi(t)pi=F-1(pi)，则根据随机变量累积分布函数的定义可知：

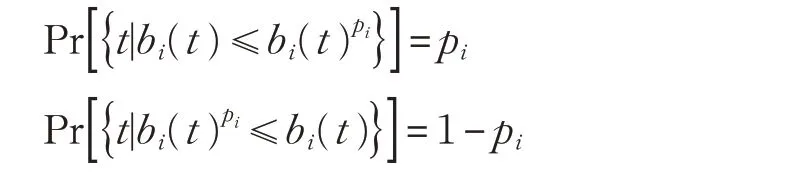
若 AiX=bi(t)pi, 则 Pr[ {t |AiX ≥bi(t)} ]=；piAiX ≥bi(t)pPi,r[ {t |AiX ≥bi(t)} ]≥p，i由 此 可 知AiX ≥bi(t)pi等价于Pr[{t|AiX ≥ bi( t)} ]≥p。i初始问题等价转化为：

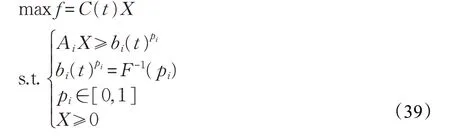
通过以上确定性方法转化，利用Lingo 编程求解可以获得目标函数π±、滞销率、回收率、再制造率、电商售价、二手市场售价、零部件的售价以及从中间商、一级消费区域回收产品的时间等的最优解。

3 算例描述与求解

3.1 算例描述

已知某高残值易逝性产品的生命周期包括3 个阶段，其闭环供应链网络结构由1个制造/再制造商、3个中间商、4个一级消费区、1个二级消费区、1个电商消费区和3个备选回收中心构成。产品1、2在一级消费市场的售价分别为2 500 元、3 500 元；制造商到中间商的单位产品运费为0.003元/km；中间商到所有一级消费区和回收中心的运费都为0.005 元/（km·件）；一级消费区到所有回收中心的运费为0.004 元/（km·件）；回收中心到制造/再制造商和二级消费区的运费为0.003 元/（km·件）和0.004 元/（km·件）；电商销售的运输成本为15 元/件。3个周期阶段下产品1的回收率为0.7、0.6、0.5，产品2的回收率为0.8、0.7、0.6。备选回收中心1、2、3的固定投资成 本 依 次 为550 000 元、520 000 元 和500 000 元；

cc=50,c=25,b=0.6,bc=0.8,ηn=0.4,ηng=0.5,ω=0.15,r=0.6,l=0.65,ηm=0.42。周期长度和需求信息如下：

（1）周期长度

表1 产品在各个生命周期阶段的回收成本和周期长度

（2）需求信息

假设至少满足二级消费区域不缺货的概率p 为0.95，而对于二级消费区域下的产品需求可以通过已有数据来模拟生成需求分布函数，假设该消费区的需求量服从正态分布函数。成熟期，二级消费区对产品1、2 的需求分布函数分别为N(220,302)，N(150,282)；电商市场在成长期和成熟期对产品1 的需求为[300，350]、[200，250]，对产品2的需求为[250，300]、[150，200]。

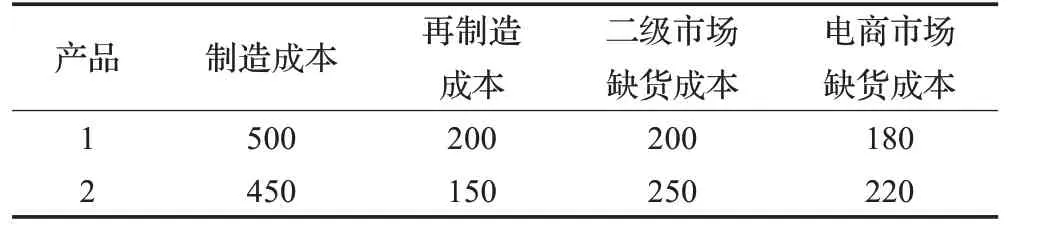
表2 产品的制造/再制造成本及市场的缺货成本（元/件）

表3 产品i在中间商j和备选回收中心v的库存费用 元

（3）其他参数

产品的各项成本费用、可再利用率、设施间的距离和服务能力约束如表1至表7所示。

表4 中间商j到制造/再制造商、一级消费区域k以及备选回收中心v的距离km

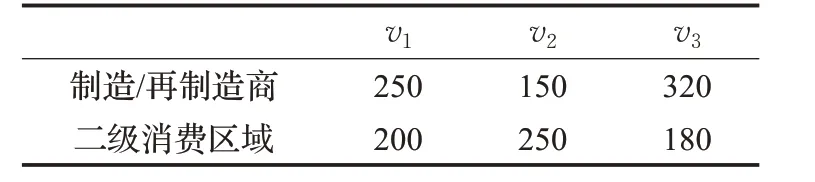
表5 制造/再制造商、二级消费区域到备选回收中心v的运距km

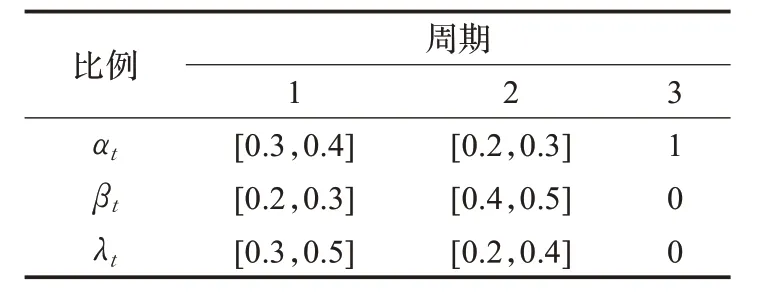
表6 经回收中心加工后，流入各个市场的产品分布比例

表7 制造/再制造商、中间商和回收中心的服务能力约束

3.2 算例求解

根据以上数据，取p=0.95，在CPU Intel®CoreTMi5-7500为3.40 Hz、内存为8.00 GB运行环境下，采取总耗时2 s，经过884步迭代，得到最大利润区间为[21 086 910，25 716 790]，Y1=[1,0],Y2=1,Y3=[0,1]，模型的其他解见表8。

企业最大利润的平均值为23 401 850 元，偏差为2 314 940元，偏差率为9.9%。在网络优化的过程中，回收中心的选址是重点考虑的内容，通过分析可知，在2号备选地必须建立回收中心，而1 号备选地在求最小目标值时需要进行考虑，在求最大目标值时，应考虑3 号备选地；企业应该结合自己的战略定位考虑是否对1、3号备选地建设回收中心：比如，采取收缩性战略的企业急需回笼资金，减少固定资产投资，因而可以选择固定投资成本较小的3 号回收中心；若处于扩张型战略的企业，追求市场占有率是其首要目的，因此，应当考虑在回收处理能力较大的1号备选地设立回收中心。

根据产品所处不同生命周期，其表现出的网络不确定性也不一致，由表8 结果可知，通过比较各参数的总体偏差率发现，衰退期的产品最稳定。通过比较又可发现产品1各项参数的波动较产品2大。产品的价格与回收时间密切相关，回收时间不确定性越大，造成的产品价格偏差较大。如产品1 在成熟期的中间商回收时间为[0.097，1.48]，其销往再制造厂的价格为[182，345]，偏差率达到30.93%。产品1 在成长期和成熟期存在缺货风险，在成熟期，产品1 销往二级消费区缺货量为57，销往电商消费区缺货量为[67，83]；在成长期，产品1 销往电商消费区的缺货量为[100，117]。

表8 区间机会约束方法下不同阶段各决策变量最优解

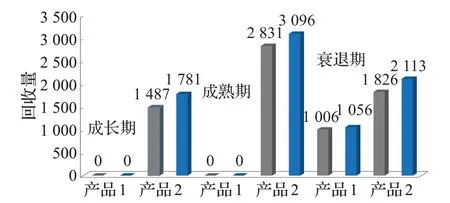
图3 产品1和产品2在回收中心的流量

三个阶段下，两种产品经过回收中心的流量如图3所示，灰色立体柱代表最低流量值，蓝色立体柱代表最高流量值。由图可知，由于产品1 在二级市场和电商市场均存在缺货情况，所以产品1 在这两个阶段没有回收量，产品1 在衰退期的回收量为[1 006，1 056]。由于产品2的制造和再制造成本比产品1低，加之其残值较高，导致产品2 在二级市场和电商市场的销量比产品1 高，所以在每一阶段中，产品2的回收量都会高于产品1。

综上，企业应该重点关注产品1 的回收时间和缺货量，根据产品1 在市场的销售情况和库存水平，应该缩短产品1 的回收时间，适当提高二级市场和电商市场的价格，同时加大产品2 的投入生产，发挥回收中心的作用。受篇幅限制，其余各个节点的流量不再赘述。

为了检验模型的稳定性，将置信水平p 分别取0.95，0.85，0.75，0.65，0.55 时，所得的最优选址决策方案和目标函数值如表9 所示。由结果表明，网络选址决策不受p值影响，证明该模型具有稳健性。当至少满足二手市场不缺货的概率越大时，企业所需承担的风险就越小；即随着p值增大，企业获得的利润就越大，但增幅甚微。因此，企业在缺货的情况下所承担的缺货成本比较小，可以考虑提高产品的价格，从而获取更多的利润。

表9 置信概率p对目标值和决策点的影响

4 结束语

本文针对高残值易逝性产品的特性，基于产品生命周期理论建立了双渠道环境下的再制造闭环供应链网络模型。该模型主要创新点是分析产品从各个渠道的回收时间和产品所处的生命周期长度之间的关系，最终目的是减少产品从其他渠道的回收时间，极大地利用产品的剩余价值。对于模型中的不确定性参数，采取了区间机会约束混合整数规划方法进行不确定性转化，数值仿真所得的结果可以为企业在设施选址、产品定价、产品回收时间、产品销量等提供决策依据。最后通过分析不同置信水平条件下的目标值，验证了该模型的稳健性。

本文将中间商和回收中心分开来考虑，下一步研究则可以将二者合并成一个主体，在环保理念和制造商返利的诱导下，中间商将主动承担产品回收，从而构建一个新的闭环供应链网络。区间规划理论应用于闭环供应链网络求解的案例比较多，该方法虽然简单可行，但是所得的区间解若是太大，则对决策者没有参考价值，因此下一步研究需要给区间设定一个度，即决策者在可承受的区间范围内所做的决策。